Математические методы параметрических прогнозных исследований

Такого рода прогнозные и плановые исследования чаще проводят при ситуационном и социально-этическом методе в системе управления.

Прогнозная экстраполяция (пролонгация процессов) применяется, если время упреждения укладывается в рамках эволюционного цикла.

Параметрические методы исследования можно применять тогда, когда за время упреждения не изменяются ни функции, ни структура объекта прогнозирования.

При возникновении в рамках времени упреждения прогноза или плана скачка в развитии объекта, изменении функций или структуры используют интуитивные или функционально-логические методы. Методы прогнозной экстраполяции оперируют с количественной информацией. Они хорошо разработаны/8, 9/. Чаще всего вычисления в соответствии с этими методами включены в резидентное программное обеспечение современных вычислительных средств. Поэтому основная задача настоящего раздела книги - ознакомить прогнозиста-пользователя современных вычислительных средств и программных продуктов:

1) с объемом информации о системе управления, необходимой для их применения;

2) с принципами, лежащими в основе этих методов;

3) с основными ограничениями на их применение.

На применение математических методов прогнозирования в условиях переходной экономики существуют достаточно жесткие ограничения. Эти ограничения связаны со следующими обстоятельствами:

1. Математические методы прогнозирования применяются, если величина времени (глубины) упреждения укладывается в рамках одного из циклов объекта прогнозирования /7/. Глубину прогноза (плана) определяют, как отношение абсолютного времени упреждения к величине соответствующего цикла объекта прогнозирования. При возникновении в рамках времени упреждения скачка в развитии объекта прогнозирования рекомендуется использовать интуитивные методы для определения силы скачка и времени его осуществления.

2. Каждый из статистических методов имеет довольно жесткие требования к качеству обрабатываемых данных (напри-

мер, к их однородности) и гипотезам о характере поведения анализируемых величин (их распределений) /8/. Нужно учитывать, что на практике исследователь, прогнозист имеет дело с данными, качество которых либо вообще не известно, либо оставляет желать лучшего. Чаще всего не известен и тип распределения случайных переменных.

3. В условиях переходной экономики происходят кардинальные изменения в структурах (спроса, потребностей, цен, технологического базиса и т. д.), причем, оценить, произошло ли, и если произошло, то когда такое структурное изменение, довольно трудно. А следовательно, довольно трудно понять, можно ли доверять результатам математического прогнозирования.

Поэтому в условиях переходной экономики математические методы прогнозирования справедливо занимают гораздо более скромное место, чем в сформировавшейся экономике. В этой ситуации математические методы могут применяться при прогнозировании:

1) краткосрочном, когда вероятность структурных изменений достаточно низка;

2) при условии, что исходные статистические данные соответствуют требованиям, предъявляемым конкретным математическим методом;

3) с верификацией результата другим методом.

С учетом приведенных условий и ограничений можно приступать к математическому прогнозированию, планированию.

Временной ряд при экстраполяции представляется в виде суммы детерминированной (неслучайной) составляющей, называемой трендом, и стохастической (случайной) составляющей. Тренд характеризует существующую динамику развития процесса в целом. Случайная составляющая отражает случайные колебания или шумы процесса.

Условно прогнозная экстраполяция может быть разделена на два этапа. Первым этапом экстраполяции является выбор оптимального вида функции, описывающей эмпирический ретроспективный ряд. Для этого ретроспективный ряд предварительно обрабатывается. Производится преобразование исходных данных с целью облегчения выбора вида тренда. При этом используют сглаживание и выравнивание временного ряда. Кроме этого, в тех же целях могут определять функции дифференциального роста, проводить формальный, в частности, логический анализ процесса или объекта прогнозирования.

На втором этапе экстраполяции производится расчет коэффициентов выбранной экстраполирующей функции. Наиболее распространенными методами оценки коэффициентов являются метод наименьших квадратов и его модификации, метод экспоненциального сглаживания и т. д.

Метод наименьших квадратов. Метод применим, если за время упреждения функции, структура объекта прогнозирования не изменяются, а могут изменяться только значения его параметров. Использование метода наименьших квадратов

предполагает обязательное удовлетворение целого ряда предпосылок. Перечислим эти предпосылки /8/:

1. Случайные ошибки имеют нулевую среднюю (отсутствуют систематические ошибки), конечные дисперсию и ковариацию.

2. Каждое измерение случайной ошибки характеризуется нулевым средним, не зависящим от значений наблюдаемых переменных.

3. Дисперсии каждой случайной ошибки одинаковы, их величины независимы от значений наблюдаемых переменных (гомоскедастичность).

4. Отсутствует автокорреляция ошибок, т. е. значения ошибок различных наблюдений независимы друг от друга.

5. Нормальность, т. е. случайные ошибки, имеют нормальное распределение.

6. Значения тренда (эндогенной, т. е. внутренней переменной) свободны от ошибок измерения и имеют конечные средние значения и дисперсии.

Невыполнение этих предпосылок может сделать применение этого метода некорректным или привести к чрезмерным ошибкам прогноза.

Сущность метода состоит в отыскании коэффициентов модели тренда, приводящих к минимизации ее отклонения от точек исходного временного ряда:

где: - расчетные значения тренда;

-фактическое значение ретроспективного ряда; - число наблюдений.

Если модель тренда представить в виде:

где: а₁,а₂,...,а_k -параметры модели; t - время; Х_i - независимые переменные;

то для того, чтобы найти параметры модели, удовлетворяющие условию минимума S, необходимо приравнять нулю первые производные величины S по каждому из коэффициентов a_i. Решая полученную систему уравнений с к неизвестными, находим значения коэффициентов а-,.

Выбор модели в каждом конкретном случае осуществляется по целому ряду статистических критериев, например, по дисперсии, корреляционному отношению и др. Следует отметить, что названные критерии являются критериями апрокси-мации, а не прогноза. Однако, принимая во внимание принятую

гипотезу об устойчивости процесса в будущем, можно предполагать, что в этих условиях модель, наиболее удачная для апроксимации, будет наилучшей и для прогноза /7/.

В ряде случаев при исследованиях для выбора вида функциональной зависимости используется прием, основанный на том, что определенные соотношения между изменениями входной и выходной величины предполагают ту или иную функциональную зависимость. При соответствующих отношениях входных и выходных величин могут быть рекомендованы следующие апроксимирующие зависимости:

Важной характеристикой прогноза с применением метода наименьших квадратов является оценка точности и достоверности полученного результата.

Наиболее простыми и применимыми практически оценками точности являются: средняя относительная ошибка оценки, среднее линейное отклонение.

Средняя относительная ошибка оценки может быть найдена по формуле:

Среднее линейное отклонение может быть найдено по формуле:

Для оценки точности решения большинства практических задач прогнозирования этого оказывается достаточно. Это связано с относительно невысокой точностью и достоверностью исходных данных. Однако в некоторых случаях, например, фундаментальных исследований, для оценки точности и достоверности результата прогноза используется целый ряд статистических характеристик /8/. В частности, определяют границы доверительного интервала, внутри которого будет лежать прогнозируемое значение зависимых переменных с заданной доверительной вероятностью. При этом считается, что ошибки прогноза распределены нормально относительно линии регрессии и взаимно независимы.

При использовании в процессе математического прогнозирования современных программных продуктов прогнозист (он же пользователь ЭВМ) задает исходные ретроспективные данные, вид апроксимирующей функции. На выходе, в результате работы ЭВМ прогнозист получает как оценку прогнозируемого параметра, так и оценки точности и достоверности этого прогноза.

Классический метод наименьших квадратов предполагает равноценность исходной информации. Однако, на практике, зачастую, будущее поведение объекта или процесса прогнозирования в большей степени определяется поздними наблюдениями, чем ранними. Это обстоятельство породило прием дисконтирования информации. Формальных процедур выбора коэффициента дисконтирования не разработано. Обсуждаемые коэффициенты выбираются исследователем интуитивно, что может снижать точность прогнозирования.

Спектральный анализ /7/. Этот метод позволяет прогнозировать процессы, динамика которых содержит колебательные или гармонические составляющие. К такого рода процессам относятся сезонные колебания спроса, макроэкономические процессы, энергопотребление и т. д.

При описании такого процесса выделяют четыре компоненты прогнозной модели:

x₁(t) - вековой уровень, описывается гладкими апериодическими функциями;

x₂(t) - сезонные колебания с двенадцатимесячным периодом;

x₃(t) - колебания с периодом, большим, чем двенадцать месяцев;

q(t) - случайные колебания с широкими по диапазону периодами, но небольшой интенсивностью.

Модель имеет вид:

x(t) = x₁(t) + x₂(t) + x₃(t) + q(t).

Для расчета первой компоненты модели можно использовать экспоненциальное сглаживание.

где: 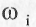- частота колебаний; b_i, c_i - амплитуды колебаний; - ошибка.

Методическая основа метода - анализ периодограмм.

Факторный анализ /7/ позволяет проводить максимально возможный учет совокупности переменных, характеризующих объект, и взаимосвязи между ними. При этом прогнозист вынужден искать компромисс между числом переменных в описании, отражающем полноту прогноза, и его сложностью, трудоемкостью. Факторный анализ представляет собой раздел математической статистики и включает большое число методов.

Поиск по сайту: