Проектирование объектов испытаний

При исследовании испытаний должны учитываться функции, организационная структура, особенности власти и другие факторы объекта испытаний, способные повлиять на результат.

Для проектирования испытаний систем управления прежде всего необходимо спроектировать или выделить объект испытаний. При проведении управленческих экспериментов в ОПС объект испытаний может совпадать или составлять часть ОПС.

Проектирование процесса испытаний также следует начинать с синтеза объекта или некоторого множества (номенклатуры) объектов испытаний. Это связано со следующим. В процессе испытаний подвергающиеся этим испытаниям объекты (системы управления, товары) могут разрушаться (например, при испытаниях на прочность), дорабатываться с целью улучшения их свойств, вырабатывают ресурс, утрачивают товарный вид и т.д.

Если в качестве объекта на всех этапах испытаний использовать только объект (систему управления, товар) в рыночной (штатной) комплектации, то это может приводить:

1) к «затягиванию» выхода на испытания - выходу на них только после разработки и испытаний всех комплектующих и подсистем (Это увеличит срок разработки системы управления, товара с соответствующим замедлением оборота денежных средств, ухудшением конкурентной позиции фирмы-производителя.);

2) к утрате образца полностью даже в том случае, когда в конкретном эксперименте не используются некоторые его функции и свойства (Это приведет к нерациональному расходу средств на производство опытных образцов. Поэтому на практике часто проектируют некоторый ряд - номенклатуру объектов испытаний. Эта номенклатура объектов испытаний должна быть рациональной, то есть позволять решать задачи испытаний. Если такая номенклатура еще и обладает определенным свойством, например, минимума стоимости, то представляется возможным говорить об оптимальной номенклатуре объектов испытаний.).

Провести проверку полноты реализации функций испытуемой системы при проведении испытаний с использованием синтезированной номенклатуры объектов испытаний

можно сравнением таблиц функций цели, адаптации, живучести исходной системы и соответствующих суммарных (полученных посредством логического сложения) таблиц для синтезированной номенклатуры объектов испытаний.

Проверку степени возможной избыточности множества функций, реализация которых возможна с использованием синтезированной номенклатуры объектов испытаний, можно выполнить, установив, сколько раз при использовании этой номенклатуры реализуется каждая из функций исходного объекта испытаний. Если в результате такой проверки будет установлено, что какая-либо из функций реализуется более двух раз, то существует вероятность того, что номенклатура объектов испытаний избыточна, то есть имеет место превышение множества функций синтезированной номенклатуры объектов испытаний над соответствующим множествам функций исходного товара. В этом случае необходимо провести дополнительные исследования. Если будет установлена излишняя избыточность, то она может быть устранена. Более подробно эта проблема рассматривается в работе/2/.

Лишь после проектирования номенклатуры объектов испытаний разрабатывают планы испытаний.

4.4. Методы теории планирования экспериментов

Наиболее часто на практике встречаются недостатки испытаний систем управления, связанные с тем, что в процессе испытаний:

1) проверяют не все, а только часть функций (не обеспечивают функциональную полноту испытаний), что снижает техническую достоверность результатов испытаний;

2) выбранные условия испытаний (план испытаний) не позволяют достичь наихудших (максимальных или минимальных) значений воздействующих факторов, что тоже не позволяет обеспечить достоверность результата испытаний;

3) длительность одного эксперимента и число экспериментов недостаточны для того, чтобы случайный отказ проявился;

4) малое число экспериментов не позволяет с достаточными статистическими точностью и достоверностью оценить параметры товара (Это повышает неопределенность при принятии решения о соответствии товара предъявляемым требованиям и, соответственно, возможности его реализации потребителям.);

5) в процессе анализа неправильно интерпретируют результаты экспериментов и это приводит к неправильной диагностике причин и последствий наблюдавшихся в процессе испытаний отклонений параметров, отказов.

Классификация методов планирования экспериментов может быть связана с используемыми при планировании моделями объектов экспериментальных исследований.

Различия в моделях вызывают две трактовки состава множества методов математической теории планирования эксперимента:

1) в соответствии с первой (узкой) трактовкой эту теорию отождествляют с регрессионным и факторным планированием (При разработке таких планов рассматривают и используют регрессионные модели объектов испытаний. Однако большинство реальных объектов не может быть описано регрессионными моделями, в том числе, в силу дискретности реальных процессов, исследуемых в системе управления.);

2) в соответствии со второй (расширенной) трактовкой под математической теорией планирования эксперимента понимают совокупность математических методов, каждый из которых позволяет в соответствии с определенными задачами испытаний найти необходимые условия или(и) количество реализаций эксперимента/4/. При этом рассматриваются имитационные модели (функциональные испытания), и частные виды моделей: модели повышения обученности, модели надежности объектов испытаний и другие.

При широком подходе к методам теории планирования экспериментов могут быть отнесены/5/:

• логико-математические функциональные планы: полный,интегральный, усеченный/4,5/;

• регрессионное, факторное планирование/3,6/;

• интерпретация испытаний как процесса повышения «обученности» системы/7/;

• интерпретация испытаний как процесса повышения надежности/8/;

• статистический корреляционный метод/9/;

• расчет на основе базовых коэффициентов/9/;

• методы переводных коэффициентов и бальных оценок, рассматриваемые как разновидности метода базовых коэффициентов, а также модификация этого метода, используемая иногда с целью повышения точности метода/9/;

• расчет объемов испытаний (числа экспериментов) для обеспечения статистической достоверности (доверительной вероятности) результата испытаний/10/;

• использование условных вероятностей (теоремы Байеса) для оценки условной вероятности достижения результата в зависимости от уровня затрат на это /11/;

• использование функций штрафа для определения объемов испытаний, обеспечивающих минимум суммарных затрат на испытания и устранение недостатков в процессе эксплуатации/12/.

В связи с тем, что достаточно полное изложение только одного из перечисленных методов потребует отдельной книги и может увести нас от основной темы книги настоящей, лишь кратко охарактеризуем наиболее практически значимые методы.

Это будет сделано с таким расчетом, чтобы исследователь:

• во-первых, понял необходимость и пользу применения этих методов в реальной деятельности при прогнозировании и планировании испытаний;

• во-вторых, мог оценить возможность и целесообразность использования конкретного метода в условиях практической задачи;

• смог найти более полное описание соответствующего метода с использованием рекомендованной литературы.

При этом основы функционально-логического и регрессионного планирования испытаний изложены в отдельных нижеследующих параграфах этой главы.

В параграфе 4.8 рассмотрено использование типовых представлений для выбора метода планирования испытаний/5/.

В настоящем параграфе рассмотрены некоторые из перечисленных методов планирования экспериментов.

В работе/8/ дают методику построения плана при интерпретации испытаний как процесса повышения надежности. Эффективность экспериментальной отработки (испытаний) жидкостного ракетного двигателя характеризуют достигнутым уровнем надежности, а также затратами средств и времени на отработку. Представляется, что эта методика применима для испытаний сложных технических систем произвольного назначения, включая автоматизированные системы прогнозирования и планирования. Это связано с тем, что, по сути, летные испытания являются испытаниями товара в натурных, т. е. естественных, условиях эксплуатации.

Критерий оптимизации экспериментальной отработки формулируют как достижение заданного уровня надежности при минимальных затратах средств или времени.

В названной работе конкретизируют задачи этапа летных испытаний жидкостного ракетного двигателя, анализируют оптимальное распределение ресурсов между этапами стендовой (лабораторной) отработки и летных испытаний.

Оптимизацию производят, исходя из условия подтверждения надежности, сформулированного в виде:

Р=1, Р_н>Р_нз при j>j₃,

где: Р - частотность безотказной работы;

Р_н, Р_Нз - соответственно, расчетное и заданное значение нижней границы одностороннего доверительного интервала вероятностей безотказной работы.

j, j₃ - соответственно, принятое для расчета и заданное значение доверительной вероятности.

Этапы стендовых доводочных испытаний и летных испытаний рассматривают как последовательности испытаний жидкостного ракетного двигателя штатной конструкции, квалифицированных как успешные.

Представляют доверительную вероятность j₃ в виде:

где: j_им - доверительная вероятность, связанная с полнотой и достоверностью имитации летных условий;

j_n - доверительная вероятность, обусловленная ограниченностью объема выборки.

Используя отношение:

получают следующие зависимости для определения потребных объемов безотказных стендовых N_си и летных испытаний N_ли для подтверждения Р_нз:

т.к. в последнем случае: j_им=1. Очевидно, что N_СИ>N_ЛИ.

Допускают, что увеличением объема стендовых испытаний можно компенсировать определенную неуверенность в достоверности имитации летных условий, если при этом j_им > j₃. Из приведенных выше соотношений можно найти эквивалент летных и стендовых испытаний:

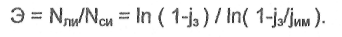
Следовательно, если проведено N_си стендовых и Н_лилетных испытаний, то эквивалентное, т. е. приведенное к летным условиям число испытаний, запишется в виде:

Считают, что, если капиталовложения на имитацию летных условий находятся в области допустимых значений, то наибольший экономический эффект достигается только результатами стендовых испытаний. Однако этот вывод не может быть признан достаточно корректным, так как практически невозможно в наземных условия создать комплекс летных условий, а связанная с этим неопределенность может быть источником отказов в реальном полете (эксплуатации).

В работе /7/ дается математическая модель многоступенчатого процесса испытаний, рассматриваются критерии эффективности процесса испытаний, исходя из представления экспериментальной отработки как процесса повышения «обученности» объекта испытаний. Испытания рассматривают в качестве своеобразной обратной связи, направленной на уточнение параметров проектируемой системы. В результате воздействия этой связи оценивают соответствие проектируемой системы предъявляемым к ней требованиям, т.е. оценивают ее текущую эффективность, выявляют причины возможного

несоответствия и вырабатывают управляющие воздействия, направленные на устранение этого несоответствия. Указывается, что, исходя из такой интерпретации, в качестве технического критерия - эффективности испытаний - можно применить рассогласование Q(t) между заданным Wз и текущим W(t) значениями эффективности товара:

Q (t) = W₃ - W (t).

Отмечают, что такой критерий не учитывает затрат, необходимых для достижения требуемого значения эффективности, причем, под затратами можно понимать как время, так и стоимость испытаний. Такие затраты учитывает критерий вида:

Э(t) =W(t)/S(t),

где: Э (t) - обобщенный критерий эффективности;

W (t) - выходной эффект системы;

S (t) - затраты на достижение выходного эффекта.

Для определения количественных оценок эффективности в соответствии с приведенным критерием необходимо получить зависимости, связывающие текущую эффективность со временем и стоимостью испытаний.

Степень повышения эффективности системы в процессе ее экспериментальной отработки может быть различной и зависит как от специфики проектируемой системы, так и от конкретного содержания испытательных программ, принятой методики, совершенства испытательного оборудования.

Для получения зависимости текущей эффективности от времени испытаний необходимо располагать математической моделью процесса испытаний. Для построения такой модели авторы рассматривают основные свойства процесса обнаружения дефектов.

Предполагается, что комплексная программа испытаний имеет иерархическую структуру. Каждое частное испытание проводится по единой программе с неизменными условиями и носит название единичного испытания.

Для построения математической модели предполагают, что все дефекты одинаковы с точки зрения возможности их обнаружения. Авторы отмечают, что это не так, потому что вероятность перехода дефекта в отказ и, следовательно, вероятность обнаружения дефекта зависит от условий испытаний. Предполагается также, что дефекты независимы, т.е. вероятность обнаружения дефекта не зависит от числа и вида других дефектов, имеющихся в системе, однако в ряде случаев один дефект маскирует другой.

Рост эффективности объекта в процессе испытаний описывают логистической кривой.

где: 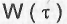- параметр эффективности объекта испытаний;

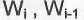- верхнее и нижнее значения диапазона изменения параметра эффективности объекта испытаний на i-том этапе испытаний;

a, b - параметры модели, вычисляемые с использованием метода наименьших квадратов;

е - основание натурального логарифма, равное 2,718; - длительность отрезка времени испытаний.

Если проводится несколько конечных реализаций эксперимента, то:

где: - длительность одной реализаций эксперимента;

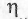- число реализаций эксперимента в программе испытаний.

Одной из важнейших задач планирования испытаний с использованием этого метода является назначение момента перехода от одного этапа испытаний к другому таким образом, чтобы минимизировать суммарные затраты времени и(или) средств на испытания. Это может быть сделано посредством априорного (по результатам моделирования) назначения величин W_i, W_i-1 и допусков на достижение значений W_i в процессе испытаний.

Статистический корреляционный метод, расчет на основе базовых коэффициентов, метод переводных коэффициентов /9/. Они могут рассматриваться как методы прогнозирования и планирования по аналогии. Для их применения необходимо существование достаточно близких аналогов прогнозируемого процесса или объекта.

При использовании статистического корреляционного метода затраты времени и(или) средств можно определить с использованием специальных формул.

Расчет на основе базовых коэффициентов /9/ выполняют на основе учета затрат по различным видам работ.

Метод переводных коэффициентов /9/ является разновидностью расчета на основе базовых коэффициентов.

Описание этих методов с формулами приведено в п. 5.4.

Математическая статистика /10/ позволяет дать прогноз числа экспериментов, обеспечивающих заданные точность и достоверность результата прогнозирования. Для этого необходимо задать величину доверительного интервала, доверительную вероятность и, используя методы математической статистики, вычислить необходимое число экспериментов.

Метод условных вероятностей /11/ позволяет получить оценку вероятности выполнения работы, достижения заданного состояния (уровня эффективности) объекта прогнозирования при различных уровнях затрат, используя теорему Байе-са. Пример реализации такого планирования при строительстве дан в работе /11/.

Метод штрафных функций /12/. В соответствии с этим методом объем испытаний назначается исходя из информации о стоимости затрат на устранение выявленных недостатков на этапе испытаний и при эксплуатации, с учетом интенсивностей отказов, порождаемых различными источниками.

Основным недостатком этих методов является то, что в рамках этих методов рассматривается только вопрос оценки объема (числа реализаций, суммарного времени) испытаний, а следовательно, затрат на такие испытания. При этом важнейший для принятия решения о передаче системы управления, товара в эксплуатацию вопрос о назначении условий испытаний оказывается вне рамок этих методов.

Решение о применении того или иного метода планирования эксперимента определяется объемом располагаемой об объекте испытаний информации (видом его типового представления)/5/.

4.5. Регрессионное и факторное планирование экспериментов

Регрессионное и факторное планирование экспериментов подразумевает возможность построения аналитической регрессионной модели объекта испытаний/3, 6/. Такое планирование наиболее часто используется при исследованиях систем управления технологическими процессами.

Регрессионные планы испытаний позволяют как определить условия испытаний, так и оценить необходимое число экспериментов для достижения целей испытаний. Таким образом определяют затраты на проведение испытаний.

Предполагается три степени информированности исследователя относительно модели объекта испытаний:

1) модель (функция) 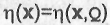известна. Требуется оп-

ределить или уточнить неизвестные параметры модели:

2) известно, что функция совпадает с одной из

функций:

Требуется определить, какая из функций , ,

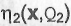..., является истинной, и найти неизвестные параметры модели.

3) вид функции не известен. Известно лишь, что эта

функция в интересующей исследователя области может быть достаточно хорошо апроксимирована конечным рядом по некоторой системе заранее заданных функций. Требуется найти наилучшее описание функции

Факторным пространством называют пространство размерности п, в котором определен вектор X, значения которого в i-том эксперименте равны значениям контролируемых переменных, занумерованных в удобном для экспериментатора порядке.

Задачи факторного планирования возникли при сельскохозяйственных исследованиях, но потом стали использоваться в других областях деятельности /6/. Как и регрессионные планы, планы факторные относятся к методам математической статистики. Важное отличие от регрессионного планирования состоит в том, что рассматривается фиксированное число уровней контролируемой переменной. При факторном планировании рассматривают количественные и качественные переменные.

Количественной называют переменную, все значения которой рассматриваются как некоторые числа.

Переменную называют качественной переменной, если хотя бы одно ее значение рассматривается как символ (может быть записанный в виде числа).

Строгий способ введения этих понятий заключается в следующем: считать качественными переменными те, для которых рассматривается модель для качественных переменных, и считать количественными переменными те, для которых рассматривается модель для количественных переменных.

При факторном планировании каждое из различных значений, которые принимает переменная X_i в плане D_xi={X_iU},(i=1,..., m; u=1,.... N) называют уровнем. Число различныхуровней одной переменной X_i обозначают через S_i. Каждомуиз различных уровней переменной X_i ставят в соответствиесимволы 0,1........................................................................... S_i-1, независимо от того, является ли переменная Х_i количественной или качественной. В этом случае говорят о факторе F_i, принимающем значения 0,1,..., S_i-1. Тогда

матрица плана может быть переписана в следующем виде:

План называют симметричным, если все факторы имеют одинаковое число уровней.

План называют равномерным, если уровни любого фактора встречаются вплане одинаковое для данного фактора число раз.

План называют факторным в случае определенного типа модели, для которой данный план рассматривается. Типы моделей ипримеры приведены в работе/6/.

План, содержащий N = S_i*...* S_m различных опытов, называют полным факторным планом.

План, содержащий меньшее число опытов, называют дробным планом.

Для оценки значений зависимой переменной (параметров эффекта) используют регрессионные модели и метод наименьших квадратов, описанный в третьей главе.

Часто под факторным планом понимают множество точек факторного пространства с относительными значениями параметров -1 и +1 (то есть рассматриваются всего два уровня факторов: максимальный и минимальный). Такой факторный план включает комбинации из наибольших и наименьших значений каждого из факторов. Он содержит 2^m экспериментов (где m - число факторов). Иногда в факторные планы включают центральную точку плана, соответствующую средним абсолютным значениям факторов, то есть рассматривают три уровня факторов.

Факторное планирование эксперимента может быть априорным статистическим и непрерывным (последовательным).

Под статистическим (в рамках регрессионного) планированием эксперимента здесь понимается априорное планирование всего множества экспериментов в целом до их начала. Для широкого класса функций статистическое планирование экс-

периментов заключается, по существу, в использовании готовых таблиц, описывающих характеристики оптимальных планов /3/.

Под последовательным планированием понимают планирование экспериментов по этапам с учетом полученных на предыдущих этапах результатов, вплоть до достижения целей экспериментов.

При последовательном планировании выделенные ресурсы (материальные, время) разбивают на несколько частей, каждая из которых используется для обеспечения соответствующих этапов испытаний. Логическая последовательность действий при последовательном планировании экспериментов включает: «планирование» - «эксперимент» - «анализ» - «планирование». При этом этап «анализ» подразумевает не только обычный регрессионный анализ экспериментальных данных, но и анализ сведений, поступающих извне/3/. Реализация последовательности этапов прекращается при достижении целей экспериментального исследования, в том числе и определения параметров исследуемого процесса с заданной точностью.

С вычислительной точки зрения, последовательное планирование при критерии минимума определителя дисперсионной матрицы, заключается в поиске на каждом этапе минимального значения определителя матрицы/3/:

где: D_u - матрица, состоящая из элементов 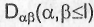, соответ-

ствующих параметрам, интересующим экспериментатора.

План Е₁(Т) будет предпочтительнее плана Е₂(Т), если для одних и тех же затрат первый определитель будет меньше второго:

где: Т - затраты, отведенные на данный эксперимент.

Когда требуется определить, какая из функций , ,..., является истинной, могут проводиться дис-

криминирующие эксперименты /6/.

Планирование дискриминирующих экспериментов заключается в поиске таких точек, результаты измерений в которых позволили бы отличить одну модель от другой и сделать вывод об истинности одной из моделей. При этом может выдвигаться и проверяться совокупность конкурирующих гипотез. В этом случае экспериментатор должен /3/:

1) выдвинуть совокупность конкурирующих гипотез;

2) построить функцию потерь;

3) провести анализ априорных сведений для определениявероятностей появления соответствующих гипотез;

4) выбрать оптимальное решающее правило;

5) оптимально разместить затраты в области планирования эксперимента.

Главными недостатками факторного планирования испытаний многофункциональных систем являются:

1) применение их в том случае, когда возможно описание процесса регрессионной математической моделью (ограничения, накладываемые на вид функции параметров эффекта в зависимости от параметров факторного пространства);

2) большое число необходимых для его реализации экспериментов (при факторном планировании на двух уровнях оно равно 2ⁿ, где п - число факторов, влияющих на исследуемый процесс);

3) отсутствие обоснованных процедур сокращения числа экспериментов в плане в том случае, когда полный факторный план не может быть реализован ввиду отсутствия необходимых опытных образцов, средств или времени на проведение испытаний.

4) технические условия проведения испытаний не рассматриваются, что порождает риск неадекватности условий;

5) при изменении структуры объекта или условий его функционирования использование любых ранее полученных результатов становятся некорректным.

4.6. Функциональные планы испытаний

Регрессионные, факторные планы строят для ограниченных классов объектов и(или) процессов, которые могут быть описаны аналитическими (регрессионными) математическими моделями. Однако они не пригодны для планирования экспериментов, объектов и процессов, которые не могут быть описаны аналитическими математическими моделями, в частности, регрессионными. А это - большинство реальных объектов. В условиях реальной переходной экономики число дискретных объектов возрастает/1/.

Логико-имитационный метод разработки планов функциональных испытаний разработан для решения практических задач планирования натурных испытаний сложных технических систем/4/. Однако он применим и для планирования испытаний других типов сложных систем управления, товаров.

Функциональные планы строят для объектов, систем управления, имеющих имитационные модели/1,4/. С использованием логико-математических процедур находят условия проведения испытаний функций сложных объектов. При этом обеспечивают достижение наихудших (максимальных или минимальных (экстремальных) факторов, влияющих на работоспособность или(и) эффективность работы объекта испытаний. Условимся считать, что если товар оказался работоспособен в наихудших условиях, то он будет работоспособен и в менее напряженных условиях эксплуатации. Поэтому функциональные планы представляется возможным отнести к экстремальным планам. При таком планировании обеспечивается достоверность результата испытаний и снижается неопределенность при принятии решения о возможности реальной эксплуатации товара, объекта. Процедуры проверки адекватности и верификации моделей выполняются отдельно и до начала планирования.

На практике нередки ситуации, когда полный функциональный план не может быть реализован ввиду отсутствия необходимых опытных образцов, средств или времени на проведение испытаний. Различают полные, интегральные, усеченные функциональные планы/4/. То, какой из этих планов может быть построен, определяется соотношением необходимого для реализации соответствующего плана числа экспериментов и реально располагаемым числом экспериментов.

Функциональный план испытаний строится в несколько этапов. Вначале с использованием имитационной модели исследуют реализацию тех или иных функций цели. Затем анализируют данные, полученные при моделировании различных

функций. Сравнивают необходимое для реализации плана данного вида число экспериментов и то число экспериментов, которое может выполнить исследователь. По результатам этого анализа, собственно, и принимают решение о том, какой из типов планов функциональных испытаний: полный, интегральный, усеченный, строить. Реально располагаемое число экспериментов может ограничиваться числом изготовленных опытных образцов, объемом выделенных на проведение испытаний средств; ограничениями на время, проведения испытаний, накладываемыми конкурентной борьбой и другими соображениями.

Переход от полного к интегральному, от интегрального к усеченному функциональному планам сопровождается дозированным и осознанным снижением объема информации об объекте испытаний. Это плата за снижение стоимости и(или) продолжительности испытаний.

Цель построения полных функциональных планов -проверить правильность функционирования и работоспособность объекта испытаний во всех заданных режимах.

Построить полный функциональный план значит найти минимальное множество условий эксперимента, обеспечивающих проверку связности графа структуры объекта испытаний при экстремальных значениях каждого из внешних факторов при реализации каждой функции.

Для нахождения элементов полного функционального плана используют следующую процедуру:

1) разрабатывают функционально-декомпозиционное представление объекта испытаний, прогнозирования, планирования;

2) статистическим или комбинированным детерминирован-но-статистическим (часть условий назначается испытателем-прогнозистом, а другая выбирается случайно) моделированием определяют возможные пути (траектории) достижения желаемого конечного состояния;

3) рассчитывают соответствующие этим путям расход ресурсов и другие параметры как функцию времени;

4) определяют экстремальные значения каждого из этих параметров в процессе опытной реализации одной функции;

5) запоминают номер функции и подмножество начальных условий, при которых достигаются экстремальные значения каждого из факторов, а также соответствующие максимальные значения факторов;

6) реализуют п.п.2-5 для каждой функции ОПС;

7) определяют множество условий эксперимента (элементов плана) однократным перечислением подмножеств условийдля реализации одного эксперимента, при которых достигаютсямаксимальные значения каждого из факторов при реализациикаждой из функций.

Полученный таким образом план обладает свойствами внешней и внутренней устойчивости. Число элементов полного

функционального плана (Nⁿ) может достигать значения, равного произведению числа функций на число факторов:

 

где: G - число функций цели объекта испытаний; - число факторов.

Если же реальные ограничения не позволяют реализовать такое число экспериментов, то строят интегральный или усеченный функциональные планы.

Рассмотрим методику построения этих планов на гипотетическом примере.

Пример. Пусть объект испытаний реализует две функции цели: F₁^T, F₂^t. При этом число факторов - параметров, влияющих на его функционирование, равно трем: х ₁, х ₂, х ₃.

Пусть при реализации первой функции цели с использованием имитационной модели наблюдались следующие последовательности значений параметров:

1) в первом имитационном эксперименте (условия Y₁) имели место значения факторов, приведенные в таблице 4.1.

Таблица 4.1.

 

Факторы	Время имитационного эксперимента
t1	t2	t3	t4	t5	t6
х1
х2
х3

2) во втором имитационном эксперименте (условия Y₂) имели место значения факторов, приведенные в таблице 4.2.

Таблица 4.2.

 

Факторы	Время имитационного эксперимента
t1	t2	t3	t4	t5	t6
х1
х2
х3

3) в третьем имитационном эксперименте (условия Y₃) имели место значения факторов, приведенные в таблице 4.3.

Таблица 4.3.

 

Факторы	Время имитационного эксперимента
t1	t2	t3	t4	t5	t6
х1
х2
х3

4) в четвертом имитационном эксперименте (условия Y₄) имели место значения факторов, приведенные в таблице 4.4.

Таблица 4.4.

 

Факторы	Время имитационного эксперимента
t1	t2	t3	t4	t5	t6
Xi
х2
х3

На первом шаге построения полного функционального плана находят максимумы каждого из параметров по времени реализации каждого эксперимента. При этом получают следующие последовательности значений:

х₁₁^t ={6,5,8,4}

x₂₁^t={7,4,4,3}

Х₃₁^t ={4, 5, 4, 3}.

На втором шаге построения полного функционального плана находят максимумы параметров по номеру реализации эксперимента. Эти значения выделены жирным шрифтом. Это:

Х₁₁³=8, х₂₁¹=7, х₃₁²=5.

В план испытаний Y функции F₁^T включают условия проведения испытаний Y={Y₃¹, Y¹¹, Y²¹}, обеспечивающие максимальное значение:

• параметра х₁ в комплексе начальных условий эксперимента под номером три (Y₃¹),

• параметра х₂ в комплексе начальных условий эксперимента под номером один (Yi¹),

• параметра х₃ в комплексе начальных условий эксперимента под номером два (Y₂¹).

Комплекс начальных условий эксперимента под четвертым номером в план испытаний функции F₁^T не включают, так как при этих условиях ни один из параметров не достигает максимального при реализации этой функции значения. Следовательно, эксперимент в комплексе условий Y₄ не позволит подтвердить работоспособность объекта испытаний и является малоинформативным. Проведение эксперимента в этих условиях приводит к менее эффективному расходованию средств на испытания. Если же эксперимент будет проведен в этих условиях вместо выбранных выше, то возрастает риск принятия в эксплуатацию товара, который может оказаться неработоспособным в возможных «более тяжелых условиях эксплуатации».

При построении полного функционального плана по аналогии с приведенным выше выбором условий для испытаний функции F₁^T определяют условия испытаний и для других

функций. Эти условия в их совокупности и составляют полный функциональный план. Для реализации такого плана для двух функций необходимо провести 2*3=6 экспериментов.

Однако может оказаться, что реально располагаемое число экспериментов меньше. Тогда строят интегральный функциональный план.

Предположим, что в результате имитационного моделирования и выполнения действий, аналогичных выполненным по отношению к функции F/, для функции F₂ найдены:

х₁₂^t={3,2,5, 1},

х₂₂^t={4,3,2,2},

х₃₂^t={6,2,3,3},

х₁₂³=5, х₂₂¹=4, х₃₂¹ =6.

Сравнивая эти значения с ранее полученными Х₁₁³ =8, Х₂₁¹=7, х₃₁²=5, нетрудно установить, что только в одном комплексе условий, а именно, х₃₂¹ =6 при реализации функции F₂ достигаются большие значения фактора, чем при реализации предыдущей функции.

В интегральный план испытаний Y_и функций F₁^T₂ и F₂^T включают условия проведения испытаний Y_и = {Y₃¹,Y₁¹,Y₁²}, которые обеспечивают:

1) проверку работоспособности функций F₁^T и F₂^T;

2) испытания на проверку работоспособности в максимально тяжелых условиях при реализации как функций F₁^T,так и F₂^T.

Число экспериментов в таком интегральном функциональном плане равно трем.

Если бы оказалось, что во всех случаях максимальные значения параметры принимают при реализации только первой функций F₁^T, то это свидетельствовало бы, что реализация второй функции не сопровождается максимальными воздействиями. В этом случае исследователю было бы достаточно только проверить работоспособность при реализации функции F₂^T в любом из комплексов условий F₁² или F₃².

В этом случае интегральный функциональный план для испытания функций F₁^T и F₂^T мог бы иметь вид:

Как мы видим, число экспериментов в интегральном функциональном плане в этом случае было бы равно 4.

Интегральный функциональный план позволяет произвести проверку всех функций (связности графа структуры) при максимально возможных на всем множестве условий эксплуатации значениях факторов.

Построить интегральный функциональный план можно в результате выполнения следующих действий:

1) проводят 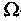-разбиение полного функционального плана на подмножества элементов, обеспечивающих максимальные значения по каждому из факторов ( -число факторов);

2) на каждом из подмножеств находят элемент, максимальный среди максимальных, вошедших в полный функциональный план;

3) запоминают соответствующие номер функции, комплекс начальных условий, номер фактора;

4) выполняют п.п. 2, 3 для всех подмножеств -разбиения;

5) проверяют, все ли функции объекта испытаний представлены в числе запомненных в п.З комплексов условий эксперимента;

6) если все функции вошли в подмножество, полученное в результате реализации п.п. 2-4, то это подмножество и есть интегральный функциональный план, и процедура его построения завершается;

7) если не все функции объекта испытаний вошли в подмножество, полученное в результате реализации п.п.2-4, то это подмножество дополняют элементами полного функционального плана, еще не представленными в интегральном функциональном плане, до тех пор, пока все функции не будут один раз представлены в интегральном функциональном плане.

Максимальное число элементов в интегральном функциональном плане может быть найдено по формуле:

где: G - число функций цели объекта испытаний; 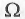- число факторов. Минимальное число элементов в интегральном функциональном плане может быть найдено по формуле:

Но может оказаться, что у исследователя нет возможности реализовать и интегральный функциональный план. Тогда, исходя из располагаемого числа функциональных экспериментов, строят усеченный функциональный план.

Усеченные функциональные планы позволяют построить план испытаний многофункционального объекта с любым числом экспериментов посредством «усечения» (то есть исключения после анализа значимости данного эксперимента) функций или внешних факторов.

При построении усеченного функционального плана стремятся извлечь максимум информации о связности графа структуры (реализуемости функций) и проверить работоспособность при максимально возможных или наихудших, наилучших значениях факторов. При этом важно определить понятие «информативность», применительно к решаемой задаче. Кроме того, важно установить отношения предпочтительности испытаний

одной функции или достижения максимума по одному из факторов по отношению к другим.

Функции могут быть ранжированы по частоте реализации. Факторы могут быть ранжированы с использованием статистических данных или экспертных методов по их тяжести для конкретного типа объектов испытаний и условий эксплуатации.

При другом подходе функции могут быть ранжированы по сложности, например, в соответствии с числом подсистем, участвующих в их реализации. При этом функции присваивают высший ранг, если в ее реализации участвует большее число подсистем.

Усечение функций и(или) факторов проводится до тех пор, пока располагаемого числа экспериментов становится достаточно для реализации интегрального функционального плана для объекта испытаний с усеченными функциями и(или) факторами.

Такая процедура позволяет дозировано, после предварительного анализа и оценки значимости той или иной информации, которую предполагается получить в ходе экспериментов, проводить сокращение числа экспериментов в ходе построения последовательности: «полные - интегральные - усеченные» функциональные планы/4/.

1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 |

Поиск по сайту:

---