Лекции 3-4. Основные положения квантово-механической теории строения атома

Квантово-механическая теория строения вещества является фундаментальной научной концепцией современного естествознания, открывающей принципиально новые подходы к изучению мира микрочастиц (элементарных частиц, атомов, молекул и надмолекулярных структур), закономерности которого не могут быть выведены из законов макромира, описываемого классической физикой. Квантовая механика в своей основе сформировалась в 1924-27 годах, однако некоторые предпосылки, послужившие отправной точкой для этой теории, относятся к началу XX века.

Первой предпосылкой возникновения квантово-механической теории следует считать квантовую теорию электромагнитного излучения. В 1900 г М. Планк, изучая спектр абсолютно черного тела, сформулировал основное положение этой теории следующим образом:

- лучистая энергия испускается и поглощается дискретно в виде целого числа квантов энергии;

- энергия кванта определяется частотой излучения и может быть рассчитана по уравнению Планка

E = hn

где h - постоянная Планка (6,625×10^-34 Дж×с), n - частота излучения.

Следующей предпосылкой рассматриваемой теории явилось объяснение закономерностей фотоэффекта - испускания электронов при облучении поверхности металла светом. Экспериментально было установлено, что кинетическая энергия фотоэлектронов зависит от частоты излучения, но не зависит от его интенсивности. От интенсивности излучения зависит только число электронов, т.е. сила фототока, хотя в рамках классической электромагнитной теории света энергия фотоэлектронов должна меняться с изменением интенсивности падающего света и не должна зависеть от частоты излучения. А. Эйнштейн (1905 г.) показал, что это противоречие можно устранить, если принять, что свет имеет двойственную природу, являясь одновременно пакетом электромагнитных волн, энергия которых описывается уравнением Планка, и потоком фотонов - частиц с нулевой массой покоя. В этом случае кинетическая энергия фотоэлектрона будет определяться следующим соотношением:

Е_к = Е_ф – А

где Е_ф - энергия фотона, А - работа, которую необходимо затратить на удаление электрона из металла (работа выхода).

С учетом уравнения Планка

Е_к = hn - А

то есть энергия фотоэлектронов зависит от частоты излучения и не зависит от его интенсивности.

Третьей предпосылкой квантовой механики является ядерная (планетарная) модель атома, предложенная Э. Резерфордом (1911 г.), в соответствии с которой атом представляет систему из положительно заряженного ядра и связанных с ним электронов. Хотя от "планетарного" характера движения электронов вокруг ядра позже пришлось отказаться, ядерная модель атома остается общепризнанной.

В 1913 г. Н. Бор показал, что устойчивость атома водорода и происхождение линий в его спектре могут быть объяснены, если допустить, что разрешенные значения энергии электрона меняются дискретно, а энергетическим уровням отвечают стационарные орбиты определенного радиуса, пребывая на которых электрон не поглощает и не излучает энергию. Теория Бора позволила с высочайшей степенью точности рассчитать атомный спектр водорода, однако распространить ее на другие атомы не удалось. Таким образом к началу двадцатых годов XX века необходимость в новом подходе к описанию объектов микромира стала очевидной.

В основе квантово-механической теории строения атома лежит планетарная модель Э. Резерфорда, согласно которой атом состоит из положительно заряженного ядра и вращающихся вокруг него электронов (электронной оболочки).Основные положения современной квантово-механической теории строения электронной оболочки атома были заложены в 1924 - 1927 годах группой выдающихся физиков-теоретиков: Н. Бор, Луи де Бройль, Э. Шредингер, В. Гейзенберг, М. Планк и др. В основе данной теории лежат два постулата:

1. Принцип неопределенности (В. Гейзенберг, 1927 г.) - невозможно одновременно с высокой точностью определить положение электрона в пространстве (координаты) и его импульс (p = mu).

Продемонстрируем справедливость этого принципа с помощью следующего мысленного эксперимента. Пусть движущийся электрон освещают потоком фотонов, а отраженные фотоны регистрируют с помощью некого идеального детектора, пытаясь таким образом установить координаты и импульс микрочастицы. Положение частицы в пространстве задается координатами x, y, z, а ее импульс, являющийся векторной величиной, - его проекциями на координатные оси (p_x, p_y, p_z). Очевидно, что при этом значение импульса будет характеризоваться некоторой неопределенностью (погрешностью определения), так как при столкновении фотона, имеющего собственный импульс, с электроном импульс последнего изменится. Точно также измерение координат будет проведено с некоторой неопределенностью, связанной с дифракцией фотонов на электроне, вследствие чего образ электрона будет размытым. При этом дифракция будет увеличиваться с увеличением длины волны излучения. Предположим, что наблюдатель желает максимально сократить неопределенность положения электрона, уменьшая для этого длину волны фотона. Однако это влечет за собой увеличение частоты излучения (n = с/l), а также энергии и импульса фотона, так как

p =

где Е_к - кинетическая энергия фотона. В результате в силу закона сохранения импульса столкновение с фотоном существенно изменит импульс электрона, погрешность его определения возрастет, а наблюдаемая траектория электрона станет зигзагообразной.

С другой стороны, уменьшение неопределенности импульса требует уменьшения импульса фотона, для чего необходимо уменьшить его энергию, а, следовательно, увеличить длину волны. Результатом этого будет усиление дифракции, а соответственно, увеличение неопределенности в значениях координат - экспериментатор увидит вместо точки размытое пятно, и не сможет установить, где именно в пределах этого пятна будет находится электрон.

Рассмотренный мысленный эксперимент показывает, что одновременно уменьшить неопределенность импульса и координат электрона принципиально невозможно.

Математически принцип неопределенности для частицы, движущейся в трехмерном пространстве, выражается тремя неравенствами:

Dx×Dp_x ³ h

Dy×Dp_y ³ h

Dz×Dp_z ³ h

где Dа и Dр_а неопределенности координат и проекций импульса на координатные оси, h = = 1,05×10^-34 Дж×с.

Из принципа неопределенности вытекает несколько важных выводов, необходимых для правильного понимания особенностей микромира:

1. Микрочастица не имеет детерминированной (строго определенной) траектории.

2. В микромире инструмент наблюдения взаимодействует с объектом наблюдения, изменяя его характеристики.

3. Модель атома должна быть вероятностной. Следует отказаться от попыток определить точные значения характеристик микрочастицы (координат, импульса, энергии и т.) и попытаться установить их вероятные значения.

2. Принцип корпускулярно-волнового дуализма (Луи де Бройль, 1924 г.) - любому движущемуся материальному объекту можно поставить в соответствие волновой процесс. Уравнение де Бройля легко выводится для электромагнитного излучения, которое одновременно можно рассматривать как волну и как поток элементарных частиц - фотонов.

Если энергия волны определяется уравнением Планка Е = hn (n - частота излучения), а энергия частицы уравнением Эйнштейна E = mc² (m - масса фотона, с - скорость света), то согласно принципу де Бройля hn = mc². Частота излучения определяется формулой n = с/l (l -длина волны), следовательно l = h/mс.

Обобщая данное выражение на любой движущийся материальный объект, получаем:

Из принципа де Бройля вытекает вторая особенность квантовой механики - вероятность нахождения электрона в каждой точке околоядерного пространства должна подчиняться волновым законам.

Квантовая механика постулирует существование некой специальной функции, с помощью которой могут быть установлены вероятные значения всех характеристик (координат, импульса, энергии и т.д.) электрона или иной микрочастицы, определяющих ее состояние. Эта функция обозначается греческой буквой y (пси) и называется волновой функцией или пси-функцией. Волновая функция не имеет простого физического смысла, однако, как было показано М. Борном, четкий физический смысл имеет ее квадрат. Величина y² в какой-либо точке пространства прямо пропорциональнавероятности нахождения (dW) частицы в бесконечно малом элементе объема (dV), включающем эту точку.

dW ~ y²dV

Физический смысл квадрата волновой функции налагает определенные ограничения на свойства y - функции. Так, она должна быть конечна, непрерывна и однозначна. Действительно, вероятность нахождения электрона в той или иной точке всегда конечна и не может принимать несколько значений. Там, где электрон не может находиться (например, на бесконечно большом расстоянии от ядра), волновая функция должна обращаться в нуль. Волновая функция, удовлетворяющая условию

называется нормированной. Условие нормировки означает, что вероятность нахождения электрона в бесконечно большом объеме равна единице, т.е., что этот электрон где-то находится.

Для выражения вероятностных значений характеристик микрочастицы через волновую функцию квантовая механика использует математический аппарат теории операторов. Оператором называется символ, показывающий, что надо сделать с данной функцией, чтобы превратить ее в некую другую функцию, т.е. оператор - это набор правил, ставящий в соответствие одной функции другую. Так, например, алгебраический оператор ln показывает, что действие его на функцию f(x) сводится к нахождению функции F(x), удовлетворяющей условию

f(x) = e^F(x)

Оператор частного дифференцирования показывает, что функцию f(x,y...) нужно дважды продифференцировать по x, полагая остальные переменные постоянными.

Квантовая механика утверждает, что каждой физической характеристике микрочастицы b соответствует определенный оператор . Так оператором координаты электрона является сама координата ( = x), импульсу электрона отвечает оператор импульса =- 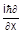, где i = . Более сложным является оператор полной энергии (оператор Гамильтона или гамильтониан):

где m - масса электрона, U - его потенциальная энергия, Ѳ (читается "набла квадрат") - оператор Лапласа (лапласиан)

действие которого предполагает суммирование вторых частных производных, взятых по всем координатам микрочастицы.

Чтобы найти вероятное значение того или иного свойства, нужно подействовать соответствующим оператором на y-функцию, результат умножить на y-функцию и проинтегрировать полученное выражение по всему объему:

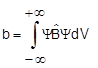
Это утверждение имеет характер постулата, но без каких-либо исключений подтверждается опытом.

Набор волновых функций, необходимых для определения вероятностных значений свойств частицы, находят, решая для нее основное уравнение квантовой механики (Э. Шредингер, 1926).

где - оператор полной энергии (оператор Гамильтона, гамильтониан), Е - полная энергия системы.

Кажущаяся простота уравнения исчезает при раскрытии гамильтониана, который включает кинетическую часть и потенциальную энергию электронов (U):

Если учесть, что сама по себе волновая функция имеет довольно сложный вид, то становится понятным, почему решение уравнения Шредингера связано с колоссальными сложностями. Строго оно может быть решено только для одноэлектронных частиц, например, для атома водорода. В то же время, решение уравнения Шредингера даже для столь простых систем привело к двум интересным следствиям:

1. Решения имеют дискретный характер и представляют собой набор волновых функций и соответствующих им дискретных (квантованных) значений энергии атома.

2. Волновые функции включают целочисленные параметры, изменяющиеся на единицу - квантовые числа. Поэтому орбитали атомы водорода можно качественно описать с помощью набора квантовых чисел. Каждое квантовое число играет важную роль, обеспечивая квантование (дискретность) определенной физической величины.

Главное квантовое число (n). Изменяется дискретно, принимая значения 1,2,3...¥. Главное квантовое число характеризует прежде всего энергетический уровень электрона, энергия которого определяется следующим выражением:

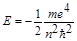
Поскольку масса (m) и заряд электрона постоянны, энергия последнего зависит только от квантового числа. Как следует из приведенношо выше уравнения, максимальное значение Е соответствует n = ¥ и равно нулю. Эта энергия отвечает удалению электрона на бесконечно большое расстояние от ядра, т.е. ионизации атома водорода. Все остальные разрешенные значения энергии отрицательны; минимальное из них составляет

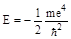= -1,31×10³ кДж/моль

Главное квантовое число характеризует также размеры орбитали. Совершенно очевидно, что орбиталь не имеет строгих размеров в обычном понимании этого слова, так как электрон с разной вероятностью может находиться в любой точке пространства. Под размерами орбитали в квантовой механике понимают определенную вероятностную характеристику атома. Поместим ядро атома в центр координат, разобьем окружающее его пространство на множество тончайших концентрических сферических слоев. Объем такого слоя, отстоящего от ядра на расстояние r, будет равен 4pr²dr, где dr - толщина слоя. Тогда в соответствии с физическим смыслом квадрата волновой функции вероятность нахождения электрона в таком слое составит

dW = 4pr²y²dr

Если построить кривую зависимости 4pr²y² от r, то мы получим график функции радиального распределения вероятности. Примеры таких кривых приведены на рис. 1. Эти кривые имеют один или несколько максимумов, отвечающих расстояниям, на которых электрон находится наиболее часто. Чем выше максимум, тем больше вероятность появления электрона на отвечающем этому максимуму расстоянии от ядра. Если на кривой 4pr²y² = f(r)максимумов несколько, то самый высокий из них будет расположен тем дальше от ядра, чем больше значение главного квантового числа.

Рис. 1. Кривые радиального распределения вероятности нахождения электронов для некоторых

орбиталей атома водорода

Орбитальное квантовое число (l). Для заданного значения n принимает целочисленные значения от 0 до (n-1). Значение l обозначается буквами в следующем порядке

l 0 1 2 3 4 5

Обозначение s p d f g h

Соответственно, орбитали, для которых l= 0 называются s-орбиталями, l= 1 - р-орбиталями и т.д.

Орбитальное квантовое число характеризует энергетические подуровни атома, включающие орбитали с одинаковыми значениями n и l. Сколько значений принимает l в пределах заданного значения n, столько подуровней включает данный энергетический уровень. Так, например, второй энергетический уровень, для которого n = 2, а l принимает значения 0 и 1, имеет два подуровня, обозначаемые символами 2s и 2p.

Заметим, что для атома водорода подуровни одного уровня имеют одинаковую энергию, в случае многоэлектронных атомов подуровни отвечают разным энергиям.

От орбитального квантового числа зависят также значения, которые может принимать орбитальный момент импульса электрона. Орбитальным моментом импульса называется векторное произведение радиус-вектора и импульса электрона:

Как всякий вектор, момент импульса характеризуется абсолютной величиной (модулем M_l) и направлением, определяемым проекциями M_l на координатные оси. Орбитальное квантовое число квантует значения M_l в соответствии с уравнением

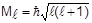
Так, для s-подуровней модуль момента импульса равен нулю, для всех р-подуровней - и т.д.

Орбитальное квантовое число определяет форму граничной поверхности орбитали. Так, все s-орбитали имеют сферическую форму, р-орбитали - форму гантели (объемной восьмерки); форма d-орбиталей - либо объемная четырехлепестковая розетка, либо гантель в кольце. Примеры формы орбиталей, отвечающих различным значениям l, приведены на рис. 2.

Главное и орбитальное квантовые числа совместно обуславливают форму кривой функции радиального распределения вероятности: число максимумов на этой кривой равно разности n-l. Например, для подуровня 1s (n = 1, l = 0) кривая радиальной вероятности имеет один максимум, для подуровня 2s (n = 2, l= 0) - два максимума, для подуровня 2p (n = 2, l= 1) - один максимум и т.д. (рис. 1).

Магнитное квантовое число (m_l). В пределах заданного значения l магнитное квантовое число принимает значения 0, ±1, ±2, ±3...±l. Это квантовое число определяет ориентацию вектора в пространстве, квантуя проекцию вектора на одну из координатных осей, например, на ось z:

M_lz =

Определению проекций на другие координатные оси препятствует принцип неопределенности, так как, если бы это было возможно, было бы установлено точное значение момента импульса электрона.

Характеризуя направление орбитального момента импульса, магнитное квантовое число тем самым определяет ориентацию электронной орбитали в пространстве. Сколько значений принимает m_l для заданного значения l, столько орбиталей, по-разному ориентированных в пространстве, возможно для данного подуровня (рис. 2). Так, для s-подуровня m_l принимает одно значение (m_l= 0), соответственно чему s-орбиталь может быть ориентирована в пространстве одним способом, а s-подуровень включает лишь одну орбиталь. В случае р-подуровня m _l имеет три значения (0, ±1) и три р-орбитали этого подуровня ориентируются в пространстве тремя разными способами: одна из них вытянута по оси x (орбиталь p_x), другая по оси у (орбиталь p_y), третья по оси z (орбиталь p_z) (рис. 2).

d-Подуровень включает пять орбиталей (m_l = 0, ±1, ±2), ориентированных относительно координатных осей пятью различными способами: орбиталь представляет собой вытянутую по оси z гантель, продетую в кольцо вращения (тороид) (рис. 2). Орбиталь - четырехлепестковая розетка, ориентированная по осям x и y. Орбитали d_xy, d_xz, d_yz имеют такую же форму, но ориентированы по биссектрисам соответствующих координатных углов. Знаками (+) и (-) на рис. 2 указан математический знак волновой функции для разных областей пространства.

Орбитали одного уровня, отличающиеся значениями m_l, имеют одинаковые энергии. Число таких орбиталей определяет степень вырождения подуровня. Так, s-подуровень не вырожден, р-подуровень трехкратно вырожден, степень вырождения для d- и f-подуровней равна соответственно пяти и семи. В общем случае степень вырождения определяется следующей формулой:

С.В. = 2l + 1

При помещении атома в электрическое или магнитное поле, энергии орбиталей с одинаковыми значениями l, но разными значениями m_l становятся неодинаковыми, так как эти орбитали по-разному ориентированы относительно направления поля. Происходит снятие вырождения, соответственно чему линии в атомном спектре расщепляются.

Рис. 2. Форма граничной поверхности s-, p- и d-орбиталей

Квантовые числа n, l и m_l квантуют физические характеристики электрона, связанные с его поступательным движением. Однако электрон, кроме орбитального момента импульса, имеет еще и собственный момент импульса (спин), связанный с квантово-механическим аналогом вращательного движения, что обеспечивает четвертую степень свободы электрона. Как указывалось выше, для квантования орбитального момента импульса необходимы два квантовых числа (l и m_l); аналогично для квантования собственного момента импульса так же нужны два квантовых числа - спиновое (s), квантующее модуль момента (M_S), и магнитное спиновое (m_S), квантующее направление вектора . Экспериментально установлено, что в сильных электрических и магнитных полях любая орбиталь проявляет свойства двух кратно вырожденной. Соответственно,

С.В. = 2s + 1; s = 1/2

Таким образом, квантовое число s является полуцелым и одинаково для всех электронов. Проекция собственного момента импульса на направление магнитного поля имеет два значения, соответственно чему магнитное спиновое квантовое число принимает значения +1/2 (a-спин, ­) и -1/2 (b-спин, ¯).

Найденные значения s и m_S позволяют квантовать характеристики собственного момента импульса электрона:

;

Поиск по сайту: