Операции со сложной учетной ставкой. Учет по сложной учетной ставке.В практике учетных операций иногда применяют сложную учетную ставку (compound discount rate)

Учет по сложной учетной ставке. В практике учетных операций иногда применяют сложную учетную ставку (compound discount rate). В этих случаях процесс дисконтирования происходит с замедлением, так как каждый раз учетная ставка применяется не к первоначальной сумме (как при простой учетной ставке), а к сумме, уже дисконтированной на предыдущем шаге во времени. Дисконтирование по сложной учетной ставке осуществляется по формуле

P = S (1 - d) ⁿ, (2.14)

где d — сложная годовая учетная ставка.

Пример 2.10. Финансовый инструмент на сумму 5 млн. руб., срок платежа по которому наступает через пять лет, продан с дисконтом по сложной учетной ставке 15% годовых. Какова сумма дисконта?

Р = 5 000 000(1 - 0,15)⁵ = 2 218 526,56;

D = S - P = 2 781 473,44 руб.

Следует отметить, что дисконтирование по сложной учетной ставке выгоднее для должника, чем дисконтирование по простой учетной ставке. Сказанное становится понятным при сравнении формул для дисконтных множителей: (1 - nd_s) и (1 - d) ⁿ; здесь d_s — простая, d — сложная учетная ставка. Согласно первой формуле значение дисконтного множителя равномерно уменьшается по мере роста n и достигает нуля при n = l/ d_s. Согласно второй множитель экспоненциально уменьшается и достигает нуля лишь в пределе, при n =∞. Величины дисконтных множителей при применении простой и сложной учетной ставки (w_s, w) показаны на рис. 2.5.

Номинальная и эффективная учетная ставка. По аналогии с номинальной и эффективной ставкой процентов введем понятия "номинальная" и "эффективная учетная ставка". Обозначим номинальную учетную ставку как f. Пусть дисконтирование производится не один, a m раз в году, т.е. каждый раз по ставке f / m. В этом случае

P = S (l - f/m) ^mn, (2.15)

где f — номинальная годовая учетная ставка (nominal discount rate).

Эффективная учетная ставка характеризует результат дисконтирования за год. Она находится из равенства

(1 - d) = (1 - f / m) ^m,

откуда

d = 1 - (1 - f/m) ^m.

Для одних и тех же условий операции эффективная учетная ставка меньше номинальной.

Пример 2.11. По данным примера 2.10 определим сумму, полученную при поквартальном дисконтировании по номинальной учетной ставке 15%. В данном случае f = 0,15; т = 4.

P = 5 000 000(1 - 0,15/4)²⁰ = 2 328 009,61 руб.

Эффективная учетная ставка составит

d = l - (1 - 0,15/4)⁴ = 0,14177, или 14,177%.

Наращение по сложной учетной ставке. Выше мы имели дело с наращением на основе сложной ставки процентов (ставки наращения). Однако это не единственный возможный метод. Иногда наращение достигается и с помощью сложной учетной ставки. Из формул (2.14) и (2.15) следует:

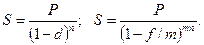(2.16) (2.17)

Множитель наращения при использовании сложной ставки d, очевидно, равен .

Поиск по сайту: