Долгосрочные ссуды

Очевидно, что способ погашения долгосрочной задолженности оказывает заметное влияние на эффективность соответствующей финансовой операции для кредитора. В данном параграфе кратко рассмотрены методы оценивания ПД долгосрочных ссуд для двух случаев: 1) когда проценты погашаются последовательными платежами, а основная сумма долга выплачивается в конце срока и 2) когда долг и проценты погашаются последовательно на протяжении всего срока ссуды. В обоих случаях предусматривается выплата комиссионных.

Ссуды с периодической выплатой процентов. Если комиссионные не выплачиваются, то доходность равна годовой ставке сложных процентов, эквивалентной любым применяемым в сделке процентным ставкам. Ситуация усложняется, если имеется еще один источник дохода для кредитора — комиссионные. Пусть ссуда D погашается через n лет, проценты по простой процентной ставке i выплачиваются регулярно в конце года. Проценты в таком случае равны Di. Должнику с учетом комиссионных выдается ссуда в размере D (1 - g). Балансовое уравнение, полученное дисконтированием всех платежей по неизвестной ставке i_Э, имеет вид:

Здесь v = (1 + i_Э)^-1, . Теперь это уравнение можно представить в виде функции от i_Э следующим образом:

Если проценты выплачиваются р раз в году, то

Задача, следовательно, заключается в нахождениикорня степенной функции.

Пример 9.10. На три года выдана ссуда в 1 млн. руб. под 10% годовых,проценты выплачиваются ежегодно. При выдаче ссуды сделана скидка в пользу владельца денег в размере 5%. В результате должник получил 950 тыс. руб. Для расчета искомой ставки i_Э сразу можно написать функцию от i_Э:

Решение, например, методом Ньютона - Рафсона или простым подбором дает i_Э = 1,12088. Таким образом, доходность операции для кредитора и соответственно цена кредита для должника в виде годовой ставки сложныхпроцентов равны 12,088%.

По-видимому, здесь уместно произвести проверкурезультата и описать процесс погашения ссуды исходяиз найденного значения процентной ставки. Итак, долг в размере 950 тыс. руб. вырастает за первый год до 950 х 1,12088 = 1064,84, после первой уплаты задолженность составит 964,68; на конец второго года имеем 964,84 х 1,12088 - 100 = 981,47 и, наконец, в последнем году сумма, подлежащая уплате, равна 981,47 х 1,12088 = 1100 тыс., руб. (см. рис. 9.1).

Ссуды с периодическими расходами по долгу. Пусть по ссуде периодически выплачиваютсяпроценты и погашается основной долг, причем сумма расходовпостоянна. Тогда балансовое уравнение для случая, когда платежи производятся вконце года, можно представить в виде

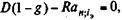
где R — ежегодная сумма по обслуживанию долга (срочная уплата). Поскольку (см. параграф 7.3), то

(9.18)

Аналогично для случая, когда погасительные платежи осуществляются р раз в году, находим

(9.19)

где и — коэффициенты приведения годовой и р -срочной ренты, члены которой равны расходам должника по ссуде.

Пример 9.11. Пусть в примере 9.10 задолженность погашается равными платежами. Все остальные условия не изменяются. В этом случае согласно (9.18)

= a _3;10(l - 0,05) = 2,48685 x 0,95 = 2,36251.

Расчет i_Э по заданному значению = 2,36251 можно легко осуществить с помощью линейной интерполяции. Поскольку i_Э > 10%, то примем i_н = 12% и i_в = 13%. Находим следующие табличные значения коэффициентов приведения: a ₃.₁₂ = 2,38134, a _3;13 = 2,36115. Интерполяционное значение ставки

i_Э = 12 + (13 - 12) = 12,933%.

Нерегулярный поток платежей. Задолженность может быть погашена путем выплаты нерегулярного потока платежей: R ₁,..., R_n. Эффективность кредита при таком способе погашения определим на основе следующего уравнения, балансирующего вложения и отдачи:

(9.20)

где t_j — интервал от начала сделки до момента выплаты j -го погасительного платежа. Из условия сбалансированности сделки находим, применяя договорную ставку i, величину последнего взноса:

(9.21)

где q = 1 + i_Э;

T = T_j, T_j — срок от выплаты j -го платежа до конца сделки.

Продемонстрированный выше метод оценки показателя полной доходности на основе функции f (i_Э) применяется, в частности, при анализе облигаций и производственных инвестиций. В следующих главахмы обсудим эти проблемы.

Поиск по сайту: