 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Определение срока платежа и процентных ставок
При разработке условий финансовых операций часто сталкиваются с необходимостью решения обратных задач — расчета продолжительности ссуды или уровня процентной ставки. Для простых процентов эти задачи рассмотрены в гл. 1. Обратимся к операциям со сложными процентными ставками и решим уравнения, связывающие Р и S, относительно интересующих нас величин. Ниже приводятся полученные результаты.
Срок платежа. Приведем формулы расчета п для различных условий наращения процентов и дисконтирования. При наращении по сложной годовой ставке i и по номинальной ставке j соответственно получим:
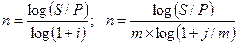. (2.23) (2.24)
При дисконтировании по сложной годовой учетной ставке d и по номинальной учетной ставке f
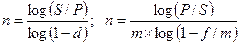. (2.25) (2.26)
При наращении по постоянной силе роста δ и по изменяющейся с постоянным темпом силе роста
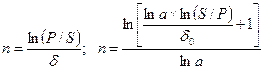. (2.27) (2.28)
Пример 2.15. За какой срок в годах сумма, равная 75 млн. руб., достигнет 200 млн. при начислении процентов по сложной ставке 15% раз в году и поквартально? По формулам (2.23) и (2.24) получим:
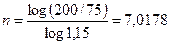года (7 лет и 6 дней),
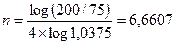года (6 лет и 241 день).
Величина процентной ставки. Приведем формулы для расчета ставок i, j, d, f, δ для различных условий наращения процентов и дисконтирования. Они получены при решении уравнений, определяющих S и Р, относительно искомых ставок.
При наращении по сложной годовой ставке процентов и по номинальной ставке процента т раз в году находим
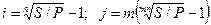. (2.29) (2.30)
При дисконтировании по сложной учетной ставке и по номинальной учетной ставке
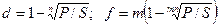. (2.31) (2.32)
При наращении по постоянной силе роста
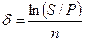. (2.33)
При наращении по изменяющейся с постоянным темпом силе роста
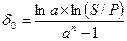. (2.34)
Пример 2.16. Сберегательный сертификат куплен за 100 тыс. руб., выкупная его сумма — 300 тыс. руб., срок — 2,5 года. Каков уровень доходности инвестиций в виде годовой ставки сложных процентов? По формуле (2.29) находим
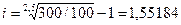, или 16,334%
Пример 2.17. Срок до погашения векселя равен двум годам. Дисконт при его учете составил 30%. Какой сложной годовой учетной ставке соответствует этот дисконт?
Применим формулу (2.31). По данным задачи Р/S = 0,7, откуда
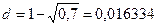, или 16,334%.
Поиск по сайту: