Непрерывные переменные потоки платежей

В предыдущей главе были обсуждены непрерывные потоки платежей. Однако там предполагалось, что годовая сумма R непрерывно и равномерно распределена в пределах года. Такой поток денежных поступлений или выплат не является единственно возможным. На практике, особенно при анализе инвестиций в производство, поток платежей может существенно изменяться во времени, в том числе и следуя какому-либо закону.

Если поток платежей непрерывен и описывается некоторой функцией R_t = f(t),то общая сумма поступлений за время n равна

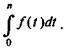
В этом случае наращенная сумма (при начислении процентов используется процентная ставка в виде силы роста) находится как

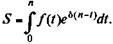
Современная стоимость такого потока определяется как

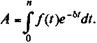
Для того чтобы рассчитать величины A и S, необходимо определить конкретный вид функции потока платежей и значения ее параметров. Ниже рассматриваются методы расчета современных стоимостей для двух видов функций — линейной и экспоненциальной. Наращенные суммы таких потоков легко определить исходя из соотношения:

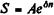(5.20)

Линейно изменяющийся непрерывный поток платежей. Функция потока:

R_t = R ₀ + at,

где r ₀ — начальный размер платежа, выплачиваемого в единицу времени, в котором измеряется срок ренты.

Современнаястоимость получена с помощью интегрирования функции потока платежей:

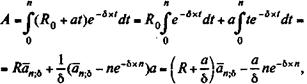(5.21)

где 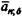— коэффициент приведенияпостоянной непрерывной ренты (см. формулу (4.48)).

Первый вариант записи результата интегрирования наглядно демонстрирует влияние начального размера платежа и приростов.

Пример 5.7. Намечается в течение трех лет увеличивать ежегодно выпуск продукции на 1 млрд. руб. Базовый уровень выпуска — 10 млрд. руб. Необходимо определить суммарный стоимостный объем выпуска с начислением процентов — сила роста 8%.

Для начала определим современную стоимость данного непрерывного потока поступлений:

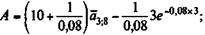
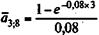= 2,66715; A = 30,5 млн. руб. Затем находимнаращенную сумму S = 30,5 х е ^0,08x3 = 38,8 млн. руб.

Практически важной является проблема оценки размера процентной ставки, если заданы все остальные параметры потока платежей.Оценка осуществляется с помощью метода Ньютона - Рафсона (см. формулу (4.41)). Необходимые для этого функции имеют следующий вид:

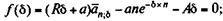(5.22)

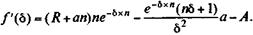(5.23)

Функция (5.22) получена путем простого преобразования (5.21); функция (5.23) — производная от (5.22).

Пример 5.8. Капиталовложения составят 1000 млн. руб., начальная отдача от них оценивается в сумме 300 млн. руб. в год. Предполагается, что отдача будет непрерывно увеличиваться в течение всего периода эксплуатации (пять лет) — по 10 млн. в год. Какова доходность инвестиций, измеренная в виде силы роста и годовой процентной ставки?

По условиям задачи: A = 1000, R = 300, а = 10, п = 5.Пусть первая оценка силы роста — 17%. По формулам (5.22) и (5.23) находим f (0,17) = 14,08; f' (0,17) = -525. Отсюда:

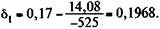
Проверка: по формуле (5.21) получим A = 1021. Иначе говоря, ставка несколько занижена. Выполним еще одну итерацию: f (0,197) = 4,1; f' (0,197) = 654.

Из этого следует:

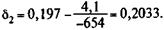
В этом случае A = 1000. Показатель доходности в виде годовой ставки сложных процентов i = e ^0,2033 - 1 = 0,2254, или 22,33% годовых.

Экспоненциальный рост платежей. Функция потока платежей:

R_t = R x e^qt, (5.24)

где q — непрерывный темп прироста платежей.

Современная величина такой ренты определяется следующим образом:

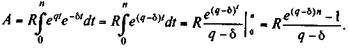(5.25)

Нетрудно найти зависимость непрерывных и дискретных темпов прироста и процентных ставок:

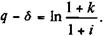(5.26)

Пример 5.9. Ожидается, что прирост доходов составит 5% в год. Какова современная стоимость и наращенная сумма потока доходов, если R = 100, i = 7%, n = 3 года. Из условий задачи следует:

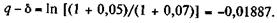
Таким образом,

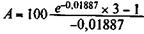= 291,5;

S = A (l + i)³ = 291,5 х 1,07³ = 357,17.

Поиск по сайту: