Чистый приведенный доход

Обычно в анализе производственных инвестиций одновременно применяют несколько измерителей эффективности. Один в качестве основного, другие как дополнительные. В качестве основного измерителя наибольшее распространение получил чистый приведенный доход (net present value, NPV). Обозначим этот показатель символом W. Данная величина характеризует общий абсолютный результат инвестиционной деятельности, ее конечный эффект. Под W понимают разность дисконтированных на один момент времени показателей дохода и капиталовложений. Если доходы и капиталовложения представлены в виде потока поступлений, то W равен современной величине этого потока. Как будет показано ниже, величина W является основой для определения других измерителей эффективности.

Итак, пусть поток поступлений характеризуется величинами R_t, причем эти величины могут быть как положительными, так и отрицательными. Тогда при условии, что ставка сравнения равна q, имеем

где R_t — размер члена потока платежей;

v — дисконтный множитель по ставке q (ставке сравнения). Влияние инвестиционных затрат и доходов от них на W можно представить в более наглядном виде

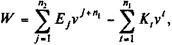(12.2)

где K_t — инвестиционные расходы в периоде t, t = 1, 2,..., п ₁;

E_J — доход в периоде j, j = 1, 2,..., n ₂;

n ₁ — продолжительность процесса инвестиций;

n ₂ — продолжительность периода отдачи от инвестиций.

В формуле (12.2) предполагается, что процесс отдачи идет сразу после окончания инвестиций. Если следует ожидать некоторого запаздывания (отдача начинается спустя п лет после начала осуществления проекта, т.е. n > n ₁), то вместо степени j + п ₁удисконтного множителя следует применить j + п.

Содержание показателя W легко понять из следующего примера. Пусть капиталовложения полностью осуществляются за счет заемных средств, причем ссуда выдана под ставку q. Наращение процентов на текущий доход также осуществляется по этой ставке. Тогда W представляет собой ожидаемый чистый доход, приведенный к начальному моменту времени.

Пример 12.1. Имеются варианты инвестиционного проекта, которые характеризуются следующими потоками платежей (для упрощения отнесем соответствующие показатели к концу года)

Варианты, как видим, существенно различаются между собой. При нормативе рентабельности (ставке сравнения) q = 10% получим:

W_A = -214,9 + 377,1 = 162,2; W_Б = -223,14 + 386,19 = 163,05.

Таким образом, если исходить из величины чистого приведенного дохода, то при принятой процентной ставке сравниваемые варианты в финансовом отношении практически равноценны.

Перейдем теперь к определению чистого приведенного дохода для случаев, когда отдачи от инвестиций и сами капиталовложения представляют собой последовательность платежей с установленными закономерностями изменений во времени. В этих случаях с помощью формул, полученных для современных величин рент (см. гл. 4,5), можно существенно упростить расчет W. Более того, создается возможность для развернутого анализа w иотносительных показателей эффективности, включая исследование влияния факторов. Пусть вложения и поступления равномерные и дискретные, причем доходы начинают поступать сразу после завершения вложений. Тогда W находим как разность современных величин двух рент:

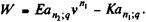
Здесь из современной величины отсроченной ренты (доход) вычитается современная величина немедленной ренты (инвестиции).

Пример 12.2. Инвестиции производятся поквартально по 0,25 млн. руб. на протяжении трех лет. Ожидаемая отдача оценена в размере 0,7 млн. руб. в год (поступления ежемесячные). Ренты, характеризующие вложения и отдачу, имеют следующие параметры: K = 1, n ₁ = 3, p ₁ = 4, Е = 0,7, n ₂ = 10, p ₂ = 12.

Пусть норматив рентабельности равен 10%, тогда находим

W = 0,7 x x v ³ - 0,25 x 4 x = 0,7 x 6,4213 x 0,7513 -- 2,5783 = 0,8 млн. руб.

Продолжим пример. Допустим теперь, что есть основание рассматривать вложения и отдачу как непрерывные процессы. Тогда

где 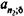— коэффициент приведения непрерывной ренты. Сила роста составит = ln1,1 = 0,09531. Окончательно получим

W = 0,7 х 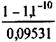х 1,1^-3 - 1 х = 0,78 млн. руб.

Пусть отдача от капиталовложений происходит не сразу после их завершения, а, скажем, через год. Тогда в рамках первоначального варианта постановки задачи (ежеквартальные затраты и ежемесячные поступления) получим:

W = 7 х х v ^-4 - 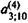= 0,5 млн. руб.

Таким образом, отсрочка на год отдачи от инвестиций заметно снизила чистую приведенную величину дохода.

Рассмотренные выше ситуации, разумеется, не исчерпывают все возможные случаи, с которыми можно столкнуться в практике. Так, совершенно необязательно, чтобы вложения и отдачи следовали одной и той же общей закономерности. Например, вложения могут быть периодическими (условия финансирования), а отдача может быть непрерывной (условия производства). Более того, один и тот же процесс в разных интервалах времени часто следует различным закономерностям — например, доход в периоде освоения или в периоде полного использования мощностей. Анализ в этих и других случаях должен учитывать особенности распределения инвестиций и доходов во времени. Некоторые из таких ситуаций будут рассмотрены нами при моделировании сложных инвестиционных процессов. Из приведенных выше выражений ясно, что абсолютная величина чистого приведенного дохода зависит от двух видов параметров. Первые характеризуют инвестиционный процесс, если так можно сказать, объективно. Они определяются производственным процессом. Ко второму виду следует отнести единственный параметр — ставку сравнения. Как уже говорилось, значение этой ставки — результат выбора, в определенном смысле это условная величина. В силу сказанного есть основание определять W нe для единственного значения q, а для некоторого диапазона значений ставки.

Зависимость w от q для случая, когда вложения осуществляются в начале процесса, а отдача примерно равномерная, иллюстрируется на рис. 12.1, где показано, что когда ставка сравнения достигает некоторого значения q_b, эффект инвестиции оказывается нулевым. Любая ставка, меньшая, чем q_b, соответствует положительной оценке W (содержание показателя q_b и методика его расчета рассматриваются ниже). На этом же рисунке показана область значений W для интервала размеров процентной ставки (q ₁ - q ₂). При иных закономерностях в распределении вложений и доходов график зависимости W от q может быть иным — в некоторых условиях W может неоднократно оказаться нулевым или вовсе не иметь нулевого значения.

Остановимся еще на одном важном свойстве показателя чистого приведенного дохода. Выше эта характеристика была определена путем приведения соответствующих сумм к началу инвестиционного процесса. Вместе с тем представляется возможной и практически важной оценка W на момент завершения процесса вложений или на иной момент времени, по каким-то причинам являющийся важным для исследователя.

Нетрудно доказать, что

W_t = W ₀(1 + q) ^t,

где W ₀ и W_t — величины чистого приведенного дохода, рассчитанные на начало инвестиционного процесса и некоторый момент t после него.

Разумеется, при сравнении нескольких проектов момент оценки должен быть общим для всех проектов. Следует также заметить, что предпочтительный вариант проекта остается таковым при любом выборе момента оценки.

Прежде чем мы закончим обсуждение свойств чистого приведенного дохода, остановимся еще на одной проблеме. Дело в том, что при высоком уровне ставки отдаленные платежи оказывают малое влияние на W. В силу этого различные по продолжительности периодов отдачи варианты могут оказаться практически равноценными по конечному экономическому эффекту. Например, при сравнении двух вариантов отдачи с одинаковой годовой суммой R = 200, но с разными сроками выплат (25 и 30 лет) при условии, что инвестиционные затраты к началу отдачи равны K = 1000, находим: при q = 15%для первого варианта W = 5460, для второго — 5570, т.е. пять дополнительных лет дают прирост менее 2% от размера ожидаемого эффекта.

Как было показано, проекты с длительной отдачей имеют незначительное преимущество, которое легко может быть перекрыто влиянием какого-либо менее существенного фактора. В то же время ясно, что при всех прочих равных условиях проект с более длительным периодом поступлений доходов предпочтительнее. В связи с необходимостью учета этого фактора в западной финансовой литературе обсуждаются некоторые дополнительные показатели, которые базируются на различных подходах к двум частям потока поступлений — в пределах срока окупаемости и за этими пределами. Те поступления, которые охватываются сроком окупаемости, рассматриваются как покрытие инвестиций, остальные поступления считаются чистым доходом, и на них дисконтирование не распространяется. Трудно найти какие-либо веские экономические обоснования для такой трактовки. Налицо лишь стремление усилить важность второй части потока платежей. С таким же успехом, вероятно, усиления второй части можно было бы достичь и иным путем, например умножая на какой-либо коэффициент и т.д. Дальнейшая модификация идет по линии еще большего внесения в методики расчета субъективных элементов. Так, теперь уже встречаются утверждения, что деление потока поступлений на основе срока окупаемости вовсе не обязательно. Это деление может осуществляться и любым иным путем. В частности, предлагалось просто выделять первые семь лет инвестиционного процесса.

Поиск по сайту: