Финансовая эквивалентность обязательств

В практике нередко возникают случаи, когда необходимо заменить одно обязательство другим, например с более отдаленным сроком платежа, досрочно погасить задолженность, объединить несколько платежей в один (консолидировать платежи) и т.п. В таких ситуациях неизбежно возникает вопрос о принципе, на котором должно базироваться изменение контракта. Таким общепринятым принципом является финансовая эквивалентность обязательств, которая предполагает неизменность финансовых отношений сторон до и после изменения контракта.

Эквивалентными считаются такие платежи, которые, будучи "приведены" к одному моменту времени (focal date), оказываются равными. Приведение осуществляется путем дисконтирования к более ранней дате или, наоборот, наращения суммы платежа (если эта дата относится к будущему). Если при изменении условий принцип финансовой эквивалентности не соблюдается, то одна из участвующих сторон терпит ущерб, размер которого можно заранее определить. По существу, принцип эквивалентности следует из формул наращения и дисконтирования, связывающих величины Р и S. Сумма Р эквивалентна S при принятой процентной ставке и методе ее начисления. Две суммы денег S ₁и S ₂,выплачиваемые в разные моменты времени, считаются эквивалентными, если их современные (или наращенные) величины, рассчитанные по одной и той же процентной ставке и на один момент времени, одинаковы. Замена S ₁ на S ₂в этих условиях формально не изменяет отношения сторон.

Пример 3.1. Имеются два обязательства. Условия первого: выплатить 400 тыс. руб. через четыре месяца; условия второго: выплатить 450 тыс. руб. через восемь месяцев. Можно ли считать их равноценными? Так как платежи краткосрочные, то при дисконтировании на начало срока применим простую ставку, равную, допустим, 20%, и получим:

= 375,00; 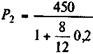= 397,06 тыс. руб.

Как видим, сравниваемые обязательства не являются эквивалентными при заданной ставке и в силу этого не могут адекватно заменять друг друга.

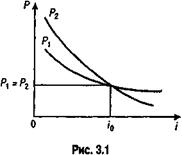
Сравнение платежей предполагает использование некоторой процентной ставки, и, следовательно, результат зависит от выбора ее величины. Однако, что практически весьма важно, такая зависимость не столь жестка, как это может показаться на первый взгляд. Допустим, что сравниваются два платежа S ₁и S ₂ со сроками п ₁и n ₂, измеряемыми от одного момента времени, причем S ₁ < S ₂и n ₁ < n ₂. Их современные стоимости Р ₁и Р ₂в зависимости от размера процентной ставки показаны на рис. 3.1.

С ростом i величина Р уменьшается, причем при i = i ₀наблюдается равенство Р ₁ = Р ₂. Для любой ставки i < i ₀ Р ₁ < Р ₂.В свою очередь, при i > i ₀ Р ₁> Р ₂.Таким образом, результат сравнения зависит от критического (барьерного) размера ставки, равного i ₀. Определим величину этой ставки. На основе равенства современных стоимостей сравниваемых платежей

находим

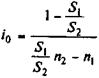. (3.1)

Из формулы (3.1) следует, что чем больше различие в сроках, тем больше величина i ₀ при всех прочих равных условиях. Рост отношения S ₁ /S ₂оказывает противоположное влияние.

Пример 3.2. Для данных примера 3.1 получим:

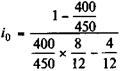= 0,428, или 42,8%.

Таким образом, соотношение Р ₂ > Р ₁справедливо для любого уровня процентной ставки, которая меньше 42,8%.

Если дисконтирование производится по сложной ставке, то критическую ставку найдем из равенства

Получим:

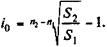(3.2)

Графическая иллюстрация зависимости Р от i приведена на рис. 3.1.

Пример 3.3. Сравниваются два платежа: 2 млн. руб. с выплатой через два года и 3 млн. руб. с выплатой через четыре года. Согласно формуле (3.2) критический уровень сложной процентной ставки равен:

i ₀ = 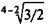- 1 = 0,2247, или 22,47%.

При любой ставке, которая меньше критической, современная стоимость первого варианта больше второго.

Поиск по сайту: