Консолидирование задолженности

Как уже было сказано выше, принцип эквивалентности применяется при различных изменениях условий выплат денежных сумм.

Общий метод решения подобного рода задач заключается в разработке так называемого уравнения эквивалентности (equation of value), в котором сумма заменяемых платежей, приведенных к какому-либо моменту времени, приравнивается к сумме платежей по новому обязательству, приведенных к той же дате. Для краткосрочных обязательств приведение осуществляется обычно на основе простых ставок, для средне- и долгосрочных — с помощью сложных ставок. Заметим, что в простых случаях часто можно обойтись без специальной разработки и решения уравнения эквивалентности.

Одним из распространенных случаев изменения условия является консолидация (объединение) платежей. Пусть платежи S ₁, S ₂,..., S_m со сроками n ₁, п ₂,..., п_т заменяются одним в сумме S ₀и сроком n ₀. В этом случае возможны две постановки задачи: если задается срок n ₀, то находится сумма S ₀, и наоборот, если задана сумма консолидированного платежа S ₀, то определяется срок n ₀. Рассмотрим обе постановки задачи.

Определение суммы консолидированного платежа. При решении этой задачи уравнение эквивалентности имеет простой вид. В общем случае, когда n ₁ < п ₂ <...< п_т, причем n ₁ < n ₀ < п_т, искомую величину находим как сумму наращенных и дисконтированных платежей. При применении простых процентных ставок получим:

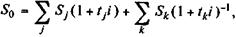(3.3)

где S_j — размеры объединяемых патежей со сроками n_i < n ₀;

S_k — размеры платежей со сроками n_k > n ₀;

t_j = n ₀ - n_j, t_k = n_k - n ₀.

В частном случае, когда n ₀ > п_т,

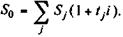(3.4)

Пример 3.4. Два платежа — 1 и 0,5 млн. руб. со сроками уплаты соответственно 150 и 180 дней — объединяются в один со сроком 200 дней. Пусть стороны согласились на применение простой ставки, равной 20% годовых. Консолидированная сумма долга составит:

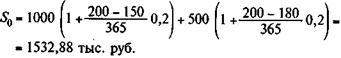
При объединении обязательств можно применить и учетные ставки. В этом случае при условии, что все сроки выплат пролонгируются, т.е. n ₀ > n_j,находим сумму наращенных по учетной ставке платежей:

В общем случае имеем

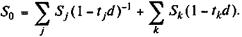
Здесь t_j, t_k имеют тот же смысл, что и выше.

Пример 3.5. Изменим одно условие в примере 3.4. Пусть консолидация платежей производится с помощью простой учетной ставки 20% (K = 360). Получим:

S ₀ = 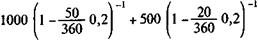= 1534,19 тыс. руб.

Консолидацию платежей можно осуществить и на основе сложных ставок. Вместо формулы (3.3) получим для общего случая (n ₁ < n ₀ < n_m)

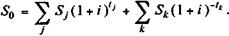(3.5)

Пример 3.6. Платежи в 1 и 2 млн. руб. со сроками уплаты два и три года объединяются в один со сроком 2,5 года. При консолидации используется сложная ставка 20%. Искомая сумма составит:

S ₀= 1000 х 1,2^0,5 + 2000 х 1,2^-0,5 = 2921,19 тыс. руб.

Определение срока консолидированного платежа. Если при объединении платежей задана величина консолидированного платежа S ₀, то возникает проблема определения его срока n ₀. В этом случае уравнение эквивалентности удобно представить в виде равенства современных стоимостей соответствующих платежей.

При применении простой ставки это равенство имеет вид:

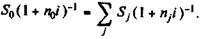
Отсюда

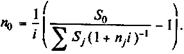(3.6)

Очевидно, что решение может быть получено при условии, что 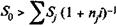, иначе говоря, размер заменяющего платежа должен быть больше суммы современных стоимостей заменяемых платежей. Заметим также, что искомый срок пропорционален величине консолидированного платежа.

Пример 3.7. Суммы в размере 10, 20 и 15 млн. руб. должны быть выплачены через 50, 80 и 150 дней соответственно. Стороны согласились заменить их одним платежом в размере 50 млн. руб. с отсрочкой выплаты долга.

Современная стоимость заменяемых платежей (обозначим эту величину через Р)при условии, что i = 10% и K = 365, составит:

Согласно (3.6) находим

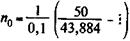= 1,404 года, или 512 дней.

Продолжим пример. Пусть теперь размер заменяющего платежа 45 млн. руб. Тогда срок заметно сократится и станет равным 0,264 года.

Перейдем к консолидации платежей на основе сложных процентных ставок. Уравнение эквивалентности запишем следующим образом:

Для упрощения дальнейшей записи примем

После чего находим

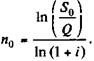(3.7)

Как видим, решение существует, если соблюдено условие S ₀ > Q. Для частного случая, когда S ₀ = 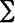S_j,при определении срока консолидирующего платежа вместо формулы (3.7) иногда применяют средний взвешенный срок:

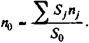(3.8)

Привлекательность этой формулы, помимо ее простоты, состоит в том, что она не требует задания уровня процентной ставки. Однако надо помнить, что она дает приближенный результат, который больше точного. Чем выше ставка i, тем больше погрешность решения по формуле (3.8).

Пример 3.8. Воспользуемся данными примера 3.6 и определим срок консолидированного платежа в сумме 3 млн. руб. Точное значение срока находим по формуле (3.7). Для этого сначала рассчитаем Q = 1 х 1,2^-2 + 2 х 1,2^-3 = 1,8518.

После чего находим п ₀= = 2,646 года.

Приближенное решение дает 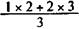= 2,667 года.

Поиск по сайту: