Средние процентные ставки

Проблема эквивалентности ставок в некоторых случаях может быть решена и с помощью расчета средних значений ставок. Если речь идет об одной финансовой операции, в которой размер ставки изменяется во времени, то все значения ставки можно обобщить с помощью соответствующей средней. Причем замена всех усредняемых значений ставки на среднюю ставку не должна изменить результаты наращения или дисконтирования.

Искомые средние получим при приравнивании множителей наращения друг к другу. Начнем с простой ставки. Пусть за периоды n ₁, n ₂,..., n_k начисляются простые проценты по ставкам i ₁, i ₂,..., i_k, тогда на основе равенства множителей наращения:

;

где N = — общий срок наращения;

— средняя ставка;

получим искомую среднюю:

Найденная характеристика представляет собой арифметическую среднюю взвешенную с весами, равными продолжительности отдельных периодов.

Аналогичным способом получим среднюю учетную ставку:

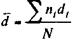
Пример 3.17. Контракт предусматривает переменную по периодам ставку простых процентов: 20; 22 и 25%. Продолжительность периодов: два, три и пять месяцев. Какой размер ставки приведет к аналогичному наращению исходной суммы? Находим среднюю:

Если усредняются переменные во времени ставки сложных процентов, то из равенства множителей наращения

следует:

(3.36)

Средняя в этом случае, как видим, вычисляется как взвешенная средняя геометрическая.

Пример 3.18. Допустим, для первых двух лет ссуды применяется ставка, равная 15%, для следующих трех лет она составляет 20%. Средняя ставка за весь срок ссуды равна

или 17,974%.

Рассмотрим теперь усреднение ставок, применяемых в нескольких однородных операциях, которые различаются суммой долга P_t и ставкой процента i_t. Искомые средние ставки находим из условия равенства соответствующих сумм после наращения процентов. Так, если применяются простые ставки и сроки этих операций одинаковы, то можно записать следующее исходное равенство:

(3.37)

Как видим, искомая ставка равна взвешенной арифметической средней; в качестве весов берутся размеры ссуд.

Усреднение сложных ставок для тех же условий достигается с помощью взвешенной степенной средней:

(3.38)

Пример 3.19. Выданы две ссуды: Р ₁ = 1 млн. руб., P ₂ = 2 млн. руб. Первая выдана под 20% годовых, вторая — под 30%, сроки ссуд одинаковы и равны полутора годам. Если ставки простые, то:

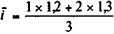= 0,2667.

Для сложных ставок находим:

= 0,2671.

Формулы (3.37) и (3.38) получены для частного случая, когда сроки ссуд одинаковы. В более общих случаях они, разумеется, не работают. Решение соответствующих задач возможно на основе методов, разработанных для так называемых потоков платежей. Эти методы обсуждаются в следующем разделе книги.

Раздел 2Потоки платежей

Поиск по сайту: