 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Льготные займы и кредиты
Грант-элемент. Предмет обсуждения в данном параграфе также связан с долгосрочными займами. Однако здесь они рассматриваются под другим углом зрения. Дело в том, что в ряде случаев долгосрочные займы и кредиты выдаются по тем или иным причинам под льготные для заемщика условия. Низкая (относительно ставки на рынке кредитов) процентная ставка в сочетании с большим его сроком и льготным периодом дают должнику существенную выгоду, которую можно рассматривать как субсидию. Кредитор в этих условиях несет некоторые потери, так как он мог бы инвестировать деньги на более выгодных условиях.
Проблема определения размера этой помощи обсуждалась в международных организациях и экономической литературе главным образом с позиции межстрановых сопоставлений — для сравнения размеров финансовой помощи, оказываемой ряду развивающихся стран. Однако проблема оценки последствий выдачи льготных займов имеет более общее значение, поскольку такие займы предоставляют и внутри страны. Сама проблема сводится к оценке грант-элемента.
Грант-элемент — это условная потеря заимодавца, которая связана с применением более низкой процентной ставки, чем ставка кредитного рынка. Грант-элемент определяется в двух видах: абсолютной и относительной величины.
Абсолютный грант-элемент рассчитывается как разность номинальной суммы займа и современной величины платежей по погашению займов. Проблема, как видим, сводится к выбору надлежащей ставки процента для расчета современной величины платежей. Рекомендации по выбору конкретного значения этой ставки весьма расплывчаты, обычно используют превалирующую на рынке долгосрочных кредитов ставку.
Размер абсолютного грант-элемента находим следующим образом:
W = D - G. (7.16)
Относительный грант-элемент:
 (7.17)
(7.17)
где W — абсолютный грант-элемент;
D — сумма займа;
G — современная величина платежей, поступающих в счет погашения займа, рассчитанная по реальной ставке кредитного рынка;
w — относительный грант-элемент.
Все переменные приведенных формул определяются условиями выдачи и погашения займа.
Выведем рабочие формулы для расчета W и w при условии, что долг и проценты выплачиваются в виде постоянных срочных уплат. Для анализа последствий выдачи льготных займов этого достаточно. Пусть заем выдан на n лет и предусматривает выплату процентов по ставке g. На денежном рынке аналогичные по сроку и величине займы выдаются по ставке i. В этом случае срочная уплата составит:
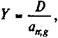 (7.18)
(7.18)
а современная величина всех выплат должника равна Yan ; i. В итоге согласно формуле (7.16):
 (7.19)
(7.19)
 (7.20)
(7.20)
где an;i, an;g — коэффициенты приведения постоянных годовых рент постнумерандо, определенные для процентныхставок i и g, i > g.
Очевидно, что наличие льготного периода увеличивает грант-элемент. Если в льготном периоде должник выплачивает проценты, то современная величина поступлений по долгу определяется как сумма двух элементов — современной величины процентных платежей в льготном периоде и современной величины срочных уплат в оставшееся время. Таким образом,
G = Dg x aL;i + Y х аn - L;l x vL,
где Y находится по формуле (7.18),
L — продолжительность льготного периода. После ряда преобразований получим:
 , (7.21)
, (7.21)
где an - L;i; an - L ; g — коэффициенты приведения постоянных рент со сроком n - L и ставками i и g;
vL — дисконтный множитель по ставке i.
Обсудим еще один возможныйвариант. Пусть в льготном периоде проценты начисляются, но не выплачиваются. Они присоединяются к основному долгу, который погашается в течение п - L лет. Условия такого займа более льготны для должника, чем при последовательной выплате процентов.
Срочные уплаты и их современная величина в данном случае равны:
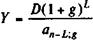 ; G = Y x an_L;i.
; G = Y x an_L;i.
Пример 7.12. Льготный заем выдан на 10 лет под 3,8%. Предусматривается погашение долга равными срочными уплатами. Известно, что обычная рыночная ставка для такого срока займа равна 8%.
В этом случае
w = l - 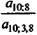 = 1 - 6,71008 х
= 1 - 6,71008 х  = 0,1809.
= 0,1809.
Допустим, что исходная сумма займа равна 10 млн. руб. Тогда абсолютный грант-элемент, или условная сумма потерь для кредитора и соответственно выгода для должника, составит:
W = 10 х 0,1809 = 1,809 млн. руб.
На основе этих выражений получим:
w = 1 -  = 1 -
= 1 -  .
.
Пример 7.13. Пусть заем примера 7.12 предусматривает трехлетний льготный период, в течение которого выплачиваются проценты. Для расчета относительного грант-элемента по формуле (7.21) находим: a 7;8 = 5,20637, а 7;3,8= 6,04667, a 3;8 = 2,5771, v 3 = 1,08-3 = 0,79383.
w = 1 - (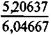 0,74383 + 0, 038 х 2,5771) = 0,2185.
0,74383 + 0, 038 х 2,5771) = 0,2185.
Если проценты в льготном периоде не выплачиваются, а присоединяются к основной сумме долга, то
w = 1 -  = 0,2356.
= 0,2356.
Грант-элемент, как было продемонстрировано выше, — условная обобщающая характеристика льготности займа (потерь заимодавца и выигрыша должника). Сумма, которая равна грант-элементу, существенно зависит от принятой при ее определении процентной ставки. График зависимости относительных потерь от соотношения процентных ставок показан на рис. 7.1 для сроков займа пять и десять лет без льготного срока, g = 5%.

Беспроцентный заем. Предельным случаем льготного займа является беспроцентный заем. Выдача такого займа связана с потерями, которые определим, полагая, что соответствующие средства можно было бы разместить под проценты по рыночной ставке i. Условия беспроцентного займа могут предусматривать льготный период, в течение которого погасительные платежи не поступают (отсрочка погашения).
Пусть долг погашается равномерно, каждый год в сумме D/n постнумерандо. Современная величина погасительных платежей равна

Относительная величина потерь, которую также можно назвать относительным грант-элементом, находится как
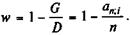 (7. 22)
(7. 22)
Наличие отсрочки, естественно, увеличивает потери для кредитора:
 (7. 23)
(7. 23)
Пример 7.14. Беспроцентный заем предоставлен на десять лет. Допустим, что на кредитном рынке средний размер ставки для такого срока составляет 10%. Для указанных условий находим
w = 1 -  = 1 -
= 1 - 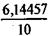 = 0,3855.
= 0,3855.
Выдача такого займа равнозначна субсидии, равной 38,55% суммы займа.
Если предусматривается трехлетний период отсрочки, то
w = l -  1,1-3 = 0,47732.
1,1-3 = 0,47732.
Значения относительных потерь в процентах для некоторых сроков беспроцентных займов без отсрочки и ряда уровней рыночных процентных ставок приведены в табл. 7.9.
Таблица 7.9
| Срок займа | i,% | ||||||
| 13,4 | 19,2 | 22,8 | 26,1 | 30,8 | 37,7 | 43,6 | |
| 15,8 | 22,4 | 26,4 | 30,1 | 35,3 | 42,7 | 48,9 | |
| 20,1 | 28,2 | 32,9 | 37,2 | 42,9 | 50,9 | 57,3 | |
| 24,2 | 33,3 | 38,6 | 43,2 | 49,3 | 57,4 | 63,7 | |
| 27,9 | 37,9 | 43,5 | 48,4 | 54,6 | 62,7 | 68,6 |
Как следует из таблицы, уже при пятнадцатилетнем сроке и ставке в 10% кредитор теряет почти 50% суммы долга.
Поиск по сайту: