Ренты с постоянным относительным приростом платежей

Рассмотрим ситуацию, когда платежи изменяют свои размеры во времени с постоянным относительным приростом, т.е. в геометрической прогрессии. Поток таких платежей состоит из членов R, Rq, Rq ²,..., Rq^{n -1} (где q — знаменатель прогрессии или темп роста). Пусть этот ряд представляет собой ренту постнумерандо. Тогда ряд дисконтированных платежей состоит из величин Rv, Rqv ²,..., Rq^{n- 1} vⁿ. Получена геометрическая прогрессия с первым членом Rv и знаменателем qv. Сумма членов этой прогрессии равна:

(5.14)

Пусть теперь q = 1 + k, где k — темп прироста платежей. Заметим, что прирост может быть как положительным (k > 0), так и отрицательным (k < 0). После простых преобразований получим:

(5.15)

Наращенная сумма ренты находится как

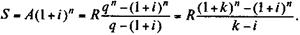(5.16)

Пример 5.3. Несколько изменим условия задачи 5.1. Пусть теперь члены ренты увеличиваются каждый год на 12% (k = 0,12). В этом случае:

= 93,448 млн руб.;

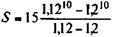= 578,604 млн руб.

Допустим теперь, что платежи уменьшаются во времени с темпом прироста минус 10% в год (k = -0,1), тогда:

S = 47,184 x 1,2¹⁰ =292,151 млн. руб.

Для рент пренумерандо получим:

Влияние изменения платежей установить в виде простой зависимости от q не удается, поэтому определим его как разность соответствующихсовременныхстоимостей или наращенных сумм.

Пример 5.4. Современная стоимость ренты с учетом ежегодного прироста на 10% впримере 5.3 равна 93,448 млн. руб. Современная стоимость постоянной ренты (без приростов ее членов) — 62,887 млн. руб. Таким образом, влияние приростов платежей определяется как 93,448 - 62,887 = 30,561 млн. руб.

Представляет некоторый практический интерес соотношение эквивалентности между абсолютным и относительным приростом членов рент. Технически удобнеенайти такое значение абсолютного прироста а, при котором величина современной стоимости равна A_q при заданном значении q. Методику получения искомого показателя нетрудно понять при рассмотрении рис. 5.2.

Из равенства показателей современных стоимостей потоков платежей с постоянными абсолютными и относительными приростами А_а = А_q следует:

Отсюда:

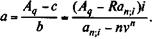(5.17)

Пример 5.5. В примере 5.3 при ежегодном относительном приросте платежей, равном 12%, современная стоимость потока платежей составляет 93,448 млн. руб. Какой должен быть ежегодный абсолютный прирост, который не изменит величину современной стоимости? Согласно формуле (5.17) получим:

Иначе говоря, ежегодный прирост платежей в сумме 2,371 млн. руб. эквивалентен (если принять во внимание весь срок) относительному приросту, равному 12%. Сказанное справедливо при условии, что все остальные условия сохраняются (R = 15, n = 10,

i = 20%).

p -срочная рента с постоянными относительными изменениями членов.

Пусть платежи производятся не один, a p раз в год постнумерандо, проценты начисляются раз в год по ставке i. В этом случае последовательность платежей представляет собой геометрическую прогрессию: R, Rq,..., Rq^{n -1}, где q — темп роста за период. Начислим проценты и суммируем результат, получим:

(5.18)

Для современной величины такой ренты находим:

(5.19)

Пример 5.6. Пусть, как и в других примерах главы, R = 15, n = 10, i = 20%. Предположим, что платежи увеличиваются с каждым полугодием на 6%. Тогда наращенная сумма и современная стоимость ренты составят:

=1263,052 млн руб.; 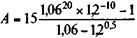= 203,990 млн руб.

Поиск по сайту: