 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Страхование жизни
Для начала рассмотрим самый простой случай личного страхования — страхование на дожитие (pure endowment), которое можно рассматривать как упрощенный вариант пенсионного страхования — страхование одной пенсионной выплаты. Строго говоря, здесь не возникает потребность в страховом аннуитете. Однако обсуждение применяемой методики окажется полезным далее. Итак, человек в возрасте х лет договаривается со страховой организацией о том, что при достижении им 60 лет он получит R рублей. Для определения размера премии найдем математическое ожидание суммы страховки, дисконтированной на срок страхования, т.е. на 60 лет:
60- xEx = R 60- xpxv 60- x
где 60- xpx - вероятность лицу в возрасте х лет дожить до 60 лет.
В общем виде с использованием коммутационной функции Dx получим:
 (6.7)
(6.7)
Влияние принятой процентой ставки здесь очевидно. Чем она выше, тем меньше премия.
Пример 6.2. Необходимо найти стоимость страхования на дожитие до 60 лет мужчины в возрасте 40 лет. Если расчет основывать на процентной ставке, равной 9%, то согласно формуле (6.7) получим:
20 Ex =  = R x 0,13239.
= R x 0,13239.
Премия здесь составляет чуть больше 13% страховой суммы. Полученная величина представляет собой нетто-ставкустрахования на дожитие, т.е. ставку, определенную из условия эквивалентности обязательств страхователя и страховщика. Напомним, что она не учитывает расходов страховщика на ведение дела.
Для того чтобы лучше понять смысл полученных результатов, предположим, что число застрахованных на дожитие равно 1000 человек, а страховая сумма равна 1 млн. руб. Таким образом:
| Число застрахованных | |
| Премия от одного застрахованного | 132390руб. |
| Общая сумма премии | 132 390 тыс. руб. |
| Сумма с процентами за 20 лет | 741 980 тыс. руб. |
| Количество доживших до 60 лет | 742 (741,198) |
| Общая сумма выплат | 742 000 тыс. руб. |
Как видим, наблюдается полная сбалансированность между взносами и выплатами, демонстрирующая соблюдение принципа эквивалентности обязательств страхователей и страховщика (небольшая разница объясняется округлением числа доживших).
Приведенный пример иллюстрирует действие принципа солидарной ответственности страхователей. Дело в том, что страхователь, доживший до 60 лет, часть денег получил за счет тех страхователей, которые не дожили до обусловленного возраста. В самом деле, если бы оговоренную сумму (1 млн. руб.) он обеспечивал самостоятельно (без солидарной ответственности всех участников), то ему необходимо было внести не 132 тыс. руб., а 178 тыс. руб.
Как было показано, в разовом страховании на дожитие страховые аннуитеты не применялись, однако в пенсионном страховании (которое фактически представляет собой многократно повторяемое страхование на дожитие) такие аннуитеты являются исходным материалом для расчета тарифов или размеров пенсий. Об этом более подробно будет сказано в следующем параграфе.
Обратимся теперь к страхованию жизни. Страховая сумма, равная S, выплачивается в случае смерти застрахованного. Допустим, страховой договор заключается в возрасте х лет. Если застрахованный умрет на первом году страхования, а выплата страховой суммы производится в конце этого года, то с учетом вероятности страхового случая современная величина выплаты (на момент заключения контракта) составит qxvS, если страховой случай наступит во втором году, то аналогичная величина равна 2 qxv 2 S и т.д.
Единовременный нетто-тариф определим исходя из принципа эквивалентности обязательств. Искомая величина равна современной стоимости страхового аннуитета или математическому ожиданию суммы дисконтированных выплат. Необходимые для расчета вероятности определим по таблице смертности как dx / lx, dx+ 1/ lx,..., dw / lx. Искомая величина определяется как

Как видим, здесь дисконтируются члены страхового аннуитета. Умножим и разделим каждое слагаемое на vх и используем коммутационную функцию Dx, после чего получим:

Применив функцию Мх, находим:
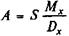 (6.8)
(6.8)
Пример 6.3. Найдем величину премии в виде доли от страховой суммы для сорокалетнего мужчины при немедленном пожизненном страховании жизни:
A =  = 0,14677 S.
= 0,14677 S.
Аналогичным путем находятся страховые аннуитеты и тарифы для других условий страхования жизни.
Поиск по сайту: