 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Измерение доходности облигаций
Доходность облигаций. Доходность облигаций характеризуется несколькими показателями. Различают купонную (coupon rate), тек у щую (current, running yield) и полную доходность (yield to maturity, redemption yield, yield).
Купонная доходность определена при выпуске облигации, и, следовательно, нет необходимости ее рассчитывать. Текущая доходность характеризует отношение поступлений по купонам к цене приобретения облигации. Этот параметр не учитывает второй источник дохода — получение номинала или выкупной цены в конце срока. Поэтому он непригоден при сравнении доходности разных видов облигаций. Достаточно отметить, что у облигаций с нулевым купоном текущая доходность равна нулю. В то же время они могут быть весьма доходными, если учитывать весь срок их "жизни".
Наиболее информативным является показатель полной доходности, который учитывает оба источника дохода. Именно этот показатель пригоден для сравнения доходности инвестиций в облигации и другие ценные бумаги. Итак, полная доходность, или, если применить старую коммерческую терминологию, ставка помещения, измеряет реальную эффективность инвестиций в облигацию для инвестора в виде годовой ставки сложных процентов. Иначе говоря, начисление процентов по ставке помещения на цену приобретения облигации полностью обеспечивает выплату купонного дохода и сумму для погашения облигации в конце срока.
Рассмотрим методику определения показателей доходности различных видов облигаций в той последовательности, которая принята выше при классификации облигаций по способу выплаты дохода.
Облигации без обязательного погашения с периодической выплатой процентов. Хотя подобного вида облигации встречаются крайне редко, знакомство с ними необходимо для получения полного представления о методике измерения доходности. При анализе данного вида облигаций выплату номинала в необозримом будущем во внимание не принимаем.
Введем следующие обозначения:
g — объявленная норма годового дохода (купонная ставка процента);
it — текущая доходность;
i — полная доходность (ставка помещения).
Текущая доходность находитсяследующим образом:
it = 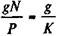 100. (11.2)
100. (11.2)
Если по купонам выплата производится р раз в году (каждый раз по ставке g/p), то и в этом случае на практике применяется «формула (11.2), хотя суммирование доходов, выплачиваемых в разные моменты времени, строго говоря, некорректно.
Поскольку купонный доход постоянен, то текущая доходность продаваемых облигаций изменяется вместе с изменением их рыночной цены. Для владельца облигации, который уже инвестировал некоторые средства, эта величина постоянна.
Перейдем к полной доходности. Поскольку доход по купонам является единственным источником текущих поступлений, то очевидно, что полная доходность у рассматриваемых облигаций равна текущей в случае, когда выплаты по купонам — ежегодные: i = it. Если же проценты выплачиваются р раз в году (каждый раз по норме g /p), то согласно (2.8) получим
 (11.3)
(11.3)
Пример 11.1. Вечная рента, приносящая 4,5% дохода, куплена по курсу 90. Какова финансовая эффективность инвестиции при условии, что проценты выплачиваются раз в году, поквартально (p = 4)?
i = it =  100 = 0,05; i =
100 = 0,05; i = 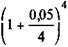 - 1 = 0,0509.
- 1 = 0,0509.
Облигации без выплаты процентов. Данный вид облигации обеспечивает ее владельцу в качестве дохода разность между номиналом и ценой приобретения. Курс такой облигации всегда меньше 100. Для
определения ставки помещения приравняем современную стоимость номинала цене приобретения:
Nvn = P, или vn =  ,
,
где n — срок до выкупа облигации. После чего получим
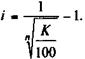 (11.4)
(11.4)
Пример 11.2. Корпорация X выпустила облигации с нулевым купоном с погашением через пять лет. Курс реализации — 45. Доходность облигации на дату погашения
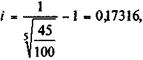
т.е. облигация обеспечивает инвестору 17,316% годового дохода.
Облигации с выплатой процентов и номинала в конце срока. Проценты здесь начисляются за весь срок и выплачиваютсяодной суммой (lump sum) вместе с номиналом. Купонного доходанет. Поэтому текущую доходностьусловно можно считать нулевой, поскольку соответствующие проценты получают в конце срока.
Найдем полную доходность,приравняв современную стоимость доходацене облигации:
(1 + g) nNvn = P, или  .
.
Из последней формулы следует, что
 (11.5)
(11.5)
Если курс облигации меньше 100, то i > g.
Пример 11.3. Облигация, приносящая 10% годовых относительно номинала, куплена по курсу 65, срок до погашения — три года. Если номинал и проценты выплачиваются в конце срока, то полная доходность для инвестора составит
i = 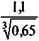 - 1 = 0,26956, или 26,956%.
- 1 = 0,26956, или 26,956%.
Облигации с периодической выплатой процентов и погашением номинала в конце срока. Этот вид облигаций получил наибольшее распространение в современной практике. Для такой облигации можно получить все три показателя доходности — купонную, текущую и полную. Текущая доходность рассчитывается по полученной выше формуле (11.2). Что касается полной доходности, то для ее определения необходимо современную стоимость всех поступлений приравнять цене облигации. Дисконтированная величина номинала равна Nvn. Поскольку поступления по купонам представляют собой постоянную ренту постнумерандо, то член такой ренты равен gN, а современная ее стоимость составит gNan;i (если купоны оплачиваются ежегодно) и 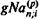 , если эти выплаты поизводятся р раз в году (каждый раз по ставке g/p). В итоге получим следующие равенства:
, если эти выплаты поизводятся р раз в году (каждый раз по ставке g/p). В итоге получим следующие равенства:
для облигации с годовыми купонами
 (11.6)
(11.6)
Разделив на N, находим
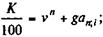 (11.7)
(11.7)
для облигации с погашением купонов по полугодиям и поквартально получим
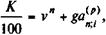 (11.8)
(11.8)
где  — коэффициент приведения p -срочной ренты (р = 2, р = 4).
— коэффициент приведения p -срочной ренты (р = 2, р = 4).
Во всех приведенных формулах vn означает дисконтный множитель по неизвестной годовой ставке помещения i.
В зарубежной практике, однако, для облигаций с полугодовыми и квартальными выплатами текущего дохода для дисконтирования применяется годовая номинальная ставка помещения, причем число раз дисконтирования в году обычно принимается равным числу выплат купонного дохода. Таким образом, исходное для расчета ставки помещения равенство имеет вид
 (11.9)
(11.9)
где i — номинальная годовая ставка;
рп — общее количество купонных выплат; g — годовой процент выплат по купонам.
При решении приведенных выше равенств относительно неизвестной величины i сталкиваются с такими же проблемами, что и при расчете i по заданной величине коэффициента приведения ренты — см. параграф 4.5. Искомые значения ставки помещения рассчитываются или с помощью интерполяции, или каким-либо итерационным методом.
Оценим i с помощью линейной интерполяции:
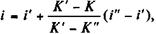 (11.10)
(11.10)
где i' и i" — нижнее и верхнеезначения ставки помещения, ограничивающие интервал, в пределах которого, как ожидается, находится неизвестное значение ставки;
K', K" — расчетные значения курса соответственно для ставок i', i". Интервал ставок для интерполяции определяется с учетом того, что i > g при K < 100.
Можно применить и метод приближенной оценки, согласно которому
 . (11.11)
. (11.11)
В этой формуле средний годовой доход от облигации соотносится со средней ее ценой. За простоту расчета, впрочем, приходится платить потерейточности оценки.
Пример 11.4. Облигация со сроком пять лет, проценты по которой выплачиваются один раз в году по норме 8%, куплена по курсу 97.
Текущая доходность по облигации 8 / 97 = 0,08247.
Для оценки полной доходности запишем исходное равенство (11.7):
0,97 = (1 + i)-5 + 0,08 a 5; i.
Для интерполяции примем следующие значения ставок: i' = 0,085, i" = 0,095. Согласно (11.7) находим
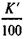 = 1,085-5 + 0,08 а 5;8,5 = 98,03;
= 1,085-5 + 0,08 а 5;8,5 = 98,03;
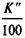 = 1,095-5 + 0,095 а 5;9,5 = 94,24.
= 1,095-5 + 0,095 а 5;9,5 = 94,24.
Отсюда
i = 8,5 + 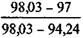 (9,5 - 8,5) = 8,77.
(9,5 - 8,5) = 8,77.
Для проверки рассчитаем курс для ставки помещения 8,77%. Получим
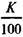 = 1,0877-5 + 0,08 а 5;8,77 = 96,99.
= 1,0877-5 + 0,08 а 5;8,77 = 96,99.
Как видим, расчетный курс весьма близок к рыночному — 97. Приближенное решение по (11.11) дает
i = 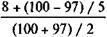 = 8,73,
= 8,73,
что соответствует рыночному курсу 97,2. Погрешность выше, чем при использовании линейной интерполяции.
Облигации с выкупной ценой, отличающейся от номинала. В этом случае проценты начисляются на сумму номинала, а прирост капитала равен С - Р, где С — выкупная цена. Соответственно при оценке ставки помещения необходимо внести соответствующие коррек-
тивы в приведенные выше формулы. Например, внесякоррективы в (11.6) и (11.7), получим
 (11.12)(11.13)
(11.12)(11.13)
а вместо (11.11)
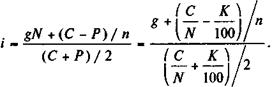 (11.14)
(11.14)
Пример 11.5. Сравним по доходности две облигации с ежегодными выплатами процентов (табл. 11.1). Параметры облигации A взяты из предыдущего примера.
Таблица 11.1
| Облигация | Номинал/ выкупная цена | Срок, лет | Купонный доход, % | Курс |
| А | 100 / 100 | |||
| В | 100 / 110 |
Показатели доходности для этих облигаций приведены в табл. 11.2.
Таблица 11.2
| Показатели доходности | |||
| Облигация | Купонная | Текущая | Полная |
| А | 8,25 | 8,77 (8,73) | |
| Б | 9,17 | 8,04 (8,12) |
Как видим, вотношении полной доходности преимущество на стороне облигации A, хотя текущая доходность у нее ниже, чём у второй. Приближенный метод расчета по (11.11) — соответствующиепоказателиприведеныв скобках — заметно завысил оценку показателя полной доходности у облигации Б.
Все рассмотренные выше формулы для расчета полной доходности предполагают, что оценка производится на начало срока облигации или на дату выплаты процентов. Для случая, когда оценка производится на момент между двумя датами выплат процентов, приведенные формулы дадут смещенные оценки.
Поиск по сайту: