Наращение по простой процентной ставке

Формула наращения. Под наращенной суммой (amount, maturity value) ссуды (долга, депозита, других видов выданных в долг или инвестированных денег) понимают первоначальную ее сумму с начисленными процентами к концу срока (date of maturity, due date). Наращенная сумма определяется умножением первоначальной суммы долга (principal) на множитель наращения, который показывает, во сколько раз наращенная сумма больше первоначальной. Расчетная формула зависит от вида применяемой процентной ставки и условий наращения.

Для записи формулы наращения простых процентов (simple interest) примем обозначения:

I — проценты за весь срок ссуды;

P — первоначальная сумма долга;

S — наращенная сумма, или сумма в конце срока;

i — ставка наращения (десятичная дробь);

n — срок ссуды.

Срок обычно измеряется в годах, соответственно i — годовая ставка. Каждый год приносит проценты в сумме Pi. Начисленные за весь срок проценты (accrued interest) составят I=Pni.

Наращенная сумма, таким образом, находится как

S = Р+ I = Р(1 + ni). (1.1)

Выражение (1.1) называют формулой наращения по простым процентам или кратко — формулой простых процентов, а множитель — множителем наращения простых процентов. График роста по простым процентам представлен на рис. 1.1.

Заметим, что увеличение процентной ставки или срока в k раз увеличит множитель наращения в (1 + kni) / (1 + ni) раз.

Пример 1.1. Определим проценты и сумму накопленного долга, если ссуда равна 700 тыс. руб., срок — четыре года, проценты простые, ставка — 20% годовых. Находим

I = 700 х 4 х 0,2 = 560 тыс. руб.; S = 700 + 560 = 1260 тыс. руб.

Увеличим ставку в два раза. Сумма процентов при этом удвоится, однако наращенная сумма увеличится в (1 + 2 х 4 х 0,2) / (1 + 4 х 0,2) = 1,444 раза.

Практика расчета процентов для краткосрочных ссуд. Обычно к наращению по простым процентам прибегают при выдаче краткосрочных ссуд (на срок до одного года) или в случаях, когда проценты не присоединяются к сумме долга, а периодически выплачиваются кредитору. Поскольку ставка, как правило, фиксируется в контракте в расчете за год, то при сроке ссуды менее года необходимо определить, какая часть годового процента уплачивается кредитору. Аналогичная проблема возникает и в других случаях, когда срок ссуды меньше периода начисления.

Рассмотрим наиболее распространенный в практике случай — с годовым периодом начисления. Для начала выразим общий срок п в виде дроби:

где t — число дней ссуды;

K — число дней в году, или временная база (time basis).

При расчете простых процентов предполагают, что K = 360 (12 месяцев по 30 дней) или K = 365, 366 дней. Если K = 360, то получают обыкновенные, или коммерческие, проценты (ordinary interest), a при использовании действительной продолжительности года (365, 366) получают точные проценты (exact interest).

Число дней ссуды также можно измерить приближенно и точно. В первом случае продолжительность ссуды определяется из условия, согласно которому любой месяц принимается равным 30 дням. Точное число дней ссуды определяется путем подсчета числа дней между датой выдачи ссуды и датой ее погашения. День выдачи и день погашения считаются за один день. Для подсчета числа дней можно воспользоваться табл. 1 Приложения.

Итак, возможны и применяются на практике три варианта расчета простых процентов:

а) точные проценты с точным числом дней ссуды. Этот вариант, естественно, дает самые точные результаты. Данный способ применяется центральными банками многих стран и крупными коммерческими банками, например в Великобритании. Обычно он обозначается как 365/365 или ACT/ACT;

б) обыкновенные проценты с точным числом дней ссуды. Этот метод, иногда называемый банковским (Banker's Rule), распространен в ссудных операциях коммерческих банков, в частности во Франции. Он обозначается как 365/360 или ACT/360. Этот вариант дает несколько больший результат, чем применение точных процентов. Заметим, что при числе дней ссуды, превышающем 360, данный способ приводит к тому, что сумма начисленных процентов будет больше, чем предусматривается годовой ставкой. Например, если t = 364, то n = 364/360 = 1,011;

в) обыкновенные проценты с приближенным числом дней с суд ы. Такой метод применяется тогда, когда не требуется большой точности, например при промежуточных расчетах. Он принят в практике коммерческих банков Германии. Этот метод обозначается как 360 / 360.

Вариант расчета с точными процентами и приближенным числом дней ссуды лишен смысла и не применяется.

Заметим, что поскольку точное число дней ссуды в большинстве случаев, но, разумеется, не всегда больше приближенного (в чем легко убедиться, определив среднее за год число дней в месяце, которое равно 30,58), то проценты с точным числом дней обычно дают больший рост.

Пример 1.2. Ссуда в размере 1 млн. руб. выдана 20 января до 5 октября включительно под 18% годовых. Какую сумму должен заплатить должник в конце срока? При решении применим все три метода. Предварительно определим число дней ссуды: точное — 258, приближенное — 255.

1. Точные проценты с точным числом дней ссуды (365 / 365):

руб.

2. Обыкновенные проценты с точным числом дней ссуды (360/365):

руб.

3. Обыкновенные проценты с приближенным числом дней ссуды (360/360):

руб.

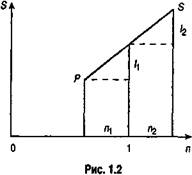
Начисление процентов в смежных календарных периодах. Выше при начислении процентов не принималось во внимание расположение срока ссудной операции относительно календарных периодов. Вместе с тем часто даты начала и окончания ссуды находятся в двух смежных календарных отрезках времени. Ясно, что начисленные проценты не могут быть целиком отнесены к одному из них. Необходимость деления общей суммы процентов между периодами возникает в бухгалтерском учете, при налогообложении, финансовом анализе деятельности предприятия. Алгоритм деления общей массы процентов очевиден (рис. 1.2). Если общий срок ссуды захватывает два смежных календарных периода, причем на первый период приходится срок n ₁, на второй — n ₂, то

Переменные ставки. В кредитных соглашениях иногда предусматриваются изменяющиеся во времени процентные ставки. Если это простые ставки, то наращенная на конец срока сумма определяется следующим образом:

(1.2)

где i_t - ставка простых процентов в периоде t, t = 1,2,..., m;

n_t — продолжительность периода;

Пример 1.3. Контракт предусматривает следующий порядок начисления процентов: первый год — ставка 16%, в каждом последующем полугодии ставка повышается на 1%. Необходимо определить множитель наращения за 2,5 года. Находим

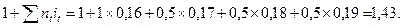
Многие коммерческие банки России практикуют начисление и выплату процентов вкладчика ежеквартально или ежемесячно, причем начисление производится по постоянной или изменяющейся (растущей) процентной ставке. Для этого в контракте фиксируется одна или ряд годовых ставок, исходя из которых определяются размеры квартальных или месячных ставок. Годовые ставки в этом случае назовем номинальными. Например, один из крупных коммерческих банков в 1994 г. привлекал средства населения, предлагая следующие переменные номинальные ставки для поквартального начисления и выплат процентов: 165, 195, 240, 295%. Таким образом, за первый квартал выплачивается 165 / 4 = 41,25%, за второй — 195 / 4 = 48,75% и т.д.

Реинвестирование. В практике при инвестировании средств в краткосрочные депозиты иногда прибегают к неоднократному последовательному повторению наращения по простым процентам в пределах заданного общего срока, т.е. к реинвестированию (rollover) полученных на каждом этапе наращения средств. Наращенная сумма для всего срока составит в этом случае

S = (1 + n ₁ i ₁)(l + n ₂ i ₂) (1.3)

где i_t — ставки, по которым производится реинвестирование.

Если периоды начисления и ставки не изменяются во времени, то вместо формулы (1.3) имеем:

S = P (1 + ni) ^m, (1.4)

где m — количество реинвестиций.

Пример 1.4. 100 тыс. руб. положены 1 марта на месячный депозит под 20% годовых. Какова наращенная сумма, если операция повторяется три раза? Если начислять точные проценты, то

тыс. руб.

Начисление обыкновенных процентов дает

тыс. руб.

Поиск по сайту: