Доходность купли-продажи финансовых инструментов

Краткосрочные финансовые инструменты денежно-кредитного рынка — векселя, тратты, различные депозитные сертификаты и т.д. — могут быть проданы до наступления срока их оплаты. Владелец при этом получает некоторый доход, а в неблагоприятных условиях несет убытки.

Покупка и продажа векселя (простая учетная ставка). Если вексель или другой вид долгового обязательства через некоторое время после его покупки и до наступления срока погашения продан, то эффективность этой операции можно измерить в виде простых или сложных процентов. Финансовая результативность операции здесь связана с разностью цен купли-продажи, которые в свою очередь определяются сроками этих актов до погашения векселя и уровнем учетных ставок. Покажем это. Пусть номинал векселяравен S руб. Он был куплен (учтен) по учетной ставке d ₁ за дней до наступления срока.

Цена в момент покупки составила

где K — временная база учета.

За дней до погашения вексель был продан с дисконтированием по ставке d ₂:

Инвестиции в начале операции составили, таким образом, P ₁ руб., отдача от них P ₂ руб. Операция продолжалась дней. Наращение вложений за указанный срок по простой или сложной годовой ставке, которую принимают в качестве меры эффективности, должно дать конечный результат, т.е. P ₂. Условия операции показаны на рис. 9.4. Для простой ставки i_ЭП получим следующее балансовое уравнение:

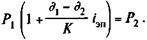(9.7)

Отсюда доходность купли-продажи векселя (в виде ставки простых процентов)

(9.8)

Выразив p ₁ и P ₂ через определяющие эти величины параметры, находим

(9.9)

Для того чтобы операция не была убыточной, необходимо, чтобы

или P ₁ < P ₂.

Аналогично поступают и при использовании в качестве меры эффективности годовой сложной ставки. В этом случае, полагая K = 365, на основе балансового уравнения

(9.10)

получим

(9.11)

Заметим, что уравнения (9.10) и сходное по содержанию (9.7) пригодны для оценки i_Э или i_ЭП в ситуациях, когда речь идет о купле-продаже финансового инструмента (приносящего доход в любой форме) и известны цены и длительность владения (holding period).

Заменив в формуле (9. 11) P ₂ и P ₁ на адекватные выражения, находим

(9.12)

Очевидно, что реальная доходность (т.е. когда i_Э > 1), как и в случае с простыми процентами, будет иметь место, если или P ₁ < P ₂. В противном случае операция приносит убыток. Нетрудно догадаться, что операция будет доходной до тех пор, пока

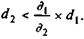
Пример 9.5. Вексель куплен за 167 дней до его погашения, учетная ставка — 6%. Через 40 дней его реализовали по учетной ставке 5,75%. Эффективность, выраженная в виде простой годовой ставки процентов (временная база учета K = 360, наращения K = 365), составит согласно (9.9):

i_ЭП = 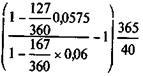= 0,0708.

Эффективность операции, измеренная в виде эквивалентной ставки сложныхпроцентов, равна:

i_Э = = 0,0731.

Эту же величину получим и непосредственно по формуле (9.12):

i_Э = = 0,0731.

Продолжим пример. Определим допустимый предел для учетной ставки, применимой при продаже векселя(d ₂). Находим, что для того, чтобы операция купли-продажи векселя принесла некоторый доход, учетная ставка d ₂ должна быть меньше, чем

х 0,06 = 0,0788976.

Покупка и продажа финансового инструмента, приносящие простые проценты. Если депозитный сертификат или другой подобного рода краткосрочный инструмент через некоторое время после его покупки и до наступления срока погашения вновь продан, то эффективность (доходность) такой операции можно измерить в виде ставки простых или сложных процентов. Финансовая эффективность такой операции зависит от сроков актов купли-продажи до погашения инструмента, цен или процентных ставок, существующих на денежном рынке в моменты покупки и продажи.

Несколько слов о депозитных сертификатах. Они, как известно, выпускаются банками как кратко-, так и среднесрочные финансовые инструменты; продаются эмитентом в момент выпуска по номиналу (at par) и предусматривают в качестве дохода выплату процентов, начисляемых по простым или сложным ставкам. Проценты чаще всего выплачиваются один раз в конце срока. В случае досрочной продажи сертификата эмитенту иногда предусматриваются штрафные санкции. Например, удержание процентов за один - три месяца. Сертификаты являются объектом инвестиций и обычно могут быть проданы на рынке ценных бумаг.

Сертификат обеспечивает владельцу доходность на уровне объявленной процентной ставки в том случае, когда сертификат находится у владельца полный срок. Иное дело, если этот финансовый инструмент продается на рынке ценных бумаг по рыночной цене.

Обратимся к наиболее распространенному виду сертификата — с разовой выплатой процентов — и рассмотрим три возможных варианта операции купли-продажи этого инструмента по срокам:

а) покупается по номиналу, продается за дней до погашения;

б) покупается после выпуска и погашается в конце срока;

в) покупается и продается в пределах объявленного срока.

Для варианта а получим знакомое равенство (9.7):

,

однако символы здесь имеют другое содержание, а именно: Р ₁ - номинал, P ₂ — цена продажи, — сроки до погашения.

Доходность владения сертификатом в течение дней определяется формулой (9.8), если расчет исходит из цен сертификата. Если же в качестве исходных параметров берутся процентные ставки i ₁ и i ₂ (i ₁ — объявленная ставка сертификата, i ₂ — ставка рынка в момент продажи), то

(9.13)

В случае когда измерителем эффективности выступает сложная процентная ставка и заданы цены, получим формулу, аналогичную (9.11). Если расчет основан на уровнях процентных ставок, то

(9.14)

Отметим, что доходность операции имеет место только в том случае, когда Предельное значение i, при котором инвестор получит доход, равно

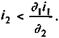
Перейдем теперь к варианту б. Здесь справедливо равенство

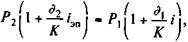
где P ₁ - номинал;

P ₂ -цена приобретения;

i -объявленная процентная ставка.

Контур для данного уравнения приведен на рис. 9.4. Из приведенного равенства получим значение i _ЭП при заданной величине P ₂:

(9.15)

Если в качестве измерителя эффективности принята ставка сложных процентов, то

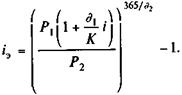(9.16)

Рассмотрим вариант в. Здесь покупка производится спустя некоторое время после выпуска сертификата, а его продажа — до момента погашения. В этом случае опять приходим к уравнению (9.7), в котором P ₁ означает цену приобретения (а не номинал). Отсюда для расчета i_ЭП и i_Э пригодны формулы (9.8) — (9.11).

Как видим, на величины i_ЭП и i_Э в вариантах а, в влияют как срок владения инструментом, так и колебания процентных ставок.

Пример 9.6. Операция заключается в покупке сертификата за 1020 тыс. руб. за 160 дней до его выкупа. Инструмент был продан за 1060 тыс. руб. через 90 дней. Какова доходность операции, измеренная в виде простой и сложной ставок? Исходные данные: Р ₁ = 1020, P ₂ = 1060, = 160, = 70, = 90.

Пусть временная база простых процентов равна 365 дням, тогда по формуле (9.8) находим

i_ЭП = 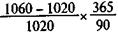= 0,159, т.е. 15,9%. Эквивалентная сложная ставка равна

i_Э = = 0,169, т. е. 16,9%.

Величину i_Э можно определить и непосредственно по формуле (9.11):

i_Э = = 0,169.

Пример 9.7. Финансовый инструмент, приносящий постоянный процент, куплен за 200 дней до срока его погашения и продан через 100 дней. В момент покупки процентная ставка на рынке была равна 10%, в момент продажи — 9,8%. Доходность операции купли-продажи в виде годовой ставки сложных процентов равна согласно (9.14)

i_Э = = 0,103, т.е. 10,3%.

Пример 9.8. Сертификат с номиналом 100 тыс. руб. с объявленной доходностью 12% годовых (простые проценты) сроком 720 дней куплен за 110 тыс. руб. за 240 дней до его оплаты. Какова доходность инвестиций в виде i_Э?

Если K = 360 дней, то по формуле (9.16) получим

i_Э = = 0,19985, т. е. 19,985%.

Поиск по сайту: