 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Погашение задолженности частями
Контур финансовой операции. Необходимым условием финансовой или кредитной операции в любой ее форме является сбалансированность вложений и отдачи. Понятие сбалансированности удобно пояснить на графике. Пусть ссуда в размере D 0выдана на срок Т. На протяжении этого срока в счет погашения задолженности производятся, допустим, два платежа: R 1, и R 2, а в конце срока выплачивается остаток задолженности (balance) в сумме R 3(рис 1.3а) (для нас здесь не имеет значения, какая часть этой суммы идет на выплату процентов, а какая на погашение долга). Очевидно, что на интервале t 1задолженность возрастает (в силу начисления процентов) до величины D 1,. В конце этого периода в счет погашения задолженности выплачивается сумма R 1, долг уменьшается до K 1и т.д. Заканчивается операция получением кредитором в окончательный расчет суммы R 3. В этот момент задолженность должна быть равна нулю. Назовем такой график контуром операции (рис. 1.3б).
Сбалансированная операция обязательно имеет замкнутый контур, иначе говоря, последняя выплата полностью покрывает остаток задолженности. В этом случае совокупность платежей точно соответствует условиям сделки. Контур операции мы будем неоднократно применять в книге при обсуждении ряда финансовых операций, в частности при погашении задолженности частичными (промежуточными) платежами.
Частичные платежи. Краткосрочные обязательства иногда погашаются с помощью последовательности частичных платежей. В этом случае надо решить вопрос о том, какую сумму надо брать за базу для расчета процентов и каким путем определять остаток задолженности. Существуют два метода решения этой задачи. Первый метод, который применяется в основном в операциях со сроком более года, называют актуарным (Actuarial Method). Второй метод назван правилом торговца (Merchant's Rule). Он обычно применяется коммерческими фирмами в сделках со сроком не более года.
Если иное не оговорено, то, как правило, при начислении процентов используются обыкновенные проценты с приближенным числом дней.
Актуарный метод предполагает последовательное начисление процентов на фактические суммы долга. Частичный платеж идет в первую очередь на погашение процентов, начисленных на дату платежа. Если величина платежа превышает сумму начисленных процентов, то разница идет на погашение основной суммы долга. Непогашенный остаток долга служит базой для начисления процентов за следующий период и т.д. Если же частичный платеж меньше начисленных процентов, то никакие зачеты в сумме долга не делаются. Такое поступление приплюсовывается к следующему платежу. Для случая, показанного на рис. 1.3, получим следующие расчетные формулы для определения остатка задолженности:
K 1 = D 0(1 + t 1 i) - R 1; K 2 = K 1(1 + t 2 i) - R 2; K 2(l + t 3 i) - R 3 = 0.

Пример 1.5. Имеется обязательство погасить за 1,5 года (с 12 марта 1994 г. по 12 сентября 1995 г.) долг в сумме 15 млн. руб. Кредитор согласен получать частичные платежи. Проценты начисляются по ставке 20% годовых. Частичные поступления характеризуются следующими данными (в тыс. руб.):
| 12 июня 1994 г. — 500; | ||
| 12 июня 1995 г. — 5000; | ||
| 30 июня 1995 г. — 8000; | ||
| 12 сентября 1995 г. —? |
Решение представим в последовательной записи:
| 12 марта 1994 г. | долг | 
|
| 12 июня 1994 г. | долг с процентами | |
| Поступление | -500 |
Поскольку поступившая сумма меньше начисленных процентов (750), то она присоединяется к следующему платежу.
| 12 июня 1995 г. | Долг с процентами | |
| Поступления | 500 + 5000 | 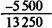
|
| Остаток долга | ||
| 30 июня 1995 г. | Долг с процентами | 13382,5 |
| Поступление | 
| |
| Остаток долга | ||
| 12 сентября 1995 г. | Долг с процентами | 5594,5 |
Контур данной операции представлен на рис. 1.4.
Нетрудно понять, что актуарный метод в известной мере нарушает принцип начисления простых процентов, так как проценты начисляются не на первоначальную сумму долга, а на остаток задолженности, который в ряде случаев может частично содержать ранее начисленные проценты. Такая ситуация, разумеется, не возникает тогда, когда на каждом этапе выплачиваются только проценты.

Рис. 1.4

Иной подход предусматривается правилом торговца. Здесь возможны два варианта.
Если срок ссуды не превышает год, то сумма долга с начисленными за весь срок процентами остается неизменной до полного погашения. Параллельно идет накопление частичных платежей с начисленными на них до конца срока процентами. Последний взнос должен сбалансировать долг и платежи.
В случае когда срок превышает год, указанные выше расчеты делаются для годового периода задолженности. В конце года из суммы задолженности вычитается наращенная сумма накопленных частичных платежей. Остаток погашается в следующем году. Алгоритм можно записать следующим образом:
 (1.5)
(1.5)
где S — остаток долга на конец срока или года;
D — наращенная сумма долга;
K — наращенная сумма платежей;
rj — сумма частичного платежа;
п — общий срок ссуды;
tj — интервал времени от момента платежа до конца срока ссуды или года.
Графическое изображение такой операции охватывает два как бы параллельных контура (рис. 1.5). Второй относится к промежуточному платежу.
Заметим, что для одних и тех же данных актуарный метод и правило торговца в общем случае дают разные результаты. Результат первого метода немного выше, чем второго.
Пример 1.6. Обязательство, датированное 10 августа 1994 г., должно быть погашено 10 июня 1995 г. Ссуда (1,5 млн. руб.) выдана под 20% годовых. В счет погашения долга 10 декабря 1994 г. поступило 800 тыс. руб. Остаток долга на конец срока согласно формуле (1.5)
 млн. руб.
млн. руб.
При применении актуарного метода получим
 млн. руб.
млн. руб.
Поиск по сайту: