Наращение процентов, налоги и инфляция (простые и сложные проценты)

В рассмотренных выше методах определения наращенной суммы не учитывались такие важные моменты, как налоги и инфляция.

Налог на полученные проценты. В ряде стран полученные (юридическими, а иногда и физическими лицами) проценты облагаются налогом, что, естественно, уменьшает реальную наращенную сумму. Нельзя не учитывать и то, что частый пересмотр налоговых правил вносит существенный элемент неопределенности в конечные результаты наращения для владельца денег[3].

Обозначим, как и выше, наращенную сумму до выплаты налогов (tax-free) через S,а с учетом выплаты как S". Пусть ставка налога на проценты равна g.

При начислении простых процентов находим:

S" = S - (S - P) g - S (1 - g) + Pg = P [1+ n (1 - g)i ].

Таким образом, учет налога сводится к соответствующему сокращению процентной ставки: вместо ставки i фактически применяется ставка (1 - g) i.

В долгосрочных операциях при начислении налога на сложные проценты возможны следующие варианты: налог начисляется за весь срок сразу, т.е. на всю сумму процентов, или последовательно, например в конце каждого года. В первом случае сумма налога равна P [(1 + i) ⁿ - 1] g, а наращенная сумма после выплаты налога

S" = S - (S - P) g = S (1 - g)+ Pg = P [(1 - g)(1+ i) ⁿ + g ].(2.38)

Во втором случае сумма налога определяется за каждый истекший год. Очевидно, что она является переменной величиной, так как сумма процентов увеличивается во времени. Соответственно увеличивается и годовая сумма налогов. Сумма налогов за весь срок, очевидно, не зависит от метода начисления.

Налог за год t (обозначим его как G_t)можно найти с помощью следующего рекуррентного выражения:

G_t = I_tg = (S_t - S_{t- 1}) g = P [(1 + i) ^t - (1 + i) ^{t -1}] g. (2.39)

Пример 2.21. Пусть ставка налога на проценты равна 10%. Процентная ставка — 30% годовых, срок начисления — три года. Первоначальная сумма ссуды — 1000 тыс. руб. Определим наращенную сумму с учетом выплаты налога на проценты.

При начислении простых процентов за весь срок получим: наращенная сумма без уплаты налога S = 1900 тыс. руб., с учетом его выплаты в конце срока S" = 1000(1 + 3 х 0,9 х 0,3) = 1810 тыс. руб., сумма налога 90 тыс. руб.

Начислим теперь сложные проценты. Наращенная сумма без уплаты налога S = 2197 тыс.руб., с учетом его выплаты S'' = 1000[(1 - 0,1)(1 + 0,3)³ + 0,1] = 2077,3 тыс.руб.

Сумма налога равна 119,7 тыс. руб., причем согласно формуле (2.39) за первый год выплачивается 1000(1,3¹ - 1,3⁰)0,1 = 30 тыс. руб., за второй год — 1000(1,3² - 1,3)0,1 = 39 тыс. руб., за третий год - 1000(1,3³ - 1,3²)0,1 = 50,7 тыс. руб.

Инфляция. В рассмотренных выше методах наращения все денежные величины измерялись по номиналу. Иначе говоря, не принималось во внимание снижение реальной покупательной способности денег за период, охватываемый финансовой операцией. Однако в современных, особенно российских, условиях инфляция часто играет решающую роль и без ее учета конечные результаты представляют собой весьма и весьма условную величину.

Инфляцию необходимо учитывать по крайней мере в двух случаях: при расчете наращенной суммы денег и при измерении реальной эффективности (доходности) финансовой операции. Остановимся на этих проблемах.

Прежде всего напомним, что изменение покупательной способности денег за некоторый период измеряется с помощью соответствующего индекса J_nc. Пусть S — наращенная сумма денег, измеренная по номиналу. Эта же сумма, но с учетом ее обесценения составит:

C = S х J_nc.

Индекс покупательной способности денег, как известно, равен обратной величине индекса цен:

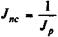
Разумеется, указанные индексы должны относиться к одним и тем же временным интервалам. Пусть, например, сегодня получено 150 тыс. руб., известно, что за два предшествующих года цены увеличились в три раза, т.е. J_p = 3. В этом случае индекс покупательной способности денег равен 1/3. Следовательно, реальная покупательная способность 150 тыс. руб. составит в момент получения всего 150 х (1/3) = 50 тыс. руб. в деньгах двухлетней давности.

Нетрудно связать индекс цен и темп инфляции. Предварительно напомним некоторые понятия. Под темпом инфляции обычно понимается относительный прирост цен за период; обозначим его как H; измеряется он в процентах. Темп инфляции и индекс цен связаны следующим образом:

Н = 100(J_p - 1).

В свою очередь

Например, если темп инфляции равен 130%, то цены за этот период выросли в 2,3 раза.

Среднегодовые темп роста цен (i_p) и темп инфляции (h) находятся на основе величины J_p как:

Поскольку инфляция является цепным процессом (цены в текущем периоде повышаются на h_t процентов относительно уровня, сложившегося в предыдущем периоде), то индекс цен за несколько таких периодов равен произведению цепных индексов цен:

(2.40)

Пусть теперь речь идет о будущем. Если h — постоянный ожидаемый (или прогнозируемый) темп инфляции за период, то за n таких периодов получим

(2.41)

Грубой ошибкой, которая, к сожалению, встречается в российской практике (даже в экономических публикациях, претендующих на научность!), является суммирование темпов инфляции для получения обобщающего показателя инфляции за период. Это, кстати, заметно снижает величину получаемого показателя.

Поиск по сайту: