 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Нестандартные ипотеки
|
Читайте также: |
Ипотека с ростом платежей (GRM). Общая схематакой ссуды в основном не отличается от стандартной. Различие лишь в том, что первый взнос минимален, затем на некотором начальном интервале времени (пять - десять лет) они увеличиваются с постоянным темпом, далее они постоянны. Как уже отмечено выше, в первые годы текущие расходы должника могут оказаться меньше, чем суммы начисленных процентов. В этом случае основная сумма долга некоторое время будет увеличиваться — см. рис. 8.2.

Разделим весь срок погашения ссуды на два интервала протяженностью т и М месяцев. В первом периоде расходы растут с постоянным темпом роста g.
Rt = R 1 gt- 1,
где R 1 - расходыв первом месяце;
g - ежемесячный темп роста расходов.
Во втором периоде расходы должника равны постоянной величине
R = R1gm- 1. (8. 6)
Найдем современную стоимость платежей каждого периода относительно начала действия контракта. Поскольку в первом периоде последовательность платежей представляет собой геометрическую прогрессию, то искомая величина находится(см. формулу 5.14) как
 (8.7)
(8.7)
Во втором периоде платежи представляют собой отложенную постоянную ренту с членом R. На начало действия контракта современная стоимость этой ренты определяется как
A 2 = RaM;iv m = R 1 gm- 1 aM;iv m. (8.8)
Приравняем современную стоимость всего потока платежей к сумме задолженности, после чего, использовав формулы (8.6) - (8.8) и выполнив ряд преобразований, находим:
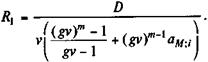 (8.9)
(8.9)
Пример 8.3. Сумма задолженности по договору ипотеки — 100 млн. руб., общий срок погашения — 20 лет (240 месяцев); предусматривается рост платежей в течение 60 месяцев; процентная ставка за ссуду — 10% годовых; ежегодный прирост платежей — 5%. Необходимо разработать график погашения.
Исходные данные: m = 60, M = 180, i = 0,1 / 12 = 0,08333, v = 0,991735, ежемесячный темп роста расходов в первом периоде составит: g =  = 1,004074.
= 1,004074.
На основе приведенных данных по формуле (8.9) находим:
R = 802,87 тыс. руб.
Таким образом, ежемесячные расходы в первом периоде определяются как 802,87 х 1,004074 t - 1. Например, расходы в конце пятилетнего периода равны:
R = 802,87 х 1,00407460 - 1 = 1020,52 тыс. руб.
Эта же сумма ежемесячно выплачивается во втором периоде (см. табл. 8.2).
Таблица 8.2
| Месяц | Остаток долга на начало месяца | Взнос | Проценты | Погашение долга |
| 100000,00 | 802,87 | 833,33 | - 30,46 | |
| 100030,46 | 806,14 | 833,58 | - 27,44 | |
| 100057,90 | 809,43 | 833,81 | - 24,38 | |
| ... | ||||
| 100 162,25 | 832,79 | 834,68 | -1,89 | |
| 100164,14 | 836,19 | 834,70 | 1,49 | |
| 100157,75 | 839,59 | 834,64 | 4,94 | |
| ... |
Таблица 8.2 (продолжение)
| Месяц | Остаток долга на начало месяца | Взнос | Проценты | Погашение долга |
| 95416,91 | 1 016,38 | 795,14 | 221,24 | |
| 95195,67 | 1 020,52 | 793,29 | 227,22 | |
| 94968,45 | 1 020,52 | 791,40 | 229,12 | |
| ... | ||||
| 2015,72 | 1 020,52 | 16,84 | 1003,68 | |
| 1 012,04 | 1 020,52 | 8,48 | 1012,04 |
Как видим, сумма начисленных процентов в первом периоде меньше взноса. Адекватно увеличивается сумма долга. Максимальная сумма долга приходится на начало одиннадцатого месяца. Начиная с одиннадцатого месяца взносы превышают сумму процентов.
Ссуда с периодическим увеличением взносов. В этом варианте ипотеки задается последовательность размеров взносов. Пусть увеличение взносов происходит через равные интервалы времени т. Очевидно, что для полной сбалансированности схемы размер последнего взноса не задается, он определяетсяпо сумме остатка задолженности.
Обозначим размеры взносовкак R 1,..., Rk. Определим размер последнего взноса. Для этого найдем сумму современных стоимостей взносов от первого до k - 1 на начало операции. Обозначим ее как Q.

Современная стоимость непокрытой взносами задолженности
W = D - Q.
Отсюда размер взносов в последнем периоде
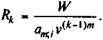
Ссуда с льготным периодом. На этом видеипотеки, вероятно, нет нужды останавливаться подробно. В льготном периоде здесь выплачиваются только проценты, поэтому основная сумма долга не изменяется. Расчет размеров взносов осуществляется так же, как и для стандартной ипотеки.

Ссуда с залоговым счетом. Как уже отмечалось выше, для должника в отношении метода погашения эта ипотека обычно не отличается от ипотечной схемы GPM. Для кредитора это стандартная ипотека. Такое совмещение двух схем достигается открытием специального залогового счета, на который должник (или третья сторона) вносит оговоренную сумму. С этого счета в погашение долга списываются некоторые суммы. Недостающие средства доплачиваются должником. Этим достигаются некоторое обеспечение выплат и сокращение расходов должника в первые т месяцев. Схема такой ипотеки представлена на рис. 8.3 (данные взяты из примера 8.4).
В зависимости от того, какая величина задается, возможны различные постановки задачи. Рассмотрим одну из них — пусть заданным является размер залогового счета и необходимо определить суммы взносов с учетом частичного погашения путем списания с этого счета. Решение охватывает три этапа. На первом по формуле (8.1) рассчитывается необходимый размер взносов R, далее определяются суммы списания с залогового счета в первые m месяцев, на последнем этапе находятся суммы доплат до требуемого размера взносов R.
Для определения сумм списания примем обозначения:
Vt — сумма, списываемая с залогового счета;
r — месячная ставка процента, начисляемого на средства залогового счета;
Z — сумма залогового счета.
Обычно суммы списания со счета сокращаются во временис постоянным темпом, таким образом, соответственно размеры доплат увеличиваются. Находим
Vt = Vt - 1 q = V 1 qt - 1
где q — годовой темп изменения сумм, списываемых с залогового счета.
Суммы списаний представляют собой переменную ренту, современная стоимость которой равна первоначальной сумме залогового счета. Согласно формуле (5.15)
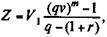
где V — дисконтный множитель по ставке r.
Отсюда
 (8.10)
(8.10)
В итоге
Rt = R - Vt; t = 1,..., т. (8.11)
Пример 8.4. Стоимость закладываемого имущества — 120 млн. руб. Продавец получает засчет ссуды 115 и от покупателя 5 млн. руб. Срок ипотеки — 10 лет. Покупатель открывает специальный счет (15 млн. руб.). На счет начисляются проценты по ставке 10% годовых номинальных(начисление помесячное), списание производится 20 месяцев, сумма списания уменьшается на 2% в месяц. Таким образом, Z = 15, т = 20, N = 120, q = 1,02, i = 12%, r = 10% (обе ставки годовые, номинальные). Находим
R = 115000 /a 120;1 = 1649,92 тыс. руб.;
Vi = 15000  = 978,15 тыс. руб.;
= 978,15 тыс. руб.;
Vt = 978,15 х 0,98 t - 1
Таким образом, суммы списания со счета равны: 978,15; 958,59;...; 653,33, а взносыдолжника в этом периоде 671,77; 691,33;...; 996,59.
Поиск по сайту: