Взаимоувязанные, последовательные потоки платежей

Долгосрочные финансовые операции часто предполагают наличие двух последовательных потоков платежей. Первый характеризует вложения (затраты), второй — отдачу от них (доходы). В самом

простом варианте — это покупка в рассрочку отложенной ренты. Напервом этапе идет накопление денежных средств, подпитываемое последовательными взносами, на втором — их расходование. Более сложным является инвестирование в создание производственного объекта. Второй денежный поток может следовать сразу после первого или несколько отставать от него. Иногда встречаются и более сложные схемы, когда указанные потоки платежей в некоторой части протекают одновременно.

При решении некоторых финансовых задач оба потока должны быть сбалансированы. Более подробно эта проблема применительно к оценке производственных инвестиций рассматривается в гл. 12. Здесь же остановимся на проблеме сбалансированности потоков в общем виде.

Очевидно, что баланс двух последовательных потоков имеет место при равенстве их современных стоимостей. Введем следующие обозначения: n — продолжительность периода вложений; t — срок, после которого начинается отдача; N — продолжительность потока доходов; m — продолжительность интервала между двумя потоками; K — величина члена первого потока; R — размер дохода;

A ₁ — современная стоимость потока вложений; _tА ₂ — современная стоимость потока доходов. Схематично условия задачи представлены на рис. 4.5. Очевидно, что t ≥ n, m ≥ 0.

Рассмотрим одну из возможных постановок задачи, когда в качестве заданных принимают параметры потока доходов, а параметры инвестиционного потока определяются в ходерасчета. Исходное равенство имеет вид:

A ₁ = _tA ₂

Для иллюстрации метода ограничимся самой простой задачей. Допустим, что речь идет об обеспечении поступлений регулярного дохода. Доходы и взносы постоянные, постнумерандо. В этом случае запишем равенство

Ka_n;i = Ra_N;iv^t.

Далее рассчитывается K или n.

Заметим, что v^t = vⁿv^m, отсюда следует, что с увеличением m уменьшается необходимая для выплаты будущих доходоввеличина K.

Пример 4.21. Необходимо обеспечить годовую ренту постнумерандо, выплачиваемую сразу после окончания срока взносов. Рента имеет параметры: R ₂ = 1, N = 10, i = 10%. Допустим, предполагается вносить по 1,2 млн. руб. в течение четырех лет. Проверим, достаточен ли такой срок.

Современная стоимость второй ренты A ₂ = 1 х a _10;10 x v ⁴ = = 4,19682. В свою очередь, приняв A ₁ = A ₂, получим A ₁ /R ₁ = = 3,49735. Прибегнув к формуле (4.27), находим

Иначе говоря, установленный срок взносов недостаточен. Корректировку условий можно осуществить, повысив размер взносов. Находим для четырех лет взносов

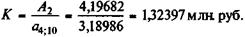
Если второй поток представляет собой p -срочную ренту, то

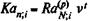
Практические приложения метода более подробно обсуждаются в параграфе 6.5 "Сберегательное (трастовое) обеспечение пенсий" и в гл. 12, посвященнойинвестициям.

Поиск по сайту: