Эквивалентность процентных ставок

Понятие эквивалентности использовалось выше применительно к платежам. Теперь распространим его на процентные ставки. Как было показано ранее, для процедур наращения и дисконтирования могут применяться различные виды процентных ставок. Определим теперь те их значения, которые в конкретных условиях приводят к одинаковым финансовым результатам. Иначе говоря, замена одного вида ставки на другой при соблюдении принципа эквивалентности не изменяет отношения сторон в рамках одной операции. Для участвующих в сделке сторон в общем безразлично, какой вид ставки фигурирует в контракте. Такие ставки назовем эквивалентными.

Проблема эквивалентности ставок уже затрагивалась в гл. 2 при определении эффективной ставки процента. Там было показано, что годовая эффективная ставка i эквивалентна номинальной ставке j при начислении процентов т раз в году. Рассмотрим теперь проблему эквивалентности ставок более полно и систематизировано. Сперва соотношения эквивалентности простых ставок, затем простых и сложных, далее эквивалентность различного вида сложных ставок, наконец, некоторые соотношения эквивалентности дискретных и непрерывных ставок.

Формулы эквивалентности ставок во всех случаях получим исходя из равенства взятых попарно множителей наращения. Приведем лишь один пример. Определим соотношение эквивалентности между простой и сложной ставками наращения. Для этого приравняем друг к другу соответствующие множители наращения:

(1 + ni_s) = (1 + i) ⁿ,

где i_s и i — ставки простых и сложных процентов.

Приведенное равенство предполагает, что начальные и наращенные суммы при применении двух видов ставок идентичны (рис. 3.4). Решение дает следующие отношения эквивалентности ставок:

(3.9) (3.10)

Аналогичным образом определим и другие, приведенные ниже соотношения эквивалентности ставок.

Эквивалентность простых процентных ставок. При выводе искомых соотношений между ставкой наращения и учетной ставкой следует иметь в виду, что при их применении используются временные базы K = 360 или K = 365 дней. Если временные базы одинаковы, то из равенства соответствующих множителей наращения следует:

(3.11) (3.12)

где: п — срок в годах;

i_s — ставка наращения;

d — учетная ставка.

Пример 3.12. Вексель учтен за год до даты его погашения по учетной ставке 15%. Какова доходность учетной операции в виде процентой ставки? По формуле (3.11) находим:

i_s = = 0,17647, или 17,647%.

Иначе говоря, операция учета по учетной ставке 15% за год дает тот же доход, что и наращение по ставке 17,647%.

Из приведенных формул и примера следует, что для одинаковых условий операции справедливо неравенство d < i_s. Следует обратить внимание и на то, что отношения эквивалентности между просты-

ми ставками существенно зависят от срока операции. С увеличением срока различия в размерах ставок становятся все более заметными. Например, для d = 10% находим

Пусть срок ссуды измеряется в днях, тогда, подставив в формулы (3.11) и (3.12) n = t/K, находим следующие соотношения эквивалентности:

а) временные базы одинаковы и равны 360 дням:

(3.13) (3.14)

б) если при начислении процентов принята база K = 365, а для учетной ставки K = 360, то

(3.15) (3.16)

Пример 3.13. Необходимо найти величину учетной ставки, эквивалентной годовой процентной ставке 80% (K = 365) при условии, что срок учета равен 255 дням. Находим по формуле (3.16)

d = = 0,50615, или 50,615%.

Эквивалентность простых и сложных ставок. Рассмотрим соотношения эквивалентности простых ставок i_s и d,с одной стороны, и сложных ставок i и j — с другой. Сложную учетную ставку здесь не будем принимать во внимание. Попарно приравняв соответствующие множители наращения, получим набор искомых соотношений.

Эквивалентность i_s и i (см. формулы (3.9) и (3.10)).

Эквивалентность i_s и j:

(3.17) (3.18)

Эквивалентность d и i:

(3.19) (3.20)

Эквивалентность d и j:

(3.21) (3.22)

Пример 3.14. Какой сложной годовой ставкой можно заменить в контракте простую ставку 18% (K = 365), не изменяя финансовых последствий для участвующих сторон? Срок операции 580 дней.

По формуле (3.10) находим эквивалентную сложную ставку:

= 0,17153, или17,153%

Эквивалентность сложных ставок. Рассмотрим наиболее важные соотношения эквивалентности для ставок i, j и d_c (напомним, d_c — сложная учетная ставка):

i = (1 + j/m)^m - 1; (3.23) (3.24)

(3.25) (3.26)

где d_c — сложная учетная ставка.

Приведем еще несколько полезных соотношений, которые нетрудно получить на основе формул (3.25) и (3.26). Напомним, что v = (1 + i)^-1:

d_c = iv, v = 1 - d_c, i - d_c = id_c. (3.27) (3.28) (3.29)

Заметим, что в зависимостях (3.23) — (3.29) срок не играет никакой роли.

Пример 3.15. При разработке условий контракта стороны договорились о том, что доходность кредита должна составлять 24% годовых. Каков должен быть размер номинальной ставки при начислении процентов ежемесячно, поквартально?

Эквивалентность сложных дискретных и непрерывных ставок. Теоретически можно найти соотношение эквивалентности между силой роста и любой дискретной процентной ставкой. Однако в этом, вероятно, нет необходимости. Ограничимся несколькими такими соотношениями, необходимость в которых может возникнуть в практических расчетах.

Эквивалентность и i. Из равенства следует:

(3.30) (3.31)

Эквивалентность и j:

(3.32) (3.33)

Эквивалентность 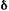и d_c. Из равенства 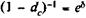следует:

(3.34) (3.35)

Приведем еще одно полезное соотношение:

Пример 3.16. Какая непрерывная ставка заменит поквартальное начисление процентов по номинальной ставке 20%? Согласно формуле (3.33) находим

= 4 х ln(1 + 0,2) = 0,19516, или 19,516%.

Формулы эквивалентности дискретных и непрерывных ставок позволяют расширить область применения непрерывных процентов. Как уже говорилось выше, непрерывные проценты во многих сложных расчетах дают возможность существенно упростить выкладки. Вместе с тем такие ставки непривычны для практика, поэтому после использования в расчетах формул непрерывных процентов нетрудно с помощью формул эквивалентности представить полученные результаты в виде общепринятых дискретных характеристик.

Поиск по сайту: