Конверсия валюты и наращение процентов

Рассмотренные выше методы наращения процентов позволяют перейти к обсуждению более сложных и важных в практическом отношении задач. Остановимся на одной из них. Речь пойдет о совмещении конверсии (обмена) валюты и наращении простых процентов.

При возможности обмена рублевых средств на СКВ и наоборот целесообразно сравнить результаты от непосредственного размещения имеющихся денежных средств в депозиты или опосредованно через другую валюту. Таким образом, имеются четыре варианта для наращения процентов:

без конверсии: СКВ→СКВ;

с конверсией: СКВ→Руб.→Руб.→СКВ;

без конверсии: Руб.→Руб.;

с конверсией: Руб.→СКВ→СКВ→Руб.

Варианты с конверсией показаны на рис. 1.8.

В операции наращения с конверсией валют существует два источника дохода: изменение курса и наращение процента, причем

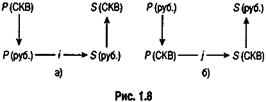
если второй из них безусловный (ставка процента фиксирована), то этого нельзя сказать о первом. Более того, двойное конвертирование валюты может быть и убыточным.

Вариант СКВ→Руб.→Руб.→СКВ. Проанализируем сперва вариант "а", показанный на рис. 1.8. Для записи формул примем следующие обозначения:

P_v — сумма депозита в СКВ;

Р_r — сумма депозита в рублях;

S_v — наращенная сумма в СКВ;

S_r — наращенная сумма в рублях;

k ₀ — курс обмена в начале операции (курс СКВ в руб.);

К ₁ — курс обмена в конце операции;

п — срок депозита;

i — ставка наращения для рублевых сумм;

j — ставка наращения для конкретного вида СКВ.

Операция предполагает три шага: обмен валюты на рубли, наращение процентов на эту сумму и, наконец, конвертирование в исходную валюту. Конечная (наращенная) сумма в валюте определяется как

(1.16)

Три сомножителя этой формулы соответствуют упомянутым трем шагам. Множитель наращения с учетом двойного конвертирования рассчитывается как

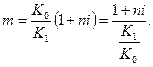(1.17)

Взаимодействие двух факторов роста исходной суммы здесь представлено наиболее наглядно. С ростом ставки множитель линейно увеличивается (прирост на единицу i равен [ K ₀/ K ₁] n),в свою очередь рост конечного курса уменьшает его — производная множителя по этому курсу

Пример 1.14. Предполагается поместить 1000 долл. на рублевый депозит. Курс продажи на начало срока депозита 1500 руб. за 1 долл., ожидаемый курс покупки — 1820 руб. (данные середины 1994 г.). Процентные ставки: i = 220% (ставка, которая не была исключительной в операциях коммерческих банков в начале и середине того же года), j = 15%. Срок депозита — три месяца.

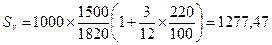долл.

В свою очередь прямое наращение исходной долларовой суммы по долларовой процентной ставке дает

S_v = 1000(1 + 0,25 х 0,15) = 1037,5 долл.

Продолжим анализ и поставим перед собой новую задачу — измерим доходность операции в целом. В качестве измерителя примем простую ставку процентов i _э. Пусть эта ставка характеризует рост суммы P_v до S_v. Для ее расчета воспользуемся формулой (1.14). Теперь ее можно записать как

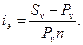
Подставим в эту формулу значение S_v, полученное по (1.16). После несложных преобразований этой формулы получим

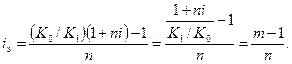(1.18)

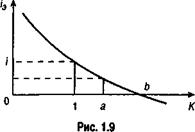
Полученное выражение позволяет сделать ряд заключений. Для этого обратимся к графику (рис 1.9). Предварительно введем величину, характеризующую отношение курсов валюты:

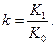(1.19)

С увеличением k эффективность падает. При k = 1 i _э = i, при k > 1 (точка а на оси K) i _э < i, наконец, при k < 1 имеем i _э > i. Найдем теперь критическое значение k (обозначим его как k*), при котором i _э = 0 (точка b на рис 1.9). Из формулы (1.18) следует: k* = ni, что в свою очередь означает

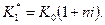(1.20)

Если ожидаемые величины k или К ₁превышают свои критические значения, то операция явно убыточна.

Поскольку в момент заключения контракта величина К ₁является неизвестной, то, вероятно, полезно определить максимально допустимое ее значение, при котором эффективность будет равна существующей ставке по депозитам в СКВ и применение двойного конвертирования не дает никакой дополнительной выгоды. Из равенства множителей наращения

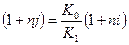(1.21)

следует:

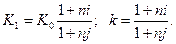(1.22)

Пример 1.15. Продолжим анализ операции из примера 1.14. Пусть речь идет о принятии решения до проведения операции. Величина курса на конец срока неизвестна. Максимально допустимое значение курса составит

руб.

Иначе говоря, если в начале операции ожидают, что курс доллара в рублях в конце срока будет меньше 2241 руб., то выгоднее применить конверсию, если же он будет выше указанной величины, то целесообразнее непосредственный депозит в СКВ.

Вариант Руб.→СКВ→СКВ→Руб. В этом варианте (вариант "б" на рис. 1.8) трем шагам операции соответствуют три сомножителя следующей формулы:

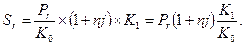(1.23)

Как и в предыдущем варианте, множитель наращения линейно зависит от ставки, но теперь ставки процента по СКВ. Очевидно, что зависимость множителя от конечного курса или его темпа роста также линейная.

Пример 1.16. Допустим, необходимо поместить на валютном депозите сумму в рублях (1 млн.). Остальные условия из примера 1.14. Наращенная сумма в рублях к концу срока составит

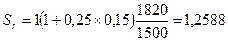млн. руб.

Прямое инвестирование в рублевый депозит дает существенно больше:

S_r = 1(1 + 0,25 х 2,2) = 1,55 млн. руб.

Перейдем теперь к анализу эффективности данной операции и определению критических точек. Доходность операции определяется как

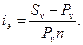
Отсюда

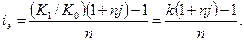(1.24)

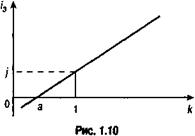
Зависимость показателя эффективности от k линейная. При k = 1 i _э = j (Рис. 1.10), при k > 1 i _э > j, наконец, при k < 1 i _э < j. Найдем теперь критическое значение k* (точка а на рис. 1.9), при котором i _э = 0. Из формулы (1.24) следует:

Минимально допустимая величина k определяется по формуле (1.21).

Пример 1.17. В примере 1.16 прямое инвестирование рублей дает заметно большее наращение. Найдем минимальный темп роста курса, при котором будет получен аналогичный результат при двойном конвертировании рублей. По формуле (1.21) находим

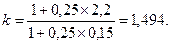
Иначе говоря, этот вариант окажется более эффективным только тогда, когда ожидается прирост курса не менее чем на 50%.

Поиск по сайту: