 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Возмещение премии и накопление дисконта облигаций
Проблема оценки облигаций существует не только тогда, когда облигация покупается или продается на рынке, но и когда она находится у владельца. В общем случае ее цена изменяется во времени даже в такой крайне редкой ситуации, когда рыночная процентная ставка остается постоянной, и уж тем более, если эта ставка изменяется. С приближением даты погашения увеличивается современная стоимость суммы, получаемой при погашении облигации, одновременно уменьшается современная стоимость будущих поступлений по купонам. Какой бы ни была цена до погашения, в конце срока цена облигации равна номиналу или некоторой заранее фиксированной выкупной цене.
Проследим, к каким изменениям в цене или курсе облигаций приводит ход времени. Для этого вернемся к формуле (11.7) и запишем ее для некоторого момента t после выпуска облигации:
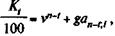t = l, 2,..., n,
где Kt — курс в момент t (после очередной выплаты процентов);
n - t — срок, оставшийся до даты погашения.
Для t = n Kt = 100, так как считаем, что проценты в этот момент уже получены.
Нетрудно установить, что у облигации, купленной с премией, второе слагаемое курса сокращается скорее, чем увеличивается первое. В связи с этим премия и курс в целом уменьшаются с каждым шагом во времени. Такой процесс получил название возмещение премии (amortization).
По определению абсолютный размер премии (дисконта) находится как
E = P - N.
Премия в расчете на курс в момент t составит
et = Kt - 100.
На рис. 11.7 и в табл. 11.7 иллюстрируется процесс возмещения премии на примере облигации с условиями: п = 8, g = 8%, i = 6%.
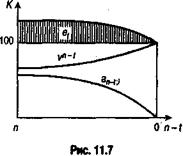
Таблица 11.7
| t | 100vn-t | 100ga8-t;6 | Kt | et |
| 62,74 | 49,68 | 112,42 | 12,42 | |
| 66,51 | 44,66 | 111,17 | 11,17 | |
| 70,50 | 39,34 | 109,83 | 9,83 | |
| ... | ||||
| 94,34 | 7,55 | 101,89 | 1,89 | |
| 100,00 | 100,00 |
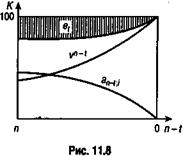
На рис. 11.8 иллюстрируется процесс роста цены за счет накопления дисконта (accumulation). В ходе этого процесса цена и курс облигации увеличиваются во времени, поскольку на каждом шаге во времени рост первого слагаемого перекрывает сокращение второго. Процессы изменения курса рассматривались нами на фоне стабильной рыночной ставки. Однако это условие нереалистично. Действительный курс в связи с изменениями процентной ставки отклоняется от "идеального", динамика которого представлена на рис. 11.7 и 11.8.
Поиск по сайту: