 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Анализ позиции продавца
Определение суммы векселя. Продавец должен получить при учете векселей сумму, равную цене товара. Соответственно анализ для него заключается в определении суммы, которая должна быть указана на векселях. Если окажется, что учет векселей дает величину, меньшую, чем оговоренная цена, то продавец должен заранее поправить положение. Обычно на практике для этого повышают исходную цену. Как показано ниже, альтернативой может служить повышение ставки процентов за кредит. Ясно, что какой бы путь ни был принят, повышение исходной цены или ставки процентов не может быть произвольным.
Сумма, проставленная на векселе (Vt),состоит из двух элементов: суммы, погашающей основной долг (цену товара), и процентов за кредит. Последние определяются двумя способами:
а) проценты на остаток задолженности; в этом случае срок, за который они начисляются, начинается с момента погашения предыдущего векселя;
б) проценты на сумму долга, включенную в вексель; в этом случае срок исчисляется от начала сделки и до момента погашения векселя.
Рассмотрим оба способа для случая, когда долг погашается равными суммами. Введем обозначения:
п — число векселей или периодов;
i — ставка простых процентов за период, под которую производится кредитование;
d — простая учетная ставка, используемая банком при учете векселей;
P — цена товара (если условия операции предусматривают выплату аванса, то последний вычитается из цены и далее не принимается во внимание. Иначе говоря, под P в этом случае будем понимать цену за вычетом аванса).
Вариант а. Погашение основного долга производится равными суммами, соответственно в каждый вексель записывается сумма P / п. Что касается процентов за кредит, то они образуют ряд:
 t = l, 2,..., n.
t = l, 2,..., n.
Сумма векселя, погашаемого в момент t, составит
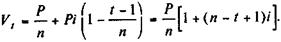 (10.1)
(10.1)
Общая сумма начисленныхпроцентов равна
 (10.2)
(10.2)
Наконец, сумма портфеля векселей составит
 (10.3)
(10.3)
Вариант б. В этом случае по определению
 t = l, 2,..., n. (10.4)
t = l, 2,..., n. (10.4)
Сумма процентов за весь срок находится как
 (10.5)
(10.5)
Получен тот же результат, что и в формуле (10.2). Различие между вариантами, как показано в примере 10.1, заключается в распределении процентов по периодам.
Пример 10.1. В уплату за товар P = 1 млн. руб. выписано четыре векселя с погашением по полугодиям. Ставка процентов за кредит — 10% годовых (простых). Таким образом, i = 5%, n = 4, P /4 = 250 тыс. руб. Определим процентные платежи и суммы векселей двумя методами (все показатели в тыс. руб.).
Таблица 10.1
| T | Р/п | Вариант а | Вариант 6 | ||
| % | Vt | % | Vt | ||
| 50,0 | 300,0 | 12,5 | 262,5 | ||
| 37,5 | 287,5 | 25,0 | 275,0 | ||
| 25,0 | 275,0 | 37,5 | 287,5 | ||
| 12,5 | 262,5 | 50,0 | 300,0 | ||
| Итого: |
Как видим, сумма процентов в обоих вариантах расчета одинакова. Однако распределение платежей противоположное: в в а ри а нте а они уменьшаются, в варианте б растут. Для покупателя вариант б на первый взгляд представляется более привлекательным. Однако, как будет показано ниже, продавец при этом несет некоторые потери.
Корректировка условий продажи. При учете портфеля векселей в банке продавец получит некоторую сумму A. Если применяется простая учетная ставка, как это обычно и делается, то
 t = l, 2,..., n. (10.6)
t = l, 2,..., n. (10.6)
Величина A представляет собой современную величину всех платежей по векселям.
Поскольку сумма на векселе определяется двумя способами, найдем величину A для каждого из них.
Вариант а. В этом случае

 (10.7)
(10.7)
Напомним, что фигурирующие в формулах величины ставок i и d относятся к интервалам между двумя датами погашения векселей.
Для преобразования (10.7) необходимо определить следующие суммы:
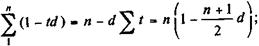

Подставим полученные суммы в формулу (10.7). После ряда преобразований получим
 (10.8)
(10.8)
Обозначим сумму в квадратных скобках через z 1. Очевидно, что если величина z 1 меньше 1, то продавец получит сумму, которая меньше договорной цены P. Наиболее простой путь избежать потерь— повысить цену в 1 /z 1раз. Корректировочный множитель позволяет точно определить необходимуюпоправку и, кроме того, дает возможность проследить влияние всех воздействующих факторов. В редком случае, когда z 1 = 1 и нет необходимости в корректировке, продавец получает при учете векселей оговоренную сумму.
Не надо забывать, что после корректировки цены необходимо вернуться к задаче определения сумм векселей уже для новой цены товара.
Пример 10.2. По данным примера 10.1 в случае, когда учетная ставка 9,5% годовых, получим следующее значение коэффициента z 1:
z 1 = 1 +  = 0,994375.
= 0,994375.
Таким образом, если все условия сделки останутся без изменений, то продавец получит несколько меньшую сумму вместо оговоренной цены — 1 млн. руб. Повышение цены на  = 1,0056568 компенсирует потерю продавца. Суммы векселей после корректировки составят 301, 697; 289, 126; 276, 566; 263, 984. Учет этих векселей по ставке 4,75% за полугодие дает в сумме 1 млн. руб.
= 1,0056568 компенсирует потерю продавца. Суммы векселей после корректировки составят 301, 697; 289, 126; 276, 566; 263, 984. Учет этих векселей по ставке 4,75% за полугодие дает в сумме 1 млн. руб.
Вероятно, представляет практический интерес соотношение процентных ставок, при которых продавец не будет нести потери. Из равенства (10.8) следует, что последнее условие выполнимо в случае, когда

в силу чего
 (10.9)
(10.9)
 (10.10)
(10.10)
где d * и i * — предельные значения ставок, при которых покупатель не несет потерь, иначе говоря, при которыхполучаемая им сумма равна цене. Повышение платы за кредит до уровня i * полностью балансирует условия сделки. Разумеется, что суммы векселей при этом несколько повысятся. В свою очередь, d * представляет собой барьерное значение учетной ставки.
Пример 10.3. Каков должен быть уровень процентной ставки за кредит для того, чтобы покупатель не понес ущерба в операции а форфэ при условии, что d = 4,75% (данные примера 10.1, вариант а расчета сумм векселей). В этом случае
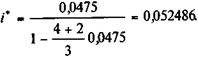
Таким образом, повышение годовой ставки кредита до 10,4972% полностью компенсирует потерю продавца.
Вариант б. Рассмотрим теперь метод расчета корректирующего множителя для случая, когда сумма векселя определяется по варианту б. Напомним, что интервалы между датами погашения векселей одинаковые, применяются простые ставки процентов по кредиту и учетные ставки. По определению
 t = l, 2,..., n. (10.11)
t = l, 2,..., n. (10.11)
После ряда преобразований этого выражения получим
 (10.12)
(10.12)
Сумму в квадратныхскобках обозначим z 2.Смысл этого множителя раскрыт выше. Корректирующий цену множитель в этом случае равен 1/ z 2.
Пример 10.4. Определим по данным примера 10.1 (вариант б расчета сумм векселей) сумму, которую получит покупатель при условии, что d = 4,75%. В этом случае согласно формуле (10.12)
z 2 = 1 +  = 0,988437.
= 0,988437.
Корректирующий исходнуюцену множитель равен 1 / 0,988437 = = 1,0116977. Как видим, z 2< z 1и, следовательно, нужна более существенная корректировка цены, чем по варианту а.


В зарубежной финансовой литературе был предложен иной корректировочный множитель, а именно:
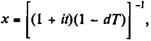
где t и T - средние сроки начисления процентов и векселей. Указанные средние сроки несколько различаются, так как при их расчете применяются разные методы: величина t определяется как простая средняя из сроков платежей; T — как средняя взвешенная этих же сроков с весами, равными Vt. Можно доказать, что данный метод определения корректировочного множителя дает точно такой же результат, как в случае, когда суммы векселей определяются методом б.
Проследим теперь зависимость корректировочных множителей от каждого из параметров, характеризующих условия сделки, — i, d и п. Обозначим эти множители как Z. При увеличении i множитель Z уменьшается. Этот процесс более заметен при низких значениях i, чем при высоких. На рис. 10.1 показана зависимость z от i.
Влияние изменения учетной ставки противоположно влиянию динамики ставки процентов. С ростом d коэффициент Z увеличивается. На рис. 10.2 показана зависимость Z от d при фиксированных значениях i и п.
Что же касается влияния числа платежей n на множитель Z, то очевидно, что при i < d рост n приводит к уменьшению z и необходимость в корректировке условий для продавца возрастает.
Из сказанного следует, что для того, чтобы условия сделки не приводили к необходимости значительного увеличения исходной цены, продавец должен стремиться уменьшить отрицательный разрыв между ставкой процентов и дисконтной ставкой. По крайней мере он заранее должен учитывать неблагоприятное воздействие условия i < d.
Перейдем теперь к корректировке условий сделки с помощью изменения ставки процентов за кредит. Такая корректировка для варианта а была сделана выше (см. 10.10). Единственное значение i, при котором продавец не терпит убытки в варианте б, нетрудно определить из условия, согласно которому z 2= 1. Для того чтобы удовлетворить это требование, необходимо выполнение равенства, которое следует из (10.12):

Решим его относительно i:
 (10.13)
(10.13)
Таким образом, при любой ставке процентов, меньшей чем i*, и заданных P, d и n продавец нуждается в корректировке условий, иначе он получит при учете векселя сумму, которая меньше оговоренной цены.
Пример 10.5. По данным примера 10.1 (вариант б) и при условии, что d = 4,75%, находим

Таким образом, у покупателя имеются две возможности для компенсации потерь при учете портфеля векселей — повысить цену товара на 1,0116977 или увеличить ставку за кредит до 11,0787 годовых.
Аналогичным образом найдем значение d, при котором нет необходимости корректировать условия сделки. Получим:
 (10.14)
(10.14)
Пример 10.6. По данным примера 10.1 (вариант б) находим

Корректировка цены и ставки по кредиту приводит примерно к одинаковым конечным результатам, однако обычно наблюдается небольшое различие в сумме векселей. Для иллюстрации сказанного обратимся к примеру.
Пример 10.7. Первоначальные условия сделки: P = 1200 тыс. руб., ставка по кредиту за полугодие — 3%, учетная ставка за полугодие — 4,5%. Проценты начисляются на сумму векселя (вариант б).Выписывается шесть векселей с последовательным погашением по полугодиям. Поскольку i < d, то сразу можно сказать, что необходима корректировка исходных условий. Корректировочный множитель, рассчитанный по формуле (10.12), составит 1,0787196. Таким образом, сумма векселя с поправкой, но без начисленных процентов равна 200 х 1,07872 = 215,74. Суммы векселей с начисленными процентами по ставке 3% показаны в табл. 10.2.
Применив второй метод корректировки, находим

Значения сумм векселей, полученных наращиванием 200 тыс. руб. по ставке 5,59%, также приведены в табл. 10.2.
Таблица 10.2
| Период | Умножение суммы платежа на множитель 1 /z 2 | Повышение ставки процентов до i* | ||
| Сумма платежа | Дисконт | Сумма платежа | Дисконт | |
| 222,22 | 10,00 | 211,18 | 9,50 | |
| 228,69 | 20,58 | 222,36 | 20,01 | |
| 235,16 | 31,75 | 233,54 | 31,53 | |
| 241,63 | 43,49 | 244,72 | 44,05 | |
| 248,11 | 55,82 | 255,90 | 57,58 | |
| 254,58 | 68,74 | 267,08 | 72,11 | |
| Итого | 1430,39 | 230,38 | 1434,78 | 234,78 |
Нетрудно убедиться в том, что при любом методе корректировки продавец получит сумму, равную оговоренной цене (1200), как это и требовалось доказать. Небольшое различие между итоговыми суммами векселей (и дисконта) объясняется тем, что распределение платежей по срокам несколько различается. В первом случае оно более равномерное (минимальная сумма — 222,22, максимальная — 254,58), во втором — первый вексель выписывается на сумму 211,18, последний — на 267,08. Небольшая отсрочка приводит к увеличению общей суммы платежа по векселям, а также суммы дисконта.
Поиск по сайту: