АННУИТЕТ, ИЛИ ФИНАНСОВАЯ РЕНТА

В большинстве коммерческих операций вместо разовых платежей встреча­ется последовательность денежных поступлений или выплат. Серия потоков поступлений или выплат называется потоком платежей. Поток однонаправ­ленных платежей с равными интервалами времени между последовательны­ми платежами в течение определенного количества лет представляет собой аннуитет (финансовая рента).

Денежные поступления при оценке долговых и долевых ценных бумаг, возможных арендных платежей можно представить следующим образом:

CF\ = CF2 =... = CFn = CF. (9.13)

Аннуитеты могут подразделяться по количеству выплат в году, т. е. годо­вые выплаты (1 раз в год) и срочные (ряд выплат в пределах года), а также по количеству начислений процентов в течение года (ежегодно несколько раз в год или непрерывно). По времени наступления платежей различают два типа аннуитета: 1. Обыкновенный (постнумерандо) аннуитет — когда платежи происходят в конце каждого периода.

530 Финансовый анализ

2. Авансовый (пренумерандо) аннуитет — когда платежи происходят в на­
чале каждого периода.

По продолжительности денежного потока различают:

3. Срочный аннуитет — денежный поток с равными поступлениями в те­
чение ограниченного промежутка времени.

Примером срочного аннуитета постнумерандо являются арендные платежи, за пользование имуществом, землей и т. п., которые регулярно поступают по истечении очередного периода. В качестве примера срочного аннуитета пренумерандо можно представить схему периодических денежных вкладов на банковский счет в начале каждого месяца с целью наполнения определен­ной суммы, необходимой для решения конкретной задачи.

1. Бессрочный аннуитет — когда денежные поступления продолжаются достаточно длительное время.

Будущая стоимость обыкновенного аннуитета рассчитывается по следую­щей формуле:

(9.14)

где CF — денежные поступления аннуитета; F ² — коэффициент наращения будущей стоимости аннуитета.

Для денежного потока из n периода будущая стоимость авансового ан­нуитета равна:

(9.15)

Для определения суммы, которую необходимо депонировать в конце каж­дого периода для того, чтобы через заданное число периодов остаток составил необходимую величину, используется функция, называемая фактор фонда возмещения:

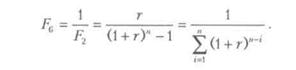
(9.16)

Данный фактор учитывает процент, получаемый по депозитам. Сумма ежегодного вклада составит:

Финансовый анализ 531

(9.17)

где А — стоимость поступлений по истечении срока вложений.

Формула (9.17) применяется для определения суммы, которую следует ежегодно вкладывать на депозитный счет в банк, чтобы через определенное количество лет получить заданную стоимость.

Часто в тех случаях, когда вплоть до истечения срока кредитного договора (долгового обязательства) кредитору выплачивается только процент, заем­щики для погашения основной суммы кредита создают специальные фонды возмещения. В каждый период должник вносит в отдельный фонд сумму, которая вместе с начисляемым на нее процентом должна обеспечить погашение основной части кредита.

Пример 3. Чтобы получить 800 тыс. грн. в конце четырехлетнего перио­да при нулевом проценте, необходимо депонировать 800: 4 = 200 тыс. грн. Если процентная ставка составит 10 %, тогда можно депонировать

тыс. грн. в конце каждого года.

Разница четырех взносов (524,2 тыс. грн.) и полученной суммы составит 275,8 тыс. грн.

Настоящая стоимость обыкновенного аннуитета для денежного потока из п периодов рассчитывается по формуле:

Отдельные элементы денежного потока относятся к разным временным интервалам, поэтому их суммирование искажает реальную доходность инвести­ций. Приведение денежного потока к одному моменту времени осуществляется при помощи функции, называемой текущей стоимостью аннуитета.

Текущая стоимость обыкновенного аннуитета определяется по формуле:

где F₄ — коэффициент дисконтирования настоящей стоимости аннуитета.

Пример 4. В результате осуществления инвестиционного проекта ежегодные доходы в течение 5 лет будут составлять по 500 тыс. грн.

532 Финансовый анализ

Текущая стоимость денежных потоков составит:

В результате дисконтирования дохода за каждый период получим:

454,5 + 413,2 + 375,7 + 341,5 + 310,5 - 1895,4 тыс. грн.

В тех случаях, когда денежные поступления приходят в начале периода, настоящая стоимость авансового аннуитета для денежного потока из п перио­дов рассчитывают следующим образом:

(9.20)

Формула (9.20) применяется для определения текущей стоимости, если доходы, получаемые за каждый і-й период, равны. При неравенстве доходов по временным периодам их получения рассчитывается дисконтированная стоимость за каждый период.

Для определения дохода, который необходимо получать ежегодно, чтобы возместить (окупить) инвестиции за определенный период времени с учетом процентной ставки, используется функция погашения кредита:

(9.21)

Формула (9.21) применяется для определения суммы, которую необходимо ежегодно (ежеквартально) вносить в банк для погашения кредита и процентов по нему.

Ежегодный доход (аннуитет) определяется умножением суммы инвестиций на множитель F5:

(9.22)

где 1 С — начальная сумма инвестиции (вложений).

Пример 5. Инвестиции в проект составили 900 тыс. грн. Чтобы окупить инвестиции в течение 5 лет и получить доход в размере 10 % годовых, еже­годный денежный поток (аннуитет) должен составить:

Финансовый анализ 533

Настоящая стоимость бессрочного аннуитета определяется по формуле:

(9.23)

Бессрочным называется такой денежный поток, при котором денежные поступления продолжаются весьма длительное время (например, аренда на 50 лет и более).

При коэффициент

Формула (9.23) показывает максимальную цену, которую инвестор согла­сен заплатить за бессрочные денежные поступления. Для этого в числителе используют размер годовых поступлений, а в знаменателе в качестве коэф­фициента дисконтирования обычно принимается гарантированная процентная ставка (например, процент по государственным ценным бумагам).

Поиск по сайту: