 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Качуровський М.0., Тарєлкін Ю.П., Цикін В.0
Ступінь  з комплексним показником
з комплексним показником  визначається рівністю:
визначається рівністю:

Можна довести, що
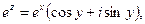
тобто
 (5.13)
(5.13)
Зокрема, при  отримується відношення
отримується відношення
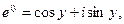 (5.14)
(5.14)
яке називається формулою Ейлера.
Для комплексних показників залишаються в силі основні правила дій з показниками: при множенні чисел показники додаються, при діленні – віднімаються, при піднесенні до ступеня –перемножуються.
Показникова функція має період, який дорівнює 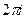 , тобто
, тобто  . Зокрема, при
. Зокрема, при  одержується відношення
одержується відношення  .
.
Тригонометричну форму комплексного числа  можна замінити показниковою формою:
можна замінити показниковою формою:
 (5.15)
(5.15)
Множення, ділення, піднесення до цілого додатного ступеня та добування кореня цілого додатного ступеня для комплексних чисел, заданих в показниковій формі, виконуються за наступними формулами:
 (5.16)
(5.16)
 (5.17)
(5.17)
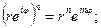 (5.18)
(5.18)
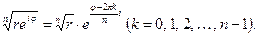 (5.19)
(5.19)
Приклади. 5.18. Знайти показникову форму чисел: 1)  ; 2)
; 2)  .
.
… 1) для заданого числа  знаходимо
знаходимо  ,
, 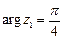 , тобто
, тобто  ;
;
2) для заданого числа  знаходимо
знаходимо  ,
, 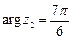 , тобто
, тобто  . †
. †
5.19. Знайти алгебраїчну форму чисел: 1) 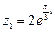 ; 2)
; 2)  ; 3)
; 3)  .
.
… 1) За умовою маємо  ;
;
2) з умови маємо  ;
;
3) маємо  . †
. †
5.20. Знайти добуток 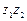 і частку
і частку  комплексних чисел та записати результати в тригонометричній формі: 1)
комплексних чисел та записати результати в тригонометричній формі: 1)  ;
;  ; 2)
; 2)  ;
; 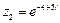 .
.
… 1)  ;
;
 ;
;
2)  ;
;
 †
†
5.21. Обчислити 1) 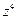 ; 2)
; 2)  , де
, де  , та представити результати в тригонометричній формі.
, та представити результати в тригонометричній формі.
… 1)  ;
;
2)  .
.
 ;
;
 ;
; 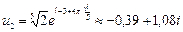 ;
;  ;
;
 . †
. †
Формула Ейлера (5.14) встановлює зв’язок між тригонометричними функціями і показниковою функцією. Замінивши в ній у на 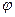 і на
і на  , отримаємо
, отримаємо

Додаючи і віднімаючи ці рівності, отримаємо
 (5.20)
(5.20)
 (5.21)
(5.21)
Ці дві прості формули, які також називають формулами Ейлера, виражають тригонометричні функції через показникові і дозволяють алгебраїчним шляхом отримати основні формули тригонометрії.
| ´ | Питання для самоперевірки |
1. Чому виникла необхідність введення поняття комплексного числа?
2. Що називається комплексним числом; його уявною, дійсною частиною?
3. Коли два комплексні числа вважаються рівними; протилежними?
4. Які два комплексних числа називаються спряженими? Запишіть властивості взаємно спряжених чисел.
5. Що називається алгебраїчною формою комплексного числа? Сформулюйте алгоритми додавання, віднімання, множення і ділення комплексних чисел, записаних в алгебраїчній формі?
6. В чому полягає геометрична інтерпретація комплексних чисел?
7. Що являє собою модуль та аргумент комплексного числа? Які є властивості модуля? В чому полягає особливість аргумента комплексного числа?
8. Як записується тригонометрична форма комплексного числа? Чи будь-яке комплексне число можна записати в тригонометричній формі?
9. За якими формулами відбувається перехід від алгебраїчної форми комплексного числа до тригонометричної?
10. Запишіть формули, які дозволяють оперувати (додавати, віднімати, множити, ділити, підносити до ступеня, добувати корінь) комплексними числами, записаними в тригонометричній формі.
11. Яка форма комплексного числа називається показниковою? Як додати, відняти, помножити, поділити, піднести до ступеня, добути корінь з комплексного числа, записаного в показниковій формі?
12. На понятті якої функції базується формула Ейлера? Де, окрім теорії комплексних чисел, ця формула має застосування?
| @ | Вправи |
1. Розв’язати квадратні рівняння:
1)  ; ;
| 2)  ; ;
| 3) 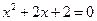 ; ;
|
4)  ; ;
| 5)  ; ;
| 6) 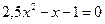 . .
|
2. Побудувати точки, які відповідають даним комплексним числам:
1) –1; 2) і; 3)  ; 4) –3 і; 5) 2–3 і; 6) -4–2 і; 7) 3+ і; 8) -6+2 і; 9) 2+2 і; 10) -2+2 і; 11) -2–2 і.
; 4) –3 і; 5) 2–3 і; 6) -4–2 і; 7) 3+ і; 8) -6+2 і; 9) 2+2 і; 10) -2+2 і; 11) -2–2 і.
3. Знайти суму, різницю, добуток і частку комплексних чисел 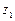 і
і  та зобразити геометрично дані числа і результати операцій:
та зобразити геометрично дані числа і результати операцій:
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 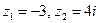 ;
;
5)  ; 6)
; 6)  .
.
4. Що являє собою геометрично множина всіх комплексних чисел 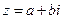 , у яких
, у яких
1) а =2; 2)  ; 3)
; 3)  ; 4)
; 4)  та
та  ; 5)
; 5) 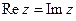 ; 6)
; 6) 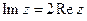 .
.
5. Подати наступні комплексні числа в тригонометричній формі:
1) 1; 2) –1; 3) і; 4) – і; 5)  ; 6)
; 6)  ; 7)
; 7)  ; 8)
; 8)  ; 9)
; 9)  .
.
6. Дано числа 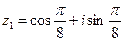 ,
,  ,
, 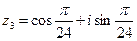 . Обчислити:
. Обчислити:
1) 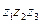 ; 2)
; 2)  ; 3)
; 3) 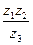 ; 4)
; 4)  .
.
7. Піднести до ступеня: 1) 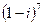 ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
8. Добути корені та результат зобразити на комплексній площині:
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ; 5)
; 5) 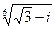 ; 6)
; 6)  .
.
9. Записати в показниковій формі: 1) –1– і; 2)  ; 3) –3; 4) 2 і; 5)
; 3) –3; 4) 2 і; 5)  ; 6)
; 6)  .
.
10. Знайти тригонометричну та алгебраїчну форму комплексних чисел:
1) 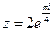 ; 2)
; 2)  ; 3)
; 3) 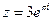 ; 4)
; 4)  ; 5)
; 5)  ; 6)
; 6)  .
.
11. Обчислити добуток  та частку
та частку  комплексних чисел та записати результати в алгебраїчній формі:
комплексних чисел та записати результати в алгебраїчній формі:
1)  та
та  ; 2)
; 2)  та
та  .
.
12. Знайти  і
і 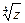 , представити результати в алгебраїчній формі та зобразити їх на площині: 1)
, представити результати в алгебраїчній формі та зобразити їх на площині: 1)  ; 2)
; 2) 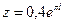 ; 3)
; 3)  ; 4)
; 4)  ; 5)
; 5)  ; 6) z= –16.
; 6) z= –16.
Качуровський М.0., Тарєлкін Ю.П., Цикін В.0.
Поиск по сайту: