ТИПОВЫЕ ПРЕДСТАВЛЕНИЯ СЛОЖНЫХ СИСТЕМ -СУБЪЕКТОВ И ОБЪЕКТОВ МЕНЕДЖМЕНТА

Нельзя эффективно управлять объектом «вообще». Менеджер для принятия решений должен обладать опреде­ленной информацией о структуре, параметрах и других ха­рактеристиках субъекта и объекта управления. Информаци­ей при этом могут считаться только те данные, которые снимают неопределенность в знании о субъекте и(или) объекте с точки зрения конкретной задачи менеджмента. Другие данные являются своеобразным «шумом» и способны не только затруднить, повысить стоимость решения задачи менеджером, но и спровоцировать неверное решение.

Менеджеру приходится искать компромисс между риском отбросить полезную информацию и понести излиш­ние затраты времени и сил на обработку данных, инфор­мацией не являющихся.

Типовые представления сложных систем - это мини­мальный объем информации об объекте и субъекте, позво­ляющий корректно решать задачи их менеджмента.

Практическая польза типовых представлений состоит в сокращении затрат на выбор типа менеджмента, метода прогнозирования, разработку прогнозной модели, выбор метода планирования эксперимента и другое. Типовое пред­ставление позволяет сократить или избежать затрат на раз­работку серии гипотетических поисковых (предварительных) моделей. Оно обеспечивает неразрывность процесса предмодельных исследований и структуризации информации при подготовке прогнозной модели.

Типовые представления можно разделить на два класса: кибернетические, то есть абстрагирующиеся от структуры представляемого объекта, и некибернетические, то есть пред­ставляющие структуру объекта.

Основные требования к объему информации при ти­пизации представлений ОПС:

1) достаточность для разработки модели и решения по­ставленной задачи;

2) минимальный объем информации (минимальная размерность модели), что диктуется необходимостью уменьшения затрат на разработку модели и прогнозиро­вание.

Наиболее часто при диагностике проблемы, прогнози­ровании и решении задач технико-экономического анализа используют следующие отражающие структуру объекта ти­повые представления:

- функционально - декомпозиционное представление;

- представление в виде контуров обслуживания;

- агрегативно - декомпозиционное;

- представление кибернетического типа в виде модели «параметр - поле допуска», абстрагирующееся от структуры

объекта.

Функционально-декомпозиционное представление/9/ следует

за предметным описанием ОПС.

Исходя из располагаемой на ранних этапах разработ­ки информации, в это представление целесообразно вклю­чить сведения об условиях и целях функционирования, то есть о выполняемых функциях. В таком представлении уз­ловым понятием является понятие «функция сложной системы».

Выделим три типа таких функций.

Обозначив {F} - конечное множество функций ОПС, выделим в нем три непересекающихся подмножества: {F^T} -подмножество функций цели; {F^Y} - подмножество функций адаптации; {F^v} - подмножество функций живучести.

Функцией цели Fi^T назовем однозначное отображение i-того элемента К-разбиения множества условий эксплуата­ции Yi € Y; Yi ∩ Yj =0 в соответствующий элемент Pi множества целей функционирования {Р}:

Fi: Yi → P i

Перечень функций цели системы удобно задавать в виде таблицы функциональных отображений. В первом столбце этой таблицы помещают номера функций цели, во втором - формальное описание i-того элемента К-разбиения множества условий эксплуатации, в третьем - описание i-той цели функционирования. В четвертом столбце может помещаться время реализации функций цели.

В предметном смысле функция цели агрегирует то, что должна сделать система для достижения цели функцио­нирования и то, с какими параметрами она должна это сделать. В процессе функционирования системы любая из функций может принимать два значения: 1 - при нормаль­ном функционировании, 0 - в противном случае.

Кроме того, могут изменяться условия функциониро­вания или состояния системы вследствие отказа подсистем.

Функцией адаптации Fij^Y назовем отображение изме­нения условий функционирования в изменение цели функ­ционирования:

F ij: (Yi → Yj) (Pi → Pi) (Fi → Fj)

t t ц t р

где: t - момент изменения условий функционирования;

1_Ц - интервал времени системного выбора цели системы, соответствующей условиям функционирования;

t_p - интервал времени реконфигурации функции цели.

Условия функционирования системы могут изменяться как естественным образом (например, погодные условия), так и в результате случайных или умышленных действий человека (например, рыночных стратегий конкурентов).

Функцией живучести назовем отображение изменения состояния системы вследствие отказа или повреждения под­систем в изменение цели ее функционирования:

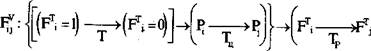
в общем случае:

t ≠ Т; t_ц ≠Т_ц; tp≠

где: Т, Т_ц, Т_Р –

обозначения, аналогичные ранее введенным.

Подмножества функций адаптации и живучести мо­гут быть заданы в виде квадратных таблиц, номера строк и столбцов которых соответствуют номерам функ­ций цели. На пересечении строки и столбца проставляет­ся «+1» (или параметры агрегата, обеспечивающего пере­ход), если возможен переход от выполнения функции цели с номером строки к выполнению функции цели с номером столбца, и «О» - в противном случае. Назван­ные таблицы функций адаптации и живучести задают отношения достижимости функций цели по условиям применения и живучести соответственно.

В таблице функциональных портретов (таблице функций и элементов) фиксируют участие подсистем в реализации определенных функций цели системы. Номера строк этой таблицы соответствуют номерам функций цели, а номера столбцов - номерам подсистем. На пересечении строки и столбца проставляется «+1», если подсистема участвует в реа­лизации функции цели с номером строки, и «-1» - в противном случае. Вместо «+1» могут проставляться характеристики под­системы, важные с точки зрения задачи разработки.

Представление в виде контуров обслуживания /10/. Контуром называют набор взаимосвязанных элементов, функ­ционирование которых направлено на реализацию алгоритма решения задач управления одним из процессов в системе. При использовании многоконтурного подхода объект управления рассматривается в виде взаимосвязанной совокупности техно­логических процессов, заданных графом G(J,F), где: J - множество процессов, Г - множество технологических связей между J.

Структуру многоконтурной системы можно описать так:

S= S а, Sф, Sи, Sт,Sтп

где: S_a - алгоритмическая подструктура; S ф - функциональная подструктура; Sи - информационная подструктура; Sт - техническая подструктура; Sтп - топологическая подструктура.

Соответствующие подструктуры определяют взаимосвя­занные наборы алгоритмов решения задач управления, функции, информационные массивы, технические средства для выполнения функций контуров управления и обеспече­ния связи между ними. Топологическая подструктура опре­деляет расположение элементов. Например, контур управ­ления качеством образования в ВУЗе включает кафедру, деканат, учебно-методическое управление.

Агрегативно-декомпозиционное представление /11/. При этом рассматривается абстрактная схема функционирования сложной системы, центральным звеном которой является агрегат. Представление агрегата изображено на рис. 1.1.

В каждый момент времени t, принадлежащий интервалу [О,т], агрегат находится в одном из возможных состояний Z(t)

Состояние агрегата в фиксированный момент времени t > to определяется предыдущим состоянием и управляющим воздействием g(T) в соответствии с оператором переходов Н с использованием зависимости:

Z(t)=H[Z(to),g(t)].

Агрегат имеет входные контакты. На них поступают входные сигналы x(t), которые в соответствии с оператором выходов G преобразуются в выходные сигналы y(t):

y(t)=G[Z(t),x(t)].

Агрегатное представление наиболее наглядно и поэтому наиболее часто используется в настоящее время. В качестве агрегата рассматривают станок или группу оборудования. При большом числе агрегатов такое представление стано­вится труднообозримым.

Кибернетическое представление в виде модели «параметр - поле допуска» /12/. При таком представлении считают, что система - объект управления - обладает опре­деленными выходными параметрами. Совокупность значе­ний этих параметров П t), i=l,...,n определяет работо­способность системы. Условие работоспособности соответст­вующего объекта имеет вид:

Пin(0 < П,(1) <Пib(1),

где: П.in, Пiв - верхний и нижний допуски на i-тый параметр.

Эти допуски в количестве 2хп образует некоторое пространство, являющееся n-мерным прямоугольным параллелепипедом. Выход i-того параметра за пределы оговоренных допусков переводит объект управления в области недопустимых или неуправляемых состояний. Это представ­ление не описывает структуру объекта и поэтому может быть использовано для контроля, но не для диагностики состояний этого объекта.

При практическом использовании этих представлений в процессе менеджмента должны быть учтены следующие факторы:

- цели и задачи менеджмента;

- имеющаяся информация об объекте управления, объ­ем которой тесно связан с этапом жизненного цикла ОПС или товара - сложной технической системы;

- имеющиеся в распоряжении время, средства и т. п. для решения стоящей задачи. При анализе объекта высокой сложности рекомен­дуется разрабатывать его представления Последовательно, начиная с более общих (предметное, функционально-декомпозиционное, контурами обслуживания, агрегативно-декомпозиционное, «параметр - поле допуска»), обеспечивая таким образом постепенное и управляемое наращивание информации об анализируемом объекте.

Поиск по сайту: