 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Мотивация инноваций
Принцип неравноценности денег во времени
Важнейшим фактором в анализе финансовых операций является принцип неравноценности денег во времени. Рубль, полученный сегодня, стоит больше рубля, который будет получен в будущем. Поэтому в финансовых операциях, особенно долгосрочных, фактор времени может играть не меньшую роль, чем размеры денежных сумм. Каждый из методов анализа, рассмотренных ниже, учитывает время как одно из важнейших условий.
Если в настоящее время 1 рубль можно инвестировать под заданный процент на заданный период, то через этот период инвестор получит 1 рубль плюс процент.
Проценты - это абсолютная величина дохода от представления денег в долг в любой его форме.
Наращенная сумма ссуды — это первоначальная сумма плюс, начисленные к концу срока ссуды проценты.
S = P+I, (2.6.1)
где S - наращенная сумма ссуды, Р - первоначальная сумма ссуды, I- начисленные к концу срока ссуды проценты.
Процентная ставка наращения - это отношение процентов за год к сумме долга.
Процентная ставка является также измерителем степени доходности любой финансовой операции. В этом случае процентная ставка называется доходностью.
Простая процентная ставка наращения
Простая процентная ставка наращения - это ставка, при которой база начисления всегда остается постоянной.
Проценты / за весь срок ссуды вычисляются по формуле
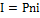, (2.6.2)
где п - срок ссуды в годах, t - простая годовая ставка наращения (десятичная дробь). Подставив выражение для процентов (2.6.2) в (2.6.1), получим формулу простых процентов:
, (2.6.3)
Множитель q = (l + ni) называется множителем наращения простых процентов.
Пример 1. Ссуда 25000 руб. выдана на срок 0,7 года под простые проценты 18% годовых. Определить проценты и наращенную сумму.
Решете. 
.
.
Срок ссуды рассчитывается по формуле:
, (2.6.4)
где t - число дней ссуды, К - временная база или число дней в году. В зависимости от принятой методики используют два типа временных баз:
К = 360 — обыкновенные проценты,
К = 365 (366) - точные проценты.
При расчете срока ссуды при начислении по простым процентам используются три метода:
1. Точные проценты с точным числом дней ссуды. Обозначается 365/365. Количество дней ссуды рассчитывается точно по календарю. Первый и последний день ссуды принимаются за один. К = 365. Метод применяется центральными банками многих стран и крупными коммерческими банками.
2. Обыкновенные проценты с точным числом дней ссуды. Обозначается 365/360. Количество дней ссуды рассчитывается точно по календарю. Первый и последний день ссуды принимаются за один. К = 360. Метод применяется в ссудных операциях коммерческих банков.
3. Обыкновенные проценты с приближенным числом дней ссуды. Обозначается 360/360. Количество дней в каждом месяце принимается равным 30. К= 360. Применяется при промежуточных расчетах.
Пример 2. Ссуда в размере 8 млн. руб. выдана 28 января по 15 июня включительно под простые проценты 22% годовых. Определить величину долга в конце срока тремя методами.
Решение.
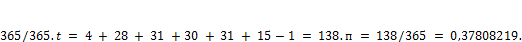
Сложные процентные ставки наращения
Сложная процентная ставка наращения - это ставка, при которой база начисления является переменной, т.е. проценты начисляются на проценты. Предположим, что мы имеем Р руб., которые можно инвестировать по процентной ставке наращения i. Через один год мы будем иметь 
руб. Если повторить этот процесс, инвестировав всю сумму 
, то к концу второго года будем иметь 
. Продолжая процесс, видим, что показатель степени в формуле для наращенной суммы равен количеству лет наращения. Положив это число равным и, получим формулу сложных процентов.
, (2.6.5)
Пример 3. Какой величины достигнет долг, равный 6000 руб., через 4 года при росте по сложной ставки наращения 18,5% годовых?
Решение. S = P(1 + i)n = 6000(l + 0,185)4 = 11831,09 руб.
При наращении по сложным процентам наращенная сумма быстро растет при увеличении числа лет. В таблице 2.6.1 представлен множитель наращения 
в зависимости от числа лет для двух значений ставки.
Таблица 2.6.1.
| n, лет | i = 10% | i = 20% |
| 1,61 | 2,49 | |
| 2,594 | 6,192 | |
| 6,727 | 38,34 | |
| 117,4 | 9100,4 |
Пример 4. Какой величины достигнет долг, равный 8000 руб. через 4,6 года при росте по сложной ставке наращения 20% годовых?
Решение. 
Часто в финансовых операциях в качестве периода наращения процентов используется не год, а, например, месяц, квартал или другой период. В этом случае говорят, что проценты начисляются т раз в году. При этом в контрактах фиксируется не ставка за период, а годовая ставка, которая в этом случае называется номинальной. Сложная процентная ставка наращения является частным случаем номинальной при начислении процентов один раз в году. Если номинальную ставку обозначить через j, то проценты за один период начисляются по ставке 
, а количество начислений равно тп. Наращенная сумма при использовании номинальной процентной ставки наращения определяется по формуле:
, (2.6.6)
Пример 5. Какой величины достигнет долг, равный 15000 руб. через 5,7 года при росте по сложной ставке 16,5% годовых при начислении процентов раз в году и помесячно?
Решение. 
.
Если в формуле (2.6.6), определяющей наращенную сумму при использовании номинальной процентной ставки наращения, периоды начисления процентов постоянно уменьшать, то количество этих периодов в году будет увеличиваться. В пределе при стремлении длительности периодов к нулю их число стремится к бесконечности. Такое начисление процентов называется непрерывным, а процентная ставка при непрерывном начислении называется силой роста. Большое значение непрерывное наращение имеет в анализе сложных финансовых проблем, например, при анализе характеристик ценных бумаг.
Сила роста называется постоянной, если она не изменяется во времени. Если сила роста изменяется во времени, то она называется переменной.
Формула для наращенной суммы при непрерывном начислении процентов для постоянной силы роста δ следует из формулы (6) при стремлении т к бесконечности, т.е.:
.
Т.к. 
, где е - число Эйлера (основание натуральных логарифмов), то, заменяя j на силу роста δ, получим формулу для наращенной суммы при непрерывном начислении процентов
. (2.6.7)
Связь дискретных ставок i и j с силой роста δ находится из равенства множителей наращения дискретных (5), (6) и непрерывной (7) ставок, т.е.
; 
.
Решив эти уравнения, получим:
; 
(2.6.8)
; 
. (2.6.9)
По формулам (2.6.8) и (2.6.9) можно, в частности, зная дискретные ставки ценных бумаг, рассчитать силу роста этих бумаг.
Пример 6. На сумму 15000 руб. начисляются проценты по сложной годовой ставке i = 22% в течение 3,5 лет. Определить силу роста и наращенную сумму при дискретном и непрерывном начислении.
Решение. 
.
Наращенная сумма при непрерывном начислении
.
Наращенная сумма при дискретном начислении
.
Таким образом, как и следовало ожидать, наращенные суммы при дискретном и непрерывном начислениях совпали.
Пусть переменная сила роста изменяется во времени, т.е. St = fit)- В этом случае наращенная сумма определяется соотношением:
.
При дисконтировании суммы S, которая будет выдана через срок и, по ставке дисконтирования i вычисляется современная величина (стоимость) Р суммы S. Используя формулы (2.6.3), (2.6.5), (2.6.6) и (2.6.7) получим соотношения дисконтирования для рассмотренных типов процентов
(2.6.10)
Множители 
называется дисконтными множителями.
Разность 
. (2.6.11)
называется дисконтом с суммы S.
Пример 7. Через 159 дней должник уплатит 8,5 тыс. руб. Кредит выдан под простые проценты 19% годовых. Какова первоначальная сумма долга и дисконт при условии, что временная база равна 360 дней?
Решение.
руб.
руб.
Пример 8. Построить таблицу для дисконтного множителя при сроке ссуды 5; 10; 20; 50 лет и при сложной ставке наращения 10% и 20%.
Решение. Результаты приведены в таблице 2.6.2.
Таблица 2.6.2.
| n, лет | i = 10% | i = 20% |
| 0,621 | 0,402 | |
| 0,386 | 0,162 | |
| 0,149 | 0,026 | |
| 0,00852 | 0,00011 |
Пример 9. Сумма 12000 руб. выплачивается через 2,4 года. Номинальная ставка процентов - 16% годовых. Определить современную стоимость при ежеквартальном начислении процентов.
Решение. 
Учетные ставки
Банк может учесть вексель до наступления срока платежа с дисконтом, т.е. купить его у владельца по цене, которая меньше номинала S, указанного в векселе. Размер дисконта при учете по простой учетной ставке определяется по формуле:
,
где d - простая учетная ставка, п - срок от момента учета до момента погашения. Подставив это значение в соотношение (2.6.11), получим формулу для расчета суммы, выплачиваемой владельцу векселя при учете по простой процентной ставке:
(2.6.12)
Множитель (1 — nd) называется дисконтным множителем. Обычно при расчетах принимают К = 360.
Пример 10. Вексель, имеющий номинальную стоимость 8000руб., учтен в банке по простой учетной ставке 18,5% годовых за 132 дня до его погашения. Определить сумму, полученную владельцем векселя при учете.
Решение.
При использовании сложной учетной ставки каждый раз эта ставка применяется не к первоначальной сумме, как при простой учетной ставке, а к сумме уже дисконтированной на предыдущем шаге во времени. Поэтому сумма, выдаваемая банком при учете векселя, рассчитывается по формулам:
(2.6.13)
Здесь d - сложная учетная ставка.
Пример 11. Вексель на сумму 20000руб., срок платежа, по которому наступает через 1,8 года, учтен по сложной процентной ставке 18% годовых. Определить сумму, полученную владельцем векселя при учете, и дисконт при ежегодном и ежемесячном дисконтировании.
Решение. 
.
.
руб.
Определение срока ссуды и величины процентной ставки
Формулы для определения срока ссуды и величины процентной ставки при начислении по простым и сложным процентам следуют из соотношений (2.6.3), (2.6.5), (2.6.6), (2.6.7), (2.6.12), и (2.6.13). В качестве примеров рассмотрим методы определения срока ссуды и величины простой и сложной процентных ставок наращения. Срок ссуды и величин простой процентной ставки наращения находят, решая (2.6.3) относительно п и i.
(2.6.14)
Срок ссуды и величин сложной процентной ставки наращения определяют из формулы (2.6.5).
(2.6.15)
Пример 12. За какой срок сумма, равная 25000 руб., достигнет 40000 руб. при начислении по сложной процентной ставке 18% годовых?
Решение.
Пример 13. Финансовый инструмент куплен за 25000 руб., его выкупная цена через 1,8 года составит 35000 руб. Определить доходность операции в виде годовой ставки сложных процентов.
Решение.
Эквивалентность процентных ставок
Нами были рассмотрены следующие виды процентных ставок:
♦ простая процентная ставка наращения,
♦ сложная процентная ставка наращения,
♦ номинальная процентная ставка наращения,
♦ сила роста,
♦ простая учетная ставка,
♦ сложная учетная ставка.
Эквивалентными процентными ставками называются любые две из перечисленных выше, которые при замене одной на другую приводят к одинаковым финансовым результатам, т. е. отношения сторон не изменяются в рамках одной финансовой операции.
Определим соотношения эквивалентности между простой процентной ставкой наращения и сложной процентной ставкой наращения. При этом полагаем, что начальные и наращенные суммы при применении рассматриваемых ставок одинаковы. Поэтому для решения поставленной задачи приравняем множители наращения друг к другу. В результате получим:
,
где i - простая процентная ставка наращения, а - сложная процентная ставка наращения, п - срок операции в годах. Решив это уравнение относительно а и i, получим
(2.6.16)
Пример 13. Простая процентная ставка депозита равна 20% годовых, срок депозита 0,5 года. Определить доходность финансовой операции в виде сложной годовой процентной ставки.
Решение. 
.
Найдем соотношения эквивалентности между номинальной процентной ставкой наращения j и сложной процентной ставкой наращения а. В этом случае сложная процентная ставка наращения называется эффективной ставкой процентов. Эффективная ставка процентов — это годовая ставка сложных процентов при начислении раз в году, которая дает тот же результат, что и т - разовое начисление процентов по ставке . Поэтому множители наращения эффективной и номинальной ставок должны быть равны друг другу, т.е.
,
Решив это уравнение относительно 
и 
, получим:
(2.6.17)
Замена в договоре номинальной ставки j при m-разовом начислении процентов на эффективную ставку а не изменит финансовых обязательств участников сторон, т.е. обе ставки эквивалентны в финансовом отношении.
Пример 14. Номинальная ставка процента при начислении один раз в квартал равна 16% годовых. Определить эффективную ставку.
Решение: 
.
Соотношения эквивалентности между номинальной процентной ставкой наращения j и силой роста 5 определяется из соотношения:
.
Отсюда находим:
; (2.6.18)
Соотношения эквивалентности между сложной процентной ставкой наращения а и силой роста 
определяется из (18) при т = 1.
; (2.6.19)
Пример 15. Определить силу роста для сложной процентной ставки наращения 20% годовых.
Решение. 
Эквивалентные процентные ставки для любых двух рассмотренных в этой главе ставок определяются аналогичным образом.
Учет инфляции
Без учета инфляции конечные результаты расчетов денежных потоков являются весьма условными. Рассмотрим некоторые понятия, связанные с инфляционными процессами.
Реальная стоимость С суммы S, обесцененной во времени за счет инфляции, рассчитывается по формуле:
, (2.6.20)
где Ip — индекс цен.
Индекс цен может быть рассчитан, например, по формуле Пааше:
,
где 
- цена j-го товара в исследуемом и базисном периодах соответственно, 
— количество
проданных товаров j в исследуемом периоде, Т - общее количество исследуемых товаров.
Темпом инфляции называется относительный прирост цен за период
, (2.6.21)
Индекс цен за несколько периодов п, следующих друг за другом, вычисляется по формуле
, (2.6.22)
где t - номер периода, Iр ( - индекс цен в периоде t, Ht - темп инфляции в периоде t.
Если ожидаемый темп инфляции величина постоянная в течении п периодов, то формула (2.6.22) приобретает вид
(2.6.23)
Средние за период индекс цен 
и темп инфляции 
находятся по формулам:
,
где п - количество периодов (лет).
Для простых процентов обесцененная инфляцией сумма определяется выражением:
, (2.6.24)
Из (2.6.24) следует, что увеличение наращенной суммы имеет место при выполнении соотношения:
Ставка i*, при которой наращение равно потерям из-за инфляции, определяется из равенства С = Р. Сопоставив это с (2.6.24), находим:
, (2.6.25)
Пример 16. Месячный темп инфляции составляет: а) Н1-12 =4%, б) Н1 =4%, Н2 =3%, Н3 =2%. Для случаев а) и б) найти индекс цен и темп инфляции за 12 и 3 месяца соответственно, а также определить обесцененную наращенную сумму, если на сумму 10000 руб. в течение указанных сроков начислялась простая процентная ставка 50% годовых (К = 360). Определить ставку, при которой наращение равно потерям из-за инфляции. Решение. При решении примера используются формулы (2.6.21) - (2.6.25).
В варианте а) произошла эрозия капитала, а для его увеличения процентная ставка должна превышать 60,1%. В варианте б) капитал вырос в 10294,54/10000 —1,029454 раз или приблизительно на 2,94%.
Для сложных процентов обесцененная инфляцией сумма определяется выражением:
, (2.6.26)
Зависимость обесцененной инфляцией суммы от времени представлена на рис. 2.6.1. Эрозия капитала это обесценивание денег во времени за счет инфляции.
Рис. 2.6.1. Зависимость обесцененной инфляцией суммы от времени
Для компенсации обесценивания денег ставку увеличивают на величину инфляционной премии, являющейся дополнительной доходностью, компенсирующей инфляционные потери. Итоговую ставку называют брутто-ставкой. Выразим величину брутто-ставки r через доходность операции а. Тогда ставку r в формуле (2.6.24) и ставку а в формуле для сложных процентов С = Р(1 + a)n надо считать эквивалентными, т.е. их связь определяется уравнением:
,
где Iр - индекс цен за п лет. Отсюда находим:
(2.6.27)
Для сложных процентов брутто-ставка и доходность определяются соотношением:
(2.6.28)
Из (28) следует, что:
(2.6.29)
При постоянном темпе инфляции при подстановке (2.6.23) в (2.6.28) находим:
.
Отсюда получим связь между брутто-ставкой и доходностью:
(2.6.30)
При |а|<1 и |Ht|<1 имеем r ≈ а + Нt. Таким образом, как следует из формулы (2.6.30), определить брутто-ставку путем сложения доходности операции и темпа инфляции можно только при небольших значениях этих величин.
.
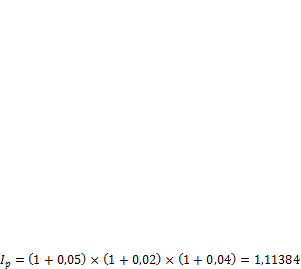По формуле (2.6.27) при п = 3/12 = 0,25 определяем для двух случаев:
.
.
Во втором случае произошла эрозия капитала на 13,95%
Пример 18. Найти сложную процентную брутто-ставку при доходности 15% годовых и годовых темпах инфляции за три года для двух случаев а) H1 = 90%; H2 = 80%; Н3 = 60%,
б) H1=80%=const.
Решение, а) Находим средний темп инфляции за три года:
По формуле (2.6.29) определяем номинальную процентную ставку:
.
в) По формуле (2.630) определяем номинальную процентную ставку для постоянного темпа инфляции:
.
Конверсия валюты
Конверсия (обмен) валюты и временное наращение денег может привести как к прибыли, так и к потерям. Это зависит от величины процентной ставки, от курсов обмена валюты в начале и в конце операции, от инфляции. Рассмотрим, прежде всего, конверсию валюты за счет ее покупки и продажи. Анализ доходности при покупки и продаже валюты можно провести на основе соотношения:
,
где Р - сумма в рублях в начале операции, С - реальная стоимость суммы в рублях в конце операции, K0 и К1 - курс обмена в начале и в конце операции соответственно, имеющий, например, размерность руб./долл., Iр - индекс цен за время операции п. Рублевая сумма Р обменена на валюту (деление на К0), затем через период п лет обменена на рубли (умножение на К1). Для определения реальной стоимости полученной суммы она делится на индекс цен за время операции и, равный Ip. Введем обозначение, Ik — K1 /К0. Тогда полученную формулу можно записать в виде:
(2.6.31)
Для определения доходности а в виде сложной процентной ставки рассматриваемой финансовой операции используется принцип финансовой эквивалентности обязательств. Эквивалентными называются равные друг другу платежи при приведении их к одному моменту времени. В соответствии с принципом финансовой эквивалентности обязательств выражение (2.6.31) можно записать в виде:
,
Отсюда находим формулу для доходности операции:
(2.6.32)
Доходность операции будет равна нулю при выполнении условия Ik = Ip. При Ik > Iр доходность будет больше нуля, а при Ik < Ip - меньше нуля. Поскольку цена покупки валюты и цена ее продажи различаются в один и тот же момент времени, то при расчете доходности за К0 надо принимать цену покупки, аза К1 - цену продажи.
Ход зависимостей Ik и Ip от времени существенным образом зависит от начальной базы. Для построения зависимости курса доллара и темпа инфляции от времени были использованы статистические данные по темпу инфляции и курсу доллара, начиная с 1990 г. по настоящее время. Построенные зависимости курса доллара и темпа инфляции от времени приведены рис. 2.6.2. Из рис. 2.6.2 следует, что курс доллара и индекс цен увеличиваются во времени. В самом начале реформ курс доллара резко подскочил вверх, а индекс цен изменялся медленнее. Затем ситуация изменилась на противоположную, т.е. индекс цен до ноября 1995 г. растет быстрее. Начиная с ноября 1995 г. и до августа 1998 г. значения курса доллара и индекса цен сравнялись относительно базового, и эти значения сравнительно медленно растут с одинаковой скоростью. Начиная с августа 1998 г. равновесие вновь было нарушено. С сентября 1998 г. до января 2000 г. индексы цен и курса доллара изменялись практически с постоянной скоростью. Их разность составляла 3дБ, т.е. индекс курса доллара превышал примерно в два раза индекс цен (без учета инфляции доллара в США). Начиная с середины 2000 г. инфляция растет быстрее курса доллара, т.е. происходит постепенное выравнивание цен.
Если рассматриваемая финансовая операция проводилась в период с середины 2000 г. до середины 2002 г., то индекс 1р рос быстрее, чем индекс 1к и, в соответствии с (2.6.32), эта финансовая операция была убыточной.
Пример 18. Доллары были приобретены по курсу 24 руб./долл. и через 1,2 года проданы по 26,4 руб./долл. (27,6 руб./долл.). Темп инфляции за этот промежуток времени составил 12%. Определить доходность финансовой операции.
Решение. Для приведенных значений отношение курса продажи к курсу покупки составит
.
Индекс цен за 1,2 года равен Iр=1 + Н = 1 + 0,12 = 1,12. Доходности для рассматриваемых случаев:
.
.
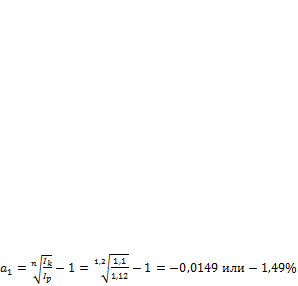В первом случае произошла эрозия капитала, во втором случае капитал возрос.
При наращении процентов с конверсией возможны варианты:
1) руб. — СКВ — наращение — СКВ — руб.,
2) СКВ — руб. — наращение — руб. — СКВ.
Причем наращение может вестись как по простой, так и по сложной процентной ставке наращения. Рассмотрим первый вариант при наращении по сложной процентной ставке. Обозначения используемых здесь величин те же, что и прежде. Если r - сложная годовая ставка наращения СКВ, то уравнение эквивалентности для рассматриваемых условий примет вид:
.
Отсюда находим доходность финансовой операции по первой схеме конверсии валюты с наращением процентов:
(2.6.33)
Пример 19. Для условий предыдущего примера положить сложную ставку наращения СКВ равной 14% годовых.
Решение: 
,
.
Теперь в обоих случаях произошло наращение капитала.
Для второго варианта конверсии валюты с наращением наращенная сумма с учетом инфляции СКВ определяется выражением
.
Индекс «СКВ» показывает, что величина измеряется в денежных единицах выбранной валюты, 1р,СКВ -
индекс цен выбранной валюты за рассматриваемый период, r - сложная рублевая годовая ставка наращения. Из этого выражения находится формула для доходности финансовой операции:
(2.6.34)
Пример 20. Доллары были проданы по курсу 24 руб./долл., а полученная сумма помещена на депозит по сложной процентной ставке 10% (40%) годовых. Через 1,2 года наращенная сумма была истрачена на покупку долларов по курсу 26,4 руб./долл. Темп инфляции доллара за этот промежуток времени составил 4%. Определить доходность финансовой операции.
Решение.
или 25,15% годовых.
Спотовые и форвардные процентные ставки
Спотовая номинальная процентная ставка для периода в n лет - это номинальная ставка для облигаций с нулевым купоном, до погашения которой остается п лет. Облигацией с нулевым купоном называется ценная бумага, по которой не выплачиваются проценты.
Форвардная номинальная процентная ставка - это номинальная спотовая ставка для момента времени 
в будущем (рис. 2.6.3).
Рис. 2.6.3.
Процентные ставки наращения могут самым разнообразным образом изменяться во времени. Примером этих ставок являются безрисковая ставка, доходность облигаций, акций и т.д. На рис. 2.6.4 показаны некоторые возможные изменения процентных ставок от времени.
Рис. 2.6.4.
Рассмотрим метод определения спотовой и форвардной ставок при известной функции процентной ставки наращения от времени. Анализ проведем на примере силы роста и сложной годовой номинальной процентной ставки, начисление процентов по которой производится несколько раз в году.
Пусть в настоящий момент (t = 0) известны спотовая номинальная процентная ставка j0,n для периода n лет и спотовая номинальная процентная ставка j0,𝜏 для периода в т лет, т.е. имеются две спотовые ставки для моментов времени, представленных на рис. 2.6.3. Вкладчик покупает облигацию с нулевым купоном, выпущенную на n лет, которая будет погашена по цене S. Современная стоимость Р этой облигации определяется соотношением:
,
где m - количество начислении процентов в году.
Альтернативой этой финансовой операции является покупка облигации с нулевым купоном, выпущенную на лет, продажа ее через лет и покупка облигации с нулевым купоном на Т = п — 
лет. В последнем случае процентная ставка является форвардной ставкой. В результате этой финансовой операции инвестор должен получить тот же финансовой результат, что и в первом случае, т.е. при затрате суммы Р получить через n лет сумму S. Современная стоимость платежей для альтернативной финансовой операции определяется выражением
,
где j𝜏 - форвардная номинальная процентная ставка.
Приравнивая правые части полученных соотношений, найдем:
(2.6.35)
Обозначив силу роста буквой , в пределе при m→∞, получим:
(2.6.36)
Из соотношений (2.6.35) и (2.6.36) определим связь между номинальной j0 n и непрерывной S0 п спотовыми ставками.
(2.6.37)
Для годовых спотовых ставок (m = 1) имеем:
(2.6.38)
Формулы (2.6.37) совпадают по виду с формулами (2.6.9) и (2.6.8).
Из соотношения (2.6.36) находим формулу для расчета форвардной силы роста:
(2.6.39)
Графики этой функции от 
при различных значениях 
представлены на рис. 2.6.5.
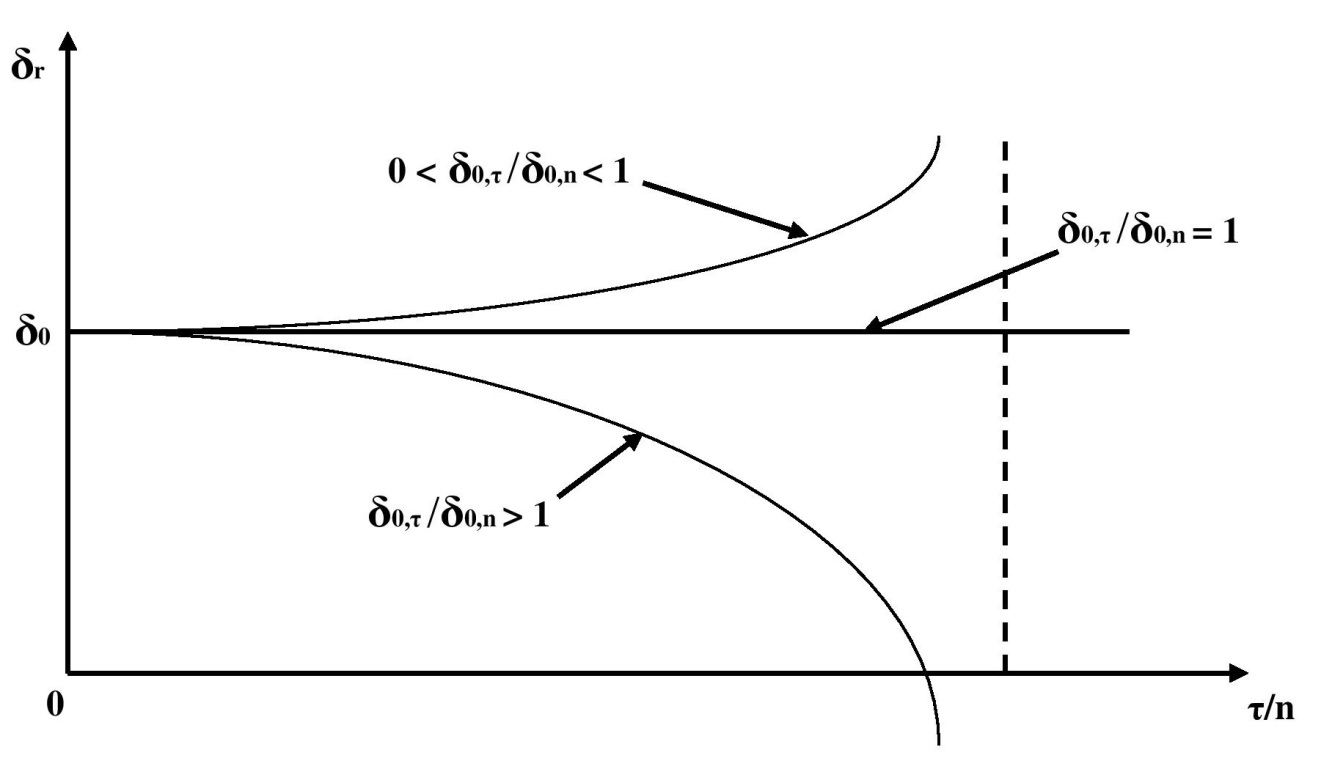
Рис. 2.6.5.
Вернемся к функции процентной ставки наращения от времени. На рис. 2.6.6 показан пример временной зависимости номинальной процентной ставки. Отрезок времени от 0 до n разбит на L равных элементарных отрезков длительностью Δt. Номинальная процентная ставка внутри каждого отрезка постоянна. Например, на отрезке 1 эта ставка равна j1, на отрезке 2 - j2 и т.д. Для поставленных условий долг в момент и определяется соотношением
, (2.6.40)
где Р - первоначальная сумма долга.
Для непрерывного начисления процентов (т → ∞) при замене номинальной ставки j на силу роста δ имеем:
.
При Δt→0 (L→∞) получим:
Рис. 2.6.6.
(2.6.41)
Эту формулу можно получить иначе. Разделим правую и левую части (2.6.40) на Р и прологарифмируем результат:
При Δt→0 (L→∞) получим:
.
Это выражение можно представить в виде:
(2.6.42)
Сопоставив (42) с (41), найдем
(2.6.43)
Для годовых ставок (т = 1) имеем:
(2.6.44)
Здесь i - годовая процентная ставка наращения.
Таким образом, вид формул (2.6.43) и (2.6.44), определяющих связь силы роста наращения и ставки наращения, совпадает с видом формул (2.6.37) и (2.6.38), определяющих связь спотовой силы роста и спотовой ставки.
Перейдя в (2.6.42) к пределу при т → ∞, получим (2.6.41).
Если отрезок от 0 до n разбить на два (0,𝜏) и (𝜏,n), где точка 𝜏 лежит между 0 и n (рис. 2.6.3), то формулу (2.6.41).можно записать в виде:
.
Наращенная сумма, выраженная через форвардную силу роста для момента времени х, по определению форвардной ставки находится из соотношения
Сопоставив два последних выражения, найдем формулу для расчета форвардной силы роста 
в любой произвольный момент 𝜏.
(2.6.45)
Формула для расчета спотовой силы роста следует из (2.6.45) при 𝜏 = 0.
(2.6.46)
Выразим зависимость силы роста наращения от спотовой силы роста. Для этого умножим левую и правую части (2.6.46) на п и, продифференцировав их по n, получим формулу для расчета силы роста наращения в зависимости от спотовой силы роста
(2.6.47)
Проведя вычисления по этой формуле и заменив в результате п на t, получим зависимость силы роста наращения от времени 
.
Из выражения (2.6.47) следует, что если S0 п возрастает при увеличении п, т.е. 
, то 
, если же 
убывает, то 
.
Пример 21. Определить зависимость непрерывной форвардной процентной ставки от времени, если непрерывная спотовая ставка наращения имеет вид
а) 
; b) 
.
Решение. Непрерывную процентную ставку наращения определим по формуле (47).
а) 
b) 
.
Непрерывная форвардная ставка наращения вычисляется по формуле (2.6.45).
;
.
Найдем связь между спотовой номинальной ставкой и номинальной ставкой наращения. Для этих целей во вторую (37) подставим выражение для расчета спотовой силы роста (2.6.46). В результате получим:
.
Подставив сюда первую формулу (2.6.43), найдем:
.
Иначе это выражение можно записать в виде:
. (2.6.48)
Для годовых ставок (m=1) имеем:
(2.6.49)
Контрольные вопросы
1. Назовите известные вам методы выбора инновационной политики и их особенности?
2. Какие существуют методы прогнозирования инноваций и области их применения?
3. Охарактеризуйте основные методы и этапы поиска идеи инновации?
4. Назовите приемы инновационного менеджмента и сферы их использования?
5. Дайте определения бенчмаркингу, инжинирингу, реинжинирингу, фронтированию и мэрджеру?
6. Как используется мотивация для создания и продажи инноваций?
7. Как и для чего производятся финансовые расчеты в инновационном менеджменте?
Поиск по сайту: