Трактування понять “частина” та “дріб” у курсі математики початкової школи. ТМО ознайомлення учнів з поняттям «частина»

1. Яка ж мета ознайомлення учнів початкових класів з дробами? – аналіз методичної літератури, навчальної програми з математики дозволяють твердити, що відомості про дроби включено до програми для того, щоб розширити уявлення молодших школярів про число, сформувати у них конкретні уявлення про частини та дроби, підготувати дітей до вивчення дробів у курсі математики 5-6 класів.

Як же розміщений матеріал, пов’язаний з дробами в курсі математики? -у третьому класі в темі „Таблиця ділення на 4” діти ознайомлюються з такими поняттями як „половина”, „третина чи третя частина”, „четвертина чи четверта частина”, а пізніше при вивченні ділення на 8 „шоста частина”. Слід зазначити, що в цей час символічні позначення (відповідно 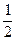, , , 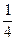) не використовуються. Пізніше в темі „Множення і ділення в межах 1000” учні ознайомлюються з символічними позначеннями частин 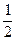, , , 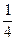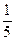тощо та розв’язують текстові задачі на знаходження частини від числа і числа за його частиною. У четвертому класі розглядається тема „Ознайомлення з дробами”.

Успішність роботи вчителя значною мірою залежить від володіння ним ТМО розгляду цього матеріалу. Це, у свою чергу, передбачає необхідність обізнаності вчителя з відповіддю на запитання “Яких же результатів слід досягти вчителеві при вивченні дробів? ” – аналіз вимог державного освітнього стандарту, навчальної програми з математики для початкових класів дозволяють зробити висновок про те, що при вивченні дробів вчитель повинен: 1) створити в учнів конкретні уявлення про процес утворення дробів; 2) сформувати у школярів уявлення про дроби; 3) навчити дітей розуміти такі терміни як дріб, чисельник, знаменник дробу; 4) сформувати в учнів уміння читати і записувати частини та дроби; 5) навчити школярів порівнювати частини та дроби; 6) навчити дітей знаходити частину і дріб числа та число за його частиною; 7) навчити учнів розв’язувати текстові задачі, пов’язані з дробами.

Які ж закономірності слід віднести до ТМО вивчення вказаних питань? – аналіз методичної літератури, вивчення досвіду роботи вчителів-новаторів дозволяють віднести до них наступні: 1) оскільки дослідження науковців засвідчили, що правильні уявлення про частини можуть бути сформовані лише тоді, коли учні своїми руками будуть одержувати частини чи дроби, то цілком обґрунтованим є необхідність використання практичних робіт з моделювання (перегинання, розфарбовування, розрізання, креслення) геометричних фігур; 2) особливості мислення дітей цього віку вимагають використання достатньої кількості наочності, а тому вчитель повинен потурбуватися про забезпечення кожного школяра роздатковим матеріалом: лінійка, кольорові олівці, набір геометричних фігур, смужки, розбірний куб тощо; 3) формування уявлень про частини величини та дроби проходить успішніше, як свідчить досвід роботи вчителів-новаторів, якщо систематично використовується прийом протиставлення та зіставлення рівних і нерівних частин; 4) для того, щоб в учнів формувалися правильні уявлення про частини та дроби, вчитель зобов’язаний забезпечити різноманітність використовуваних об’єктів за розмірами, кольором, матеріалом виготовлення тощо; 5) оскільки проведені дослідження переконливо доводять, що формування уявлень про частини та дроби полегшується, якщо у дітей створені яскраві й конкретні уявлення про процес їхнього одержання, то особливістю вивчення цього матеріалу є ілюстративність, тому слід широко використовувати розгляд та аналіз малюнків; 6) формування уявлень про частини та дроби не можна обмежувати лише уроками вказаних тем, а систематично включати відповідні вправи на наступних уроках; 7) оскільки успішність формування поняття про дроби значною мірою залежить від конкретних образів частин величини, від практичного уміння їх утворити в результаті поділу предметів чи геометричних фігур на потрібну кількість рівних частин, то перед вивченням теми “Дроби” вчитель повинен актуалізувати опорні знання, уміння й навички про величини; 8) оскільки рівень уявлень учнів про частини та дроби, сформованість умінь поділяти фігури на частини різні, то це з необхідністю вимагає використання у навчальному процесі особистісно-орієнтованого підходу.

Чи знайомі діти з поняттям „частина”? – так, бо ще до школи у повсякденному житті вони зустрічалися зі словами „півкілограма”, „третя частина городу”, „чверть години” тощо. Крім цього, вони зустрічалися в процесі ігор з необхідністю проводити операцію ділення на рівні чи нерівні частини. Оскільки ці уявлення можуть бути неповними, неточними чи навіть неправильними, то завдання вчителя полягатиме в тому, щоб виявити ці уявлення, уточнити, систематизувати та узагальнити. Саме це робитиме вчитель на підготовчому етапі.

ТМО навчання передбачають проведення підготовчої роботи до вивчення нового матеріалу. Саме тому вчитель повинен на підготовчому етапі виявити рівень володіння матеріалом, який буде необхідний для успішного засвоєння учнями нового. Таким чином, мета цього періоду полягає в актуалізації опорних знань, умінь і навичок, що надасть можливість усунути зайві труднощі. Тут же доведеться уточнювати або ж навіть і виправляти деякі уявлення дітей. Саме з цієї причини робота на підготовчому етапі повинна носити яскраво виражений особистісно-орієнтований характер. Цей етап розпочинається з перших уроків математики і продовжується до вивчення теми “Частини величини”.

Програмою з математики для початкових класів передбачається ознайомлення з такими питаннями: 1) утворення, позначення та порівняння частин; 2) знаходження частини числа; 3) знаходження числа за його частиною. Успішність вивчення цієї теми значною мірою залежатиме від обізнаності вчителя з результатами, яких він повинен досягти при її розгляді. Яких же результатів повинен добитися вчитель при вивченні цієї теми? – аналіз вимог навчальної програми, методичних посібників для вчителів, діючих підручників дозволяє твердити, що:

1) учні повинні мати уявлення про процес утворення частини від цілого предмета чи сукупності предметів;

2) школярі повинні вміти читати і записувати частини із знаменником в межах ста;

3) діти повинні вміти знаходити частину числа та число за його частиною;

4) учні повинні вміти розв’язувати задачі, пов’язані з частинами (на знаходження частини числа і числа за його частиною);

5) школярі повинні вміти порівняти частини за величиною.

Що ж є першим кроком у формуванні початкових уявлень про частини? – нагромадження уявлень про поділ фігур на рівні частини. Які ж предмети краще використовувати для цього? – ті, які часто зустрічаються дітям в навколишньому житті. Так, наприклад, учні по декілька раз в день чують „ чверть години”, „півкілограма”, „третя частина дороги” тощо. Як свідчать аналіз методичної літератури, вивчення досвіду роботи вчителів-новаторів можна рекомендувати такий план вивчення теми: 1) виявлення уявлень про дану частку; 2) утворення частин величини шляхом ділення на рівні частини предметів; 3) запис частин; 4) порівняння частин.

Для з’ясування уявлень учнів про половину можна запропонувати учням дати відповідь на такі запитання: Як одержати половину яблука, круга, прямокутника, квадрата, смужки тощо? Аналогічно можна з’ясувати уявлення учнів про інші частини величини. Перед тим як перейти до розгляду другого пункту плану зауважимо, що роботу з ознайомлення з частинами потрібно організувати так, щоб створити у дітей яскраві і конкретні уявлення про процес одержання частин. Саме тому особливістю методики вивчення частин є конкретність, наочність, ілюстративність. Наочність повинна бути оперативною, дійовою. Оскільки при вивченні цієї теми корисно провести якомога більше практичних робіт, то потрібно забезпечити кожного школяра роздатковим матеріалом: лінійка, кольорові олівці, набір геометричних фігур, смужки, розбірний куб.

Дослідження науковців показують, що правильні уявлення про частини будуть сформовані лише тоді, коли учні своїми руками будуть одержувати половину, третину тощо. Із наявного у кожного учня роздаткового матеріалу вчитель пропонує вибрати два однакових круга і поділити один із них на дві рівнім частини. При цьому вчитель показує, як перегнути круг. Рівність частин корисно ілюструвати не після, а до його розрізання. Потім вчитель показує цілий круг і його половину і говорить: це один круг, а це половина круга. Інакше говорять: одна друга частинам круга. Скільки других частин в крузі? – дві, покажіть їх.

Візьміть квадрат. Як одержати одну другу частину або половину квадрата? – поділити його на дві рівні частини і взяти одну таку частину. Виконуйте. Далі учням пропонуємо такі запитання: як одержати одну другу частину круга? Як одержати одну другу частину квадрата? Як можна назвати одну другу частину круга, квадрата? Скільки половинок круга в цілому крузі? Учні повинні накласти половинки круга на круг. Для того, щоб учні добре усвідомили поняття „частина величини”, корисно на першому уроці розглянути поділ і на нерівні частини, встановивши при цьому відмінності в цих способах поділу. Аналогічно розглядаються і інші частини величини. Слід пам’ятати лише про те, що у багатьох дітей уявлення про “другу частину”, “третю частину”, „четверту частину” тощо являє собою останню, другу, третю, четверту частину, а решту частин вони називають перша, друга, третя. Саме тому учням слід пояснити, що при поділі квадрата на 5 рівних частин, кожна із п’яти частин, є п’ята частина. Якщо учні помітять зв’язок між числом рівних частин і назвою кожної частини, то вони легко будуть знаходити сьому, дев’яту тощо, частини.

На третьому етапі вивчення теми, учні ознайомляться із записом частин за допомогою двох чисел. Ознайомлення із записами виду 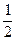, , , 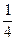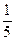тощо проводиться на конкретних прикладах без введення термінів „чисельник”, „знаменник”. Вчитель пояснює, якщо круг поділено на 4 рівні частини і потрібно позначити одну четверту частину, то проводять риску і під нею пишуть число 4, щоб показати, що це четверта частина числа. Над рискою пишуть число 1, щоб показати, що це одна така частина. При цьому учні повинні розуміти, що означає кожне число в записі , як одержати ? Аналіз системи вправ нині діючих підручників і методичних посібників для вчителів дозволяє зробити висновок про те, що для закріплення цих знань використовують такі вправи: 1) називання і запис частин; 2) зображення певних частин.

На четвертому етапі відбувається порівняння частин. Порівняння часток відбувається практично для однієї і тієї ж самої величини за допомогою наочних посібників. Так, наприклад, можна запропонувати учням накреслити 4 смужки довжиною 12 см. і зафарбувати 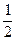, , 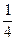їх частину. Діти переконуються, що найбільша 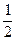, а найменша . Аналогічні вправи можна розглянути і з іншими предметами: кругами, квадратами тощо. У процесі закріплення корисно пропонувати учням запитання, які будуть готувати їх до вивчення дробів. Наприклад, розглядаючи малюнок можна запропонувати такі запитання: які частки прямокутника зафарбовані? Скільки таких частин не зафарбовано? Скільки і які частини не зафарбовано? Скільки четвертих частин в цілому крузі? У половині круга? Формування уявлень учнів про частини не обмежується уроками з даної теми, а продовжується при вивченні інших питань шляхом систематичного розв’язування вказаних вправ на наступних уроках. Щоб одержати дані про сформованість уявлень учнів про частини, вчитель повинен час від часу пропонувати учням давати відповіді на наступні запитання: як одержати половину яблука, круга, смужки, прямокутника, квадрата?

Яка ж методика ознайомлення дітей з частинами? – оскільки учні можуть мати певні уявлення про частини, то вчитель повинен виявити, уточнити (а при необхідності і виправити) та систематизувати наявні уявлення. З цією метою у кожного школяра повинен бути набір різноманітних кругів, прямокутників, квадратів, смужок тощо. Вчитель пропонує дітям вибрати серед наявних фігур дві однакові за розмірами, наприклад, два однакових круга. Після цього пропонуємо учням перегнути один із них так, щоб одержати рівні частини. Якщо діти не справляться з таким завданням самостійно, то вчитель демонструє як це робиться. Для кращого наочного підкріплення слід розрізати круг на дві частини по лінії згину та накладанням переконатися, що вони рівні та що у цілому крузі вміщується по дві таких частини.

Далі вчитель проводить бесіду. Які частини одержали? – рівні. Як би Ви назвали ці частини круга? – половинками. У математиці половинки круга називають другими частинами круга. Скільки в крузі половинок або других частин? – дві. Покажіть їх! Які ці частини? – рівні. Як у математиці називають такі частини? - однією другою частиною круга. Як одержати одну другу частину квадрата? – поділити його на дві рівні частини. Виберіть квадрат і одержіть одну другу частину квадрата!

Далі пропонуємо учням такі запитання: як одержати 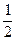частину круга? Як одержати 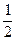частину квадрата? Як ще називають одну другу частину квадрата? круга? – половина. Скільки половин або других частин у квадраті? крузі? – дві. Які ці частини? – рівні. Для того, щоб перевірити чи правильні уявлення формуються у школярів, вчитель пропонує розглянути дітям малюнки №№ 13.7. і 13.8. та пропонує відповісти на наступні запитання: яка фігура зображена на малюнку 7? – прямокутник. На скільки частин його поділено? – на дві. Які ці частини? – рівні. Як би Ви назвали їх? – половиною або однією другою частиною прямокутника. Аналогічні запитання ставимо перед учнями, розглядаючи малюнок № 13.8. Відмінність полягатиме лише в тому, що вчителеві слід наголосити, що частини не рівні, а тому їх не можна назвати другими частинами прямокутника. Відповідь учнів повинна бути приблизно такою: їх не можна назвати другими частинами прямокутника, бо вони не рівні.

Поиск по сайту: