ТМО навчання учнів розв’язувати задачі на знаходження частини від числа, дробу від числа та числа за його частиною

3. Аналіз вимог програми з математики для І-ІУ класів і системи вправ нині діючих підручників з математики дозволяють зробити висновок про необхідність у зв’язку із вивченням тем „Частини величини” та „Дроби” формування в учнів уміння розв'язувати таких видів задач, пов’язаних з дробами: 1) задачі на знаходження частини числа, наприклад: “Від смужки паперу довжиною 12 см відрізали 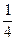її частину. Чому дорівнює довжина відрізаної частини смужки?”; 2) задачі на знаходження числа за його частиною, наприклад: “Сергійко відрізав від смужки 3 см. Це становить 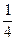довжини всієї смужки. Яка довжина всієї смужки?”; 3) задачі на знаходження дробу числа, наприклад: “У зошиті 24 сторінки. Дівчинка списала числа сторінок зошита. Скільки сторінок зошита списала дівчинка?”.

Таблиця № 13.11.

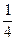
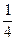
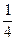
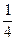
Відповідно до ТМО навчання школярів розв'язувати задачі формування цього уміння відбувається у процесі розв’язування простих, а потім і складених текстових задач. Спочатку розглядаються лише прості текстові задачі на знаходження частини числа та числа за його частиною, які пізніше розглядаються разом і включаються в складені. Задачі названих видів пропонуються як для усного, так і для письмового розв’язування. Експериментальні дослідження та практика роботи вчителів дозволяють твердити, що на перших етапах слід застосовувати наочність і обирати задачі з іменованими числами.

Розглянемо більш детально ТМО навчання учнів розв'язувати задачі на знаходження частини числа. Першою краще взяти задачу, яку легко проілюструвати (ця закономірність справджується при ознайомленні з двома іншими видами розглядуваних задач!). Наприклад: “Від смужки паперу довжиною 12 см відрізали 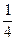її частину. Чому дорівнює довжина відрізаної частини смужки?”. Підготовчою роботою до ознайомлення школярів із задачами цього виду буде повторення відомостей про частини, що дозволить зняти зайві труднощі. Відповідно до індивідуально-психологічних особливостей учнів вчитель пропонує учням вирізати чи накреслити смужку довжиною 12см. Після цього діти практично виконують перегинання чи поділ смужки на чотири рівні частини з наступним відрізанням 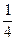частини. Практична робота супроводжується запитаннями вчителя: яка довжина всієї смужки? – 12 см. На скільки рівних частин ми її поділили? – на чотири. Довшою чи коротшою буде відрізана частини? – коротшою. У скільки разів? – у чотири. Якою дією знайдемо довжину відрізаної смужки? – дією ділення. Як запишемо розв’язання задачі? – 12:4=3 (см). При розв’язуванні наступних задач для більшості учнів достатньо використати лише малюнок (пропонуємо студентам виконати завдання № 32 для самостійної роботи).

Сутність ТМО навчання учнів розв'язувати задачі на знаходження числа за його частинами розглянемо на прикладі такої задачі “Сергійко відрізав від смужки паперу 3 см. Це становить 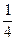довжини всієї смужки. Яка довжина всієї смужки?”. Пропонуємо учням зобразити смужку паперу, яку відрізав Сергійко, та відповісти на наступні запитання: яку частину вона складає від всієї смужки? – 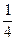. Скільки таких частин буде в усій смужці? – чотири. Як зобразити всю смужку? – домалювати ще три таких частини. У скільки разів довжина всієї смужки буде довшою за її 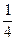частину? – у чотири. Як знайти довжину всієї смужки? – 3 см помножити на 4. Як запишемо розв’язання задачі? – 3●4=12 (см).

Розглянемо ТМО навчання учнів розв'язувати задачі на знаходження дробу числа на прикладі такої “У зошиті 24 сторінки. Дівчинка списала числа сторінок зошита. Скільки сторінок зошита списала дівчинка?”. Враховуючи індивідуальні особливості учнів і особливості їхнього мислення, використаємо наочне підкріплення. Це сприятиме особистісній орієнтації навчального процесу. Зобразимо загальну кількість сторінок зошита клітинками, прийнявши одну клітинку за одну сторінку. Скільки клітинок зошита слід обвести, якщо у зошиті 24 сторінки? – 24. Яку частину сторінок зошита списала дівчинка? – . Як зобразити списані сторінки? – зафарбувати чи закреслити. Що означає дріб ? – що 24 сторінки поділили на 8 рівних частин і взяли 5 таких частин. Що визначимо, коли 24:8? – скільки сторінок складає частина. Як визначити скільки сторінок складає ? – необхідно кількість сторінок, що складають , помножити на 3. Чи дамо ми вже тепер відповідь на запитання задачі? – так. Розв’язання таких задач записують так: 24:8●5=15 (ст.). Формування уміння розв'язувати задачі вказаних видів відбувається спочатку при розв’язуванні простих задач. Вказані міркування діти повинні поступово привчатися проводити самостійно. Дещо пізніше включають складені задачі, в яких вказані вище три види є простими. З метою формування відповідних умінь пропонуємо студентам виконати завдання № 33 для самостійної роботи.

Поиск по сайту: