 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Влияние факторов ОРМ на стоимость колл опциона
| Вариант | Фактор | |||||
| P, дол. | X, дол. | t, лет |  ,% ,%
| 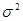
| V, дол. | |
Базовый
Увеличение Р на 5 дол. Увеличение X на 5 дол. Увеличение t до 6 мес. Увеличение  до 16% Увеличение до 16% Увеличение 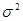 до 0.25 до 0.25
| 20 >25 | 0.25 0.25 0.25 0.50 0.25 0.25 | 0.16 0.16 0.16 0.16 0.16 0.25 | 1.88 5.81 0.39 2.81 1.99 2.27 |
Таким образом, стоимость опциона при принятых условиях равняется 1.88 дол. Предположим, что фактическая цена опциона была бы 2.25 дол. Арбитражеры могли бы одновременно продать опцион и купить базисную акцию и тем самым заработать безрисковую прибыль. Такая торговля приводила бы к тому, что цена опциона стремилась бы к 1.88 дол. Обратное имело бы место, если бы опцион продавался за цену, меньшую чем 1.88 дол. Таким образом, инвесторы не склонны платить больше 1.88 дол. за опцион, но и не могут покупать его за меньшую цену, поэтому 1.88 дол. является равновесной стоимостью (equilibrium value) опциона.
Чтобы понять, как каждый из пяти факторов ОРМ влияет на стоимость опциона, V, рассмотрим табл. 5.2. Верхняя строка таблицы показывает исходные данные и результирующую цену опциона — V — 1.88 дол. Исходные данные — те же самые, которые ранее мы использовали для иллюстрации модели. В каждой последующей строке один фактор является возрастающим, тогда как величины других четырех остаются постоянными на их первоначальном уровне. Результирующая стоимость колл опциона приводится в последней графе. Рассмотрим влияние каждого из этих факторов.
1. Текущая цена акции. Когда текущая цена акции, Р, возрастает с 20 до 25 дол., стоимость опциона возрастает с 1.88 до 5.81 дол. Таким образом, стоимость опциона возрастает с ростом цены акции, но с меньшим темпом: 3.93 дол. по сравнению с 5.00 дол. Отметим тем не менее, что в процентном отношении увеличение стоимости опциона составляет (5.81 дол. — 1.88 дол.): 1.88 дол. = 209%, что намного превышает прирост цены акции (25 дол. — 20 дол.): 20 дол. = 25%.
2. Цена исполнения. Когда цена исполнения, X, возрастает с 20 до 25 дол., стоимость опциона снижается. Вновь заметим, что хотя абсолютное изменение стоимости опциона меньше, чем абсолютное изменение цены исполнения, но темп изменения стоимости опциона ((0.39 дол. —1.88 дол.): 1.88 дол. = —79%) превышает темп изменения цены исполнения.
3. Период действия опциона. Когда срок действия опциона возрастает с t = 3 месяца (или 0.25 года) до t = 6 месяцам (или 0.50 года), стоимость опциона возрастает с 1.88 до 2.81 дол. Этот результат возникает от того, что стоимость опциона зависит от возможности возрастания цены базисной акции, и чем дольше срок действия опциона, тем выше вероятность резкого роста цены акции. Таким образом, если остальные факторы остаются неизменными, 6-месячный опцион будет стоить дороже, чем 3-месячный.
4. Безрисковая процентная ставка. Следующий фактор — безрисковая процентная ставка,  . С увеличением процентной ставки с 12 до 16% стоимость опциона возрастает незначительно, с 1.88 до 1.99 дол. Формулы (5.2)—(5.4) предполагают, что главный эффект от возрастания f
. С увеличением процентной ставки с 12 до 16% стоимость опциона возрастает незначительно, с 1.88 до 1.99 дол. Формулы (5.2)—(5.4) предполагают, что главный эффект от возрастания f  заключается в усилении дисконтирования цены исполнения X ехр(—
заключается в усилении дисконтирования цены исполнения X ехр(—  t], что в свою очередь увеличивает текущую стоимость опциона.8 Безрисковая ставка также играет роль в определении величин функций нормального распределения N(d1) и N(d2), но это влияние имеет второстепенное значение. Действительно, цены опционов в целом не очень чувствительны к изменениям процентных ставок, по крайней мере в случае их нормального распределения.
t], что в свою очередь увеличивает текущую стоимость опциона.8 Безрисковая ставка также играет роль в определении величин функций нормального распределения N(d1) и N(d2), но это влияние имеет второстепенное значение. Действительно, цены опционов в целом не очень чувствительны к изменениям процентных ставок, по крайней мере в случае их нормального распределения.
5. Вариация цены базисного актива. С увеличением вариации с 0.16 до 0.25 стоимость опциона возрастает с 1.88 до 2.27 дол. Таким образом, чем более рисковой является базисная ценная бумага, тем большую стоимость будет иметь опцион. Этот результат логичен. Во-первых, если вы приобрели опцион, чтобы купить акцию, которая продается по своей цене исполнения, и если 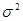 = 0, это означает, что существует нулевая вероятность того, что цена акции поднимется и, следовательно, опцион не принесет дохода. С другой стороны, если бы вы купили опцион на акции с высоким уровнем разброса цен, то ясно — существует большая вероятность того, что акции возрастут в цене, т. е. опцион может принести большую прибыль. Конечно, цена акции с высоким уровнем разброса цен может снизиться, однако в этом случае, поскольку вы являетесь держателем опциона, ваши убытки ограничены ценой, уплаченной за его покупку. С другой стороны, возможный значительный доход от возрастания акции в цене более привлекателен, чем возможный ограниченный убыток от снижения цен, поэтому чем больше вариация, тем больше стоимость опциона. Все это делает опцион на рисковые акции более дорогим по сравнению с устойчивыми акциями с малой вариацией доходов.
= 0, это означает, что существует нулевая вероятность того, что цена акции поднимется и, следовательно, опцион не принесет дохода. С другой стороны, если бы вы купили опцион на акции с высоким уровнем разброса цен, то ясно — существует большая вероятность того, что акции возрастут в цене, т. е. опцион может принести большую прибыль. Конечно, цена акции с высоким уровнем разброса цен может снизиться, однако в этом случае, поскольку вы являетесь держателем опциона, ваши убытки ограничены ценой, уплаченной за его покупку. С другой стороны, возможный значительный доход от возрастания акции в цене более привлекателен, чем возможный ограниченный убыток от снижения цен, поэтому чем больше вариация, тем больше стоимость опциона. Все это делает опцион на рисковые акции более дорогим по сравнению с устойчивыми акциями с малой вариацией доходов.
На этом заканчивается обсуждение природы опционов и теории их ценообразования. В следующем разделе будет показано, как можно использовать теорию ценообразования опционов с целью принятия решений по финансовому менеджменту.
Вопросы для самопроверки
Какова цель ОРМ?
Объясните, что такое безрисковый хедж и как концепция безрискового хеджа используется в модели ОРМ.
Объясните, каким образом нижеперечисленные факторы воздействуют на цену колл опциона: 1) цена акции, 2) цена исполнения, 3) период опциона, 4) безрисковая ставка, 5) вариация цены акции.
Ценообразование опционов и корпоративная финансовая политика
Собственный капитал финансово зависимой фирмы может рассматриваться как колл опцион: когда фирма эмитирует долговые обязательства, это по смыслу эквивалентно тому, что акционеры продают активы фирмы кредиторам, которые платят за активы наличностью, и, с другой стороны, также дают акционерам подразумеваемый колл опцион с ценой исполнения, равной стоимости основного долга плюс процент. Если деятельность компании успешна, акционеры будут «выкупать компанию обратно» исполнением своих колл опционов, которые означают погашение суммы долга и выплату процентов. Если деятельность компании не является успешной, акционеры не погасят ссуду, что приведет к неисполнению их колл опциона и, следовательно, переходу компании в руки кредиторов.
В качестве иллюстрации предположим, что корпорация «One Shot» как раз собирается осуществлять одногодичные инвестиции в фирму, производящую пуговицы для кандидатов в президенты. Фирма требует инвестиций в размере 10000 дол., из которых 7500 дол. должны быть получены путем продажи долговых обязательств с процентной ставкой 10%, а другие 2500 дол. должны быть собраны в результате эмиссии обыкновенных акций. Распределение доходов между держателями долговых обязательств и акционерами предполагается сделать в конце года. По истечении года стоимость фирмы будет зависеть прежде всего от того, какие кандидаты успешно пройдут первичные выборы, а также в некоторой степени от положения на рынке коллекционеров. Пусть имеется следующее вероятностное распределение стоимости фирмы.
| Вероятность...... | 0.7 | 0.2 | 0.1 |
| Стоимость, дол.... |
Таким образом, ожидаемая стоимость фирмы в конце года есть 0.7 * 20000 дол. + 0.2 * 5000 дол. +0.1*0 дол. = 15000 дол.
Если прогнозы акционеров верны, то, сделав инвестицию в размере 2500 дол., они по окончании года получат прибыль до налогообложения в размере 6750 дол. (в дол.):
| Ожидаемая стоимость........... | |
| Кредиторская задолженность... | — 7500 |
| Проценты за кредит............. | — 750 |
| Доход до налогообложения....... |
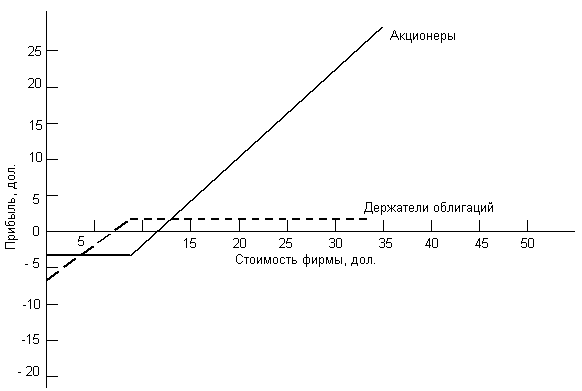
Рис. 5.6. Графики выплат для акционеров и держателей облигаций.
Однако ожидаемая стоимость не является достижимой. Стоимость фирмы будет либо 0 дол., либо 5000 дол., либо 20000 дол. Если стоимость окажется 0 дол. либо 5000 дол., то акционеры не исполнят свой опцион, вместо этого они прекратят платежи. Держатели долговых обязательств тогда будут вправе продать фирму, и акционеры ничего не получат. Однако, если стоимость фирмы достигнет величины 20000 дол., акционеры исполнят свой опцион, уплатив держателям облигаций 8250 дол. и оставив в своем распоряжении 11 750 дол. (до налогообложения). Таким образом, владение акциями может рассматриваться как колл опцион. В этом примере инвестиции в акции в размере 2500 дол. (текущая цена колл опциона) дают право акционерам выкупить активы фирмы у держателей долговых обязательств за 8250 дол. (цена исполнения).
Сплошная линия на рис. 5.6 описывает доходы акционеров. Предполагается, что ожидаемая стоимость фирмы меняется непрерывно, не ограничиваясь упомянутыми в примере тремя значениями. Если стоимость фирмы будет меньше чем 8250 дол. (цена исполнения колл опциона), акционеры потеряют свои первоначальные инвестиции в 2500 дол. При стоимости выше 8250 дол. акционеры исполнят свой опцион, расплатятся с держателями облигаций, оставив в своем распоряжении весь капитал сверх цены исполнения. Таким образом, график акционера на рис. 5.6 имеет ту же самую форму, что и график держателя колл опциона на рис. 5.1.
Аналогичным образом можно оценить позицию держателей облигаций. Если стоимость фирмы становится меньше чем 8250 дол., ее активы будут полностью принадлежать держателям облигаций, поскольку акционеры не исполнят свой опцион на фирму. Однако держатели облигаций не будут иметь прибыли до тех пор, пока стоимость фирмы не достигнет 7500 дол. Каждый доллар превышающий эту величину, т. е. из интервала 7500-8250 дол., будет представлять собой прибыль держателей облигаций, а общая ее величина составит 750 дол. процентных платежей. Акционеры, исполнив свой опцион, получат в свое распоряжение стоимость, превышающую 8250 дол. Прерывистая линия на рис. 5.6 иллюстрирует доходы держателей облигаций. Сравнивая график доходов держателей облигаций с графиком на рис. 5.2, мы замечаем, что доходы держателей долговых обязательств совпадают по форме с доходами продавца пут опциона. Однако для понимания логики процесса нагляднее рассуждать в рамках идеологии колл опциона. В этом случае позиция держателей облигаций может быть описана как: 1) владение фирмой и 2) продажа колл опциона на стоимость фирмы с ценой исполнения 8250 дол.
Во многих журнальных статьях теория опционов применялась к инвестициям в акции и облигации, и на многие вопросы теории корпоративных финансов уже имеются новые точки зрения.9 Далее мы рассмотрим два вопроса по теории корпоративных финансов, а также проанализируем в главе 24 возможность применения теории опционов для слияния компаний.
Инвестиционные решения
Предположим, что фирма, привлекающая заемные средства, имеет крупный портфель казначейских векселей. Управляющие фирмы могли бы продать векселя (которые являются безрисковыми) и использовать выручку для покупки рисковых активов, которые увеличили бы вариацию доходов фирмы, не воздействуя при этом на систематический риск фирмы. Так как капитал фирмы можно рассматривать как колл опцион, возрастающая вариация увеличила бы рыночную стоимость без увеличения ее рыночного риска. Риск банкротства возрос бы, но акционеры увеличили бы шансы получения больших прибылей при одновременном ограничении убытков суммой своих инвестиций.
Необходимо отметить, что некоторое увеличение прибыли может быть получено акционерами за счет держателей долговых обязательств. Для иллюстрации предположим, что первоначальная стоимость активов фирмы была 4 млн дол. и фирма имела на 2 млн дол. кредиторской задолженности со сроком погашения через два года. (Процент, который будет выплачен в конце срока, включен в балансовую стоимость долга, поэтому долг является дисконтированной величиной). Далее предположим, что вариация доходности активов фирмы, 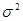 , равняется 0.01 и безрисковая ставка — 10%. Если мы будем рассматривать акции как колл опцион на активы фирмы, то в формулах (5.2) и (5.3) будем иметь: V — текущая стоимость колл опциона, или текущая рыночная оценка акционерного капитала; Р — текущая стоимость фирмы, или 4 млн дол.; X — цена исполнения, или балансовая стоимость долга в размере 2 млн дол.
, равняется 0.01 и безрисковая ставка — 10%. Если мы будем рассматривать акции как колл опцион на активы фирмы, то в формулах (5.2) и (5.3) будем иметь: V — текущая стоимость колл опциона, или текущая рыночная оценка акционерного капитала; Р — текущая стоимость фирмы, или 4 млн дол.; X — цена исполнения, или балансовая стоимость долга в размере 2 млн дол.
Используя формулы (5.2)—(5.4), находим, что искомая рыночная стоимость акций фирмы должна равняться 2362538 дол.:
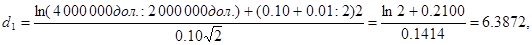
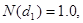
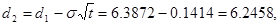
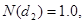
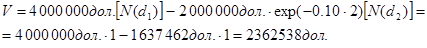
Если стоимость фирмы равняется 4 млн дол. и рыночная оценка акционерного капитала, найденная с помощью ОРМ, составляет 2 362 538 дол., то предполагаемая рыночная оценка (или приведенная стоимость) балансовой стоимости долга в 2 млн дол. должна быть 1637462 дол.
Теперь предположим, что фирма использует некоторые из своих ликвидных активов на покупку рисковых активов, увеличивая отклонение значения доходности с 0.01 до 0.10. Таким образом, в новой ситуации 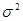 = 0.10 и
= 0.10 и 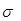 = 0.3162. Вновь вычислим рыночные оценки акционерного и заемного капитала, предполагая, что стоимость фирмы остается неизменной в размере 4 млн. дол.:
= 0.3162. Вновь вычислим рыночные оценки акционерного и заемного капитала, предполагая, что стоимость фирмы остается неизменной в размере 4 млн. дол.:
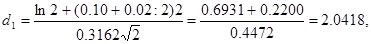
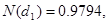
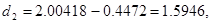
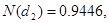
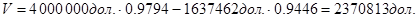
Предполагаемая рыночная оценка заемного капитала сейчас составляет 4000000 дол. - 2370813 дол. = 1629187 дол. Таким образом, в условиях предпосылок ОРМ и САРМ, которые должны быть приняты во внимание, и допущения о неизменности оценки фирмы ее акционеры в результате описанной операции получат прибыль 2370813 дол. - 2362538 дол. = 8275 дол. за счет средств держателей долговых обязательств. Этот пример показывает, как велико значение ограничительных соглашений, которые держатели долговых обязательств могут использовать, чтобы защитить себя от возможных действий акционеров, способных сократить рыночную оценку заемного капитала.
Решения о структуре капитала
Предположим, что фирма планирует удвоить свою долгосрочную кредиторскую задолженность с тем, чтобы использовать полученные средства для выкупа собственных акций. Активы фирмы при этом не изменятся. Возрастани левериджа, характеризующего степень финансовой зависимости фирмы, приведет к увеличению вариации чистого дохода фирмы и соответственно к росту вариации рыночной оценки собственного капитала. При прочих равных условиях это приведет к увеличению стоимости акций, поскольку акционеры имеют колл опцион на стоимость фирмы. Численный анализ может быть выполнен по той же схеме, что и в предыдущем примере. Ясно, что дополнительный долг поставил бы держателей долговых обязательств в более рисковую позицию. В результате рыночная оценка долга упала бы и это снижение было бы равно прибыли акционеров.
Вопросы для самопроверки
Опишите, в каком смысле акции финансово зависимых фирм могут рассматриваться как колл опционы.
Что говорит теория ценообразования опционов о том, как изменения в активах могут влиять на стоимость долговых обязательств и акций фирмы?
Что говорит теория ценообразования опционов о том, как изменения в структуре капитала могут влиять на рыночную оценку долговых обязательств и акций фирмы?
Заключительные замечания о теории опционов
Понятие опциона является важным элементом теории инвестиций, поэтому студентам, изучающим эту область, необходимо иметь знания о том, как опционы используются и оцениваются на рынке. Далее, теория опционов помогает нам понимать природу сходных с опционами ценных бумаг, таких как варранты и конвертируемые ценные бумаги. Однако роль теории опционов в принятии решений по финансовому менеджменту менее ясна. Как мы видели, можно использовать теорию опционов для понимания роли инвестиционных решений в отношении стоимости долговых обязательств и акций фирмы. Однако эти вопросы на самом деле достаточно очевидны, и можно представить себе последствия изменений в рисковых активах даже не прибегая к помощи ОРМ, а лишь основываясь на общих рассуждениях. Опционный анализ в целом делается в предположении «о неизменности прочих условий», хотя очевидно, что другие параметры редко сохраняются неизменными, когда фирмы делают существенные изменения в своих активах и/или структуре капитала. Тем не менее не исключено, что подход ОРМ может в будущем привести к более точным количественным оценкам определенных эффектов, которые могли бы быть полезны в структурировании контрактов и принятии других решений финансового характера. В главе 8 будет показано, как ОРМ используется в некоторых компаниях для оценки управленческих опционов, являющихся составной частью инвестиционной политики. В любом случае теория ценообразования опционов может сыграть огромную роль в принятии решений по финансовому менеджменту в будущем, поэтому студенты, изучающие корпоративные финансы, должны быть осведомлены о разработках в этой области.
Резюме
В этой главе были рассмотрены природа опционов и основы теории ценообразования опционов. Было показано, как эта теория может быть применима к оценке влияния различных управленческих решений на доходы акционеров и кредиторов. Перечень ключевых концепций приводится ниже.
• Опционы — финансовые инструменты, которые: 1) чаще создаются биржами, а не фирмами, 2) покупаются и продаются преимущественно инвесторами, 3) представляют большее значение для инвесторов, нежели для финансовых менеджеров.
• Знакомство с теорией опционов необходимо финансовым менеджерам для понимания природы варрантов и конвертируемых ценных бумаг, являющихся по сути инструментами типа опционов (мы будем обсуждать это в главе 16).
• Концепция опционов полезна также в некоторых ситуациях, связанных с планированием бюджета капиталовложений (мы будем обсуждать это в главе 8).
• Колл опцион дает держателю право купить базисный актив по определенной цене (цене исполнения) в течение данного периода.
• Пут опцион дает держателю право продать базисный актив по определенной цене в течение данного периода.
• Цена опциона — сумма, уплачиваемая покупателем опциона продавцу.
• Дата истечения опциона — последний день, в который опцион может быть исполнен.
• Европейские опционы могут быть исполнены только в день истечения опциона, тогда как американские — в любое время до наступления даты истечения опциона, включая саму дату.
• Если продавец колл опциона на акции владеет базисными активами, то говорят, что он продает покрытый колл опцион. Наоборот, если продавец не владеет базисными акциями, колл опцион считается непокрытым.
• Если цена на базисные акции выше цены исполнения колл опциона, то говорят, что опцион находится «в деньгах». Если цена акции ниже цены исполнения, то говорят, что опцион находится «без денег». Пут опционы имеют противоположные определения.
• График выплат позволяет наглядно увидеть доходы по опциону в момент истечения опциона.
• Пут—колл паритет демонстрирует, что цены колл и пут опционов на одни и те же акции с одной и той же ценой исполнения зависят друг от друга. Если зависимость между ценами опционов на рынке значительно отличается от паритетной, инвесторы могут получать дополнительные доходы конструированием позиций, представляющих собой комбинации пут и колл опционов. 3aнятие таких позиций постепенно приведет к установлению пут—колл паритета.
• В течение периода действия опциона рыночная цена колл опциона больше, чем его внутренняя стоимость, потому что всегда есть шанс, что к моменту истечения срока опциона цена на базисные акции поднимется выше ее текущего уровня.
• Модель ценообразования опционов Влэка—Шоулза (ОРМ) может быть использована для оценки стоимости колл опциона.
• Стоимость колл опциона является функцией пяти переменных: 1) текущей цены акции, 2) цены исполнения, 3) периода опциона, 4) безрисковой ставки, 5) вариации цены акции.
• Как собственный, так и заемный капитал фирмы могут рассматривается в рамках теории опционов. Имея это в виду, можно получить представление о влиянии изменений в активах и источниках средств на рыночную оценку долговых обязательств и акционерного капитала.
Вопросы
5.1. Дайте определение следующих понятий:
а) опцион;
б) колл опцион;
в) пут опцион;
г) цена исполнения;
д) цена опциона;
е) дата истечения опциона;
ж) внутренняя стоимость;
з) европейский опцион;
и) американский опцион;
к) покрытый колл опцион;
л) опцион «в деньгах»;
м) опцион «без денег»;
н) график выплат;
о) пут—колл паритет.
5.2. Почему опцион продается обычно по цене, превышающей его внутреннюю стоимость?
5.3. Каким образом каждый из перечисленных ниже факторов влияет на цену колл опциона?
а) текущая цена базисного актива;
б) цена исполнения;
в) дата истечения опциона;
г) безрисковая ставка;
д) вариация цены базисного актива.
5.4. Почему инвесторы нередко составляют комбинации различных опционных контрактов?
5.5. Что такое длинный стрэддл? При каких условиях инвестор будет конструировать длинный стрэддл?
5.6. На какую связь между колл и пут опционами указывает пут—колл паритет?
5.7. Какие предпосылки заложены в основу модели Блэка—Шоулза?
5.8. Поясните, почему обыкновенные акции финансово зависимой фирмы можно трактовать как колл опцион?
5.9. Используя теорию ценообразования опционов, поясните, что происходит с оценкой акционерного и долгосрочного заемного капитала в случае, когда фирма меняет структуру активов, повышая долю относительно более рисковых активов.
Задачи
5.1. График выплат и пут—колл паритет. Имеются следующие данные о компании «Data Systems, Inc.»:
| Текущая цена акций... | 50 дол. |
| Цена исполнения....... | 45 дол. |
| Цена пут опциона....... | 1 дол. |
| Безрисковая ставка..... | 6.0% |
а. Постройте график выплат для пут опциона.
б. Используя формулу пут—колл паритета, оцените одногодичный колл опцион этой же компании с ценой исполнения 45 дол. (Предполагается, что в течение года фирма не выплачивает дивиденды по акциям и опционы европейские).
5.2. График выплат и пут—колл паритет. Имеются следующие данные о компании «Biotechmatics»:
| Текущая цена акций... | 25 дол. |
| Цена исполнения....... | 30 дол. |
| Цена пут опциона....... | 6 дол. |
| Безрисковая ставка..... | 6.0% |
а. Постройте график выплат для колл опциона.
б. Используя формулу пут—колл паритета, оцените одногодичный пут опцион этой компании с ценой исполнения 30 дол. (Предполагается, что в течение года фирма не выплачивает дивиденды по акциям и опционы европейские).
5.3. Оценка в ситуации с двумя исходами. Текущая цена акций «Radcliffe Enterprises» равна 60 дол. По истечении года возможна одна из двух ситуаций: а) в случае успешной деятельности компании цена ее акций возрастет до 80 дол.; б) при неблагоприятных условиях цена может упасть до 40 дол. Акции компании продаются на рынке опционов, причем цена одногодичного колл опциона с ценой исполнения 60 дол. равна 10.23 дол. Чему равна одногодичная безрисковая ставка? (Указание: сконструируйте безрисковый хедж покупкой доли акции и продажей колл опциона).
5.4. Оценка в ситуации с двумя исходами. Рассмотрите пример безрискового портфеля с двумя исходами, приведенный в разделе «Введение в ценообразование опционов». В этом примере для конструирования безрискового портфеля была осуществлена покупка акций и продажа колл опциона.
а. Используя те же данные, постройте безрисковый портфель путем покупки части акции и пут опциона.
б. Полагая, что одногодичная безрисковая ставка равна 6%, найдите цену опциона.
5.5. Модель Блэка—Шоулза. Опционы компании «Cotner Software» (CSC) активно продаются на одной из региональных бирж. Текущая цена акций компании равна 10 дол., вариация доходности — 0.16. Текущая полугодовая безрисковая ставка равна 12%.
а. Используя модель Блэка—Шоулза, рассчитайте цену полугодового опциона с ценой исполнения 10 дол.
б. Как изменится цена опциона, если CSC реструктурирует свои активы, благодаря чему вариация доходов снизится до 0.09?
(Пункты «в» и «г» делайте с помощью электронных таблиц).
в. Предположим, что CSC вернулась к своей первоначальной структуре активов, т.е. вариация доходности — 0.16. Если текущая цена акций компании повысится до 15 дол., как это повлияет на цену опциона?
г. Рассчитайте цену опциона в условиях пункта «а», полагая, что цена исполнения равна 15 дол.
Мини-ситуация
«General Synergistics» (GS) является лидером на рынке биоинженерных технологий. Поскольку акции этой компании пользуются большим спросом среди инвесторов, пут и колл опционы GS с недавних пор стали продаваться на Чикагской опционной бирже. Старший управленческий персонал GS проявляет живой интерес к этому событию, однако лишь немногие из них понимают природу опционов и механизм их действия.
Являясь финансовым директором GS, Рекс Монкриф планирует организовать семинар на тему «Теория опционов и их оценка». Он просит вас, как только что нанятого фирмой опытного финансового аналитика, провести этот семинар. Р. Монкриф сформулировал следующие вопросы, на которые вам и нужно попытаться дать ответ.
1. Что такое опцион? Сформулируйте одну, но самую важную характеристику опциона.
2. В теории опционов применяется специальная терминология. Дайте определения понятий, приведенных в пункте 5.1 раздела «Вопросы».
3. Предположим, что на бирже продаются полугодовые пут и колл опционы GS с ценой исполнения 25 дол., тогда как текущая цена акции 27 дол. Цена колл опциона - 4 дол., цена пут опциона — 2 дол.
а. Какое минимальное число акций включается в опционный контракт?
б. Является ли колл опцион опционом «в деньгах»?
в. Что такое график выплат? Начертите его для пут и колл опционов компании GS
г. Что такое комбинация опционов? С помощью пут и колл опционов постройте пример длинного стрэддла. При каких экономических условиях инвесторы конструируют длинные стрэддлы?
4. В дальнейшем используйте следующие обозначения:
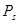 — цена акции в момент истечения опциона; Рр — цена пут опциона; Рх — цена исполнения; Рс — цена колл опциона;
— цена акции в момент истечения опциона; Рр — цена пут опциона; Рх — цена исполнения; Рс — цена колл опциона;  — безрисковая ставка; t — время до истечения опциона.
— безрисковая ставка; t — время до истечения опциона.
а. Постройте таблицу, характеризующую доходы от торговой стратегии, подразумевающей (цена исполнения во всех случаях одинакова): покупку базисного актива; продажу колл опциона; покупку пут опциона. При построении таблицы рассмотрите две ситуации, когда цена акции в момент истечения опциона меньше (больше) цены исполнения. Какова величина дохода в каждом случае? (Расходами по конструированию позиции пренебречь).
б. Используя имеющуюся информацию, постройте отношение пут—колл паритета.
в. Почему поддерживается пут—колл паритет? Что говорит это отношение о ценах на пут и колл опционы при условии, что цена исполнения в них одинакова?
4. Рассмотрим колл опцион GS с ценой исполнения 25 дол. Ниже приведены статистические данные о ценах на этот опцион при различных ценах базисного актива (в дол.):
| Цена акции....…… | ||||||
| Цена опциона ….. | 3.00 | 7.50 | 12.00 | 16.50 | 21.00 | 25.50 |
а. Составьте таблицу, показывающую: цену акции; цену исполнения; внутреннюю стоимость; цену опциона; премию как превышение цены опциона над внутренней стоимостью.
б. Что происходит с премией, если цена акции повышается? Поясните.
6. В 1973 г. Ф. Блэк и М. Шоулз создали свою модель оценки опционов (ОРМ).
а. Какие предпосылки заложены в модель?
6. Распишите три формулы, входящие в модель.
в. Рассчитайте цену опциона по следующим данным:
| Цена акции................... | 27 дол. |
| Цена исполнения.............. | 25 дол. |
| Период истечения опциона.... | 6 месяцев |
| Безрисковая ставка........... | 6.0% |
| Вариация доходности акции... | 0.11 |
7. Какое влияние оказывают на цену опциона следующие параметры:
а) текущая цена акции;
б) цена исполнения;
в) дата истечения опциона;
г) безрисковая ставка;
д) вариация доходности базисного актива.
8.а. Поясните, почему собственный капитал финансово зависимой компании можно трактовать как колл опцион.
б. Предположим, что GS существенно повысила общий риск своих активов путем изменения их структуры, не повлияв тем самым на рыночный риск акций. Какой эффект будет иметь эта акция в отношении акционеров и держателей долговых обязательств в соответствии с теорией ценообразования опционов?
в. Предположим, что компания удвоила величину долгосрочной кредиторской задолженности. В соответствии с теорией ценообразования опционов — какой эффект будет иметь эта акция в отношении акционеров и держателей долговых обязательств?
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
Некоторые аспекты теории опционов изложены в литературе по проблемам инвестиций (см. главу 2). Кроме того, можно использовать следующие работы:
Сох J. С., Rubinstein М. Options Markets. Englewood Cliffs, N. J.: Prentice-Hall, 1985.
Hull J. Options, Futures, and Other Derivative Securities. Englewood Cliffs, N. J.: Prentice-Hall, 1989.
Strong R. A. Speculative Markets: Options, Futures, and Hard Assets. Chicago: Deardorn, 1989.
В оригинальной статье Блэка и Шоулза рассмотрена адекватность прогнозных з рактеристик ОРМ фактическим рыночным ценам. Дополнительные работы по провер этой модели:
Galai D. Tests of Market Efficiency of the Chicago Board Options Exchange // Journ. Business. 1977. Apr. P. 167-197.
Gultekin N. В., Rogalski R. J., Tinic S. M. Option Pricing Model Estimates: Some Empirical Results // Financial Management. 1982. Spring. P. 58-69.
MacBeth J. D., Merville L. J. An Empirical Examination of the Black—Scholes Call Option Pricing Model // Journ. Finance. 1979. Dec. P. 1173-1186.
Ниже приведен ряд примечательных статей по теории опционов:
Black F. Fact and Fantasy in the Use of Options and Corporate Liabilities // Financial Analysts Journ. 1975. July—Aug. P. 36-41, 61-72.
Figlewski S. Options Arbitrage in Imperfect Markets // Journ. Finance. 1990. Dec. P. 1289 - 1311.
Frankfurter G. M., Leung W. K. Further Analysis of the Put—Call Parity Implied Risk-Free Interest Rate // Journ. Financial Research. 1991. Fail. P. 217-232.
Geske R., Roll R. On Valuing American Call Options with the Black—Scholes European Formula // Journ. Finance. 1984. June. P. 443-455.
Longstaff F. A. Pricing Options with Extendible Maturities: Analysis and Applications // Ibid. 1990. July. P. 935-957.
Vijh A. M. Liquidity of the СВОЕ Equity Options // Ibid. 1990. July. P. 1157-1179.
Whalcy R. E. Valuation of American Call Options on Dividend Paying Stocks: Empirical Tests // Journ. Financial Econ. 1982. March. P. 29-58.
Поиск по сайту: