 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Кривые безразличия риск—доходность
Какой конкретный портфель следует выбрать инвестору из всего эффективного множества портфелей? Для того чтобы определить портфель, оптимальный с точки зрения отдельного инвестора, нужно знать его отношение к риску, проявляющееся в выборе параметров функции, описывающей взаимосвязь между риском и доходностью и называемой кривой безразличия (indifference curve).
В основе построения этой функции заложены стандартные экономические концепции теории полезности и кривых безразличия, примеры которых приведены на рис. 2.9. Кривые IY и IZ — это кривые безразличия инвесторов Y и Z. По мнению м-с Y, портфель с ожидаемым уровнем доходности в 5% является безрисковым, портфелю с ожидаемым уровнем доходности в 6% уже присущ риск в размере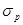 
= 1.4%, и т. д. М-р Z также считает безрисковым портфель с уровнем доходности в 5%, рисковость портфеля с уровнем доходности в 6% он оценивает величиной 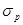= 3.3%, и т. д.
Отметим, что м-с Y требуется более высокая ожидаемая доходность в качестве компенсации за определенный уровень риска; таким образом, можно сказать, что м-с Y менее склонна к риску, чем м-р Z. Ее менее высокая склонность к риску приводит к тому, что по сравнению с м-ром Z м-с Y требует более высокую премию за риск, которая в данном случае определяется как разность между 5%-ным уровнем безрисковой доходности и ожидаемой доходностью, требуемой для того, чтобы компенсировать определенный уровень риска. Например, м-с Y требуется прирост доходности в размере 2.5% в качестве компенсации за риск 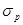= 3.3%, тогда как премия м-ра Z за данный уровень риска составляет лишь RPZ = 1-0%. Если говорить в целом, то чем круче наклон кривой безразличия, тем в меньшей степени инвестор склонен к риску.
Каждому индивидууму соответствует целая «карта» кривых безразличия; соответствующие карты м-с Y и м-ра Z приведены на рис. 2.10. Более высокий уровень кривой безразличия означает более высокий уровень удовлетворенности (или полезности). Так, кривая 
лучше, чем кривая 
,т. е. для любого уровня риска ожидаемая доходность м-ра Z выше, следовательно, выше и полезность. Для каждого индивидуума можно построить бесконечное множество кривых безразличия, причем оно будет иметь сугубо индивидуальный характер.
Поиск по сайту: