Выбор оптимального портфеля

Как показано на рис. 2.6, в, допустимое множество портфелей, состоящих голько из двух активов, представляет собой прямую или кривую. При увели­чении числа активов линия трансформируется в некоторую область, например показанную на рис. 2.8. Точки А, Н, G и Е соответствуют отдельным цен­ным бумагам (или портфелям, состоящим только из одной ценной бумаги). Все остальные точки заштрихованной области, включая ее границы, соответствуют портфелям, состоящим из двух или более акций. Эта область называется допу­стимым, или возможным, множеством. Каждая точка области соответствует портфелю с риском 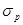и ожи­даемой доходностью 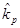. Например, координаты точки X — это значения риска и доходности одного из таких портфелей. То же можно утверждать и про точки В, С и D.

Множество потенциальных порт­фелей, которые можно составить из имеющихся на рынке активов, ве­лико. Естественно, возникает задача составления оптимального портфеля. Процедура такого выбора основыва­ется на двух независимых решениях: 1) определение эффективного множе­ства портфелей и 2) выбор из этого эф­фективного множества единственного портфеля, который является наилуч­шим для отдельного инвестора.

Поиск по сайту: