 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Теория арбитражного ценообразования
САРМ представляет собой однофакторную модель. Это означает, что риск является функцией одного фактора — ß - коэффициента, выражающего зависимость между доходностью ценной бумаги и доходностью рынка. Возможно, зависимость между риском и доходностью более сложная. В этом случае можно предположить, что требуемая доходность акции будет функцией более чем одного фактора. Например, не исключено, что инвесторы могут отдавать приоритет капитализированному доходу перед дивидендами, поскольку он не подлежит налогообложению до момента продажи акций. Тогда из двух акций с одинаковым рыночным риском та, по которой выплачивается более высокий дивиденд, должна иметь более высокую требуемую доходность. В этом случае требуемая доходность будет функцией как рыночного риска, так и дивидендной доходности, т. е. двух факторов.
Более того, не исключено, что зависимость между риском и доходностью является многофакторной. Стивен Росс предложил метод, названный теорией арбитражного ценообразования (Arbitrage Pricing Theory, APT).15 Концепция APT предусматривает возможность включения любого количества факторов риска, так что требуемая доходность может быть функцией трех, четырех или даже большего числа факторов. Следует заметить, что APT базируется на сложной математической и статистической теории, рассмотрение которой выходит за рамки данного текста. Хотя модель APT широко обсуждается в современной научной литературе, практическое ее использование до настоящего времени было ограничено. Тем не менее ситуация меняется, поэтому будущие специалисты в области финансового менеджмента должны по крайней мере иметь общее представление об этой теории.
Теория САРМ утверждает, что требуемая доходность каждой акции равна безрисковой доходности, сложенной с произведением рыночной премии за риск и ß -коэффициента акции:
 (3.5)
(3.5)
Фактическая доходность,  , рассчитывается по формуле
, рассчитывается по формуле
 (3.6)
(3.6)
Доходность рынка,  , зависит от множества факторов, таких как экономическая ситуация в стране, оцениваемая валовым внутренним продуктом, стабильность мировой экономики, темп инфляции, изменения в налоговом законодательстве и т. д. Акции различных компаний неодинаково подвержены влиянию этих факторов. Таким образом, очевидно, что требуемая и фактическая доходность любой акции — это функция не одного фактора (среднерыночная доходность), а нескольких экономических факторов. Тогда можно преобразовать формулу (3.6):
, зависит от множества факторов, таких как экономическая ситуация в стране, оцениваемая валовым внутренним продуктом, стабильность мировой экономики, темп инфляции, изменения в налоговом законодательстве и т. д. Акции различных компаний неодинаково подвержены влиянию этих факторов. Таким образом, очевидно, что требуемая и фактическая доходность любой акции — это функция не одного фактора (среднерыночная доходность), а нескольких экономических факторов. Тогда можно преобразовать формулу (3.6):
 (3.7)
(3.7)
где  — фактическая доходность акции i;
— фактическая доходность акции i;  — ожидаемая доходность акции i;
— ожидаемая доходность акции i;  — фактическое значение экономического фактора j;
— фактическое значение экономического фактора j;  — ожидаемое значение фактора j;
— ожидаемое значение фактора j;  — чувствительность акции i к экономическому фактору j,
— чувствительность акции i к экономическому фактору j,  — влияние специфических факторов на изменение фактической доходности акции г. Формула ß.7) показывает, что фактическая доходность любой акции равна ожидаемой доходности акции, сложенной с величиной прироста или уменьшения, которая зависит: 1) от изменения основных экономических факторов, 2) от чувствительности акции к этим изменениям и 3) от фактора случайности, отражающего специфические для фирмы или отрасли условия деятельности.
— влияние специфических факторов на изменение фактической доходности акции г. Формула ß.7) показывает, что фактическая доходность любой акции равна ожидаемой доходности акции, сложенной с величиной прироста или уменьшения, которая зависит: 1) от изменения основных экономических факторов, 2) от чувствительности акции к этим изменениям и 3) от фактора случайности, отражающего специфические для фирмы или отрасли условия деятельности.
Различные акции не одинаково чувствительны к тем или иным факторам, а доходность каждого портфеля зависит от изменения основных факторов. Теоретически можно сформировать такой портфель ценных бумаг, чтобы он был безрисковым и чистые инвестиции в нем были нулевыми (т. е. некоторые акции продаются при игре на понижение, а выручка от их продажи используется для покупки акций при игре на повышение). Такой портфель нулевых инвестиций должен иметь нулевую ожидаемую доходность, поскольку в противном случае возникнут арбитражные операции, в результате которых цены на акции будут меняться до тех пор, пока ожидаемая доходность портфеля не станет равна нулю. Модель аналога линии SML в арбитражной теории выводится из ß.7) с помощью сложных математических выкладок и некоторых допущений, например допущения о возможности «коротких продаж»:16
 (3.8)
(3.8)
где  — требуемая доходность портфеля с единичной чувствительностью к j- му экономическому фактору (ßj = 1.0) и нулевой чувствительностью (ßj = 0) к другим факторам. Заметим, что ß.8) идентична по форме уравнению SML, но она позволяет отразить требуемую доходность акции как функцию многих факторов.
— требуемая доходность портфеля с единичной чувствительностью к j- му экономическому фактору (ßj = 1.0) и нулевой чувствительностью (ßj = 0) к другим факторам. Заметим, что ß.8) идентична по форме уравнению SML, но она позволяет отразить требуемую доходность акции как функцию многих факторов.
Для иллюстрации концепции APT предположим, что доходность всех акций зависит только от трех факторов риска: инфляции, объемов промышленного производства и степени неприятия риска (цена риска принимается в размере разницы в доходах по дешевым низкодоходным облигациям и государственным облигациям). Далее предположим: 1) безрисковая доходность равна 8.0%; 2) требуемая доходность равна 13% для портфеля с единичной чувствительностью к темпу инфляции (ß = 1.0) и нулевой чувствительностью к изменению объема промышленного производства и изменению степени неприятия риска (ß = 0.0); 3) требуемая доходность для портфеля с единичной чувствительностью к изменению объема промышленного производства и нулевой чувствительностью к темпу инфляции и изменению степени неприятия риска равна 10.0%; 4) требуемая доходность равна 6% для рискового портфеля, обладающего единичной чувствительностью к изменению неприятия риска и нулевой чувствительностью к изменению темпа инфляции и объемов промышленного производства. Наконец, предположим, что акция i имеет значения чувствительности к факторам (ß -коэффициенты), равные 0.9 для портфеля, реагирующего на изменения темпа инфляции, 1.2 для портфеля, реагирующего на изменения объема промышленного производства, и —0.7 для портфеля, реагирующего на изменения степени неприятия риска. Тогда требуемая доходность для акции г, согласно APT, должна быть равна 16.3%:

|
Заметим, что если требуемая доходность на рынке составляет 15.0% и акция i имеет ß, вычисляемую по модели САРМ, равную 1.1, то требуемая доходность, определяемая по САРМ, была бы

|
Главное теоретическое преимущество APT состоит в том, что она включает в рассмотрение влияние нескольких экономических факторов на изменение доходности отдельных акций, тогда как САРМ предполагает, что воздействие всех факторов, кроме специфических для фирмы, может быть выражено единственным критерием — изменчивостью акции относительно рыночного портфеля. К тому же APT предусматривает меньшее количество исходных допущений, чем САРМ, и, следовательно, представляет собой более обобщенную теорию. Наиболее важным является отсутствие в APT требования САРМ о том, чтобы все инвесторы владели рыночным портфелем, что, естественно, не встречается на практике. Концепция APT имеет тем не менее ряд узких мест, самым серьезным из которых является то, что в рамках APT не обосновывается заранее перечень факторов. Основываясь на эмпирических данных, некоторые исследователи полагают, что только три или четыре фактора следует принимать во внимание; чаще всего называют инфляцию, изменение объема промышленного производства, разность в доходности между низко- и высококачественными облигациями и изменение структуры процентных ставок.
Сторонники APT отмечают, что в действительности выделение релевантных факторов не является столь уж необходимым. Для определения параметров APT можно воспользоваться математическим аппаратом факторного анализа. Изначально в расчет принимаются данные о сотнях и даже тысячах акций, затем формируются несколько различных портфелей, не коррелирующих тесно между собой по показателю доходности. Таким образом, в этой совокупности портфелей каждый из них испытывает более сильное воздействие какого-то одного из неизвестных факторов. Затем требуемая доходность каждого портфеля рассматривается как  для этого фактора, а чувствительность доходности каждой отдельной акции к доходности этого портфеля становится чувствительностью фактора (ß). К сожалению, результаты факторного анализа нелегко интерпретировать, так как он не позволяет глубоко проникнуть в сущность основных экономических составляющих риска.
для этого фактора, а чувствительность доходности каждой отдельной акции к доходности этого портфеля становится чувствительностью фактора (ß). К сожалению, результаты факторного анализа нелегко интерпретировать, так как он не позволяет глубоко проникнуть в сущность основных экономических составляющих риска.
Концепция APT находится на ранней стадии развития и пока не может ответить на многие возникающие вопросы. Тем не менее, основная предпосылка APT, заключающаяся в том, что доходность является функцией не одного, а нескольких факторов, крайне привлекательна. Если эти факторы смогут быть выявлены и если APT найдет признание у практиков, то она в состоянии заменить САРМ в качестве основной модели, описывающей зависимость между риском и доходностью.
Вопросы для самопроверки
Каково главное различие между APT и САРМ?
Опишите основные недостатки APT.
Резюме
В главе 3 завершается рассмотрение вопросов, посвященных взаимосвязи риска и доходности. Целью главы было: 1) показать, как включение в портфель безрисковых активов влияет на принимаемые инвестором решения инвестиционного характера, и 2) объяснить, как степень риска воздействует на доходность.
Ниже приведен перечень понятий, рассмотренных в данной главе.
• Модель оценки доходности финансовых активов (САРМ) описывает зависимость между рыночным риском и требуемой доходностью.
• САРМ базируется на системе исходных допущений.
• Линия рынка капитала (CML) отражает зависимость риск—доходность для эффективных портфелей, т. е. для портфелей, сочетающих рисковые и безрисковые активы.
• Линия рынка ценных бумаг отражает зависимость риск—доходность для отдельных акций. Требуемая доходность любой акции равна безрисковой норме, сложенной с произведением премии за рыночный риск и ß -коэффициента акции:

• ß -коэффициент акции i (ß i) — это мера рыночного риска акции. Он измеряет изменчивость доходности акции по отношению к доходности средне рыночного портфеля.
• ß -коэффициент связан с наклоном характеристической линии акции, представляющей собой графическое изображение уравнения регрессии, построенного по статистическим данным о доходности i-й акции и среднерыночной доходности.
• По сравнению со средней акцией, ß которой, по определению, равна единице, доходности акции с большим значением ß свойственна большая колеблемость; верно и обратное — меньше значение ß, меньше колеблемость.
• ß портфеля — это средневзвешенное значение ß -коэффициентов ценных бумаг, включенных в портфель.
• Существует ряд причин, по которым требуемая и ожидаемая доходности не совпадают. В их числе: 1) изменение безрисковой ставки ввиду пересмотра ожидаемого темпа инфляции, 2) изменение ß; 3) переоценка отношения инвестора к риску.
• САРМ хорошо обоснована с позиции теории, однако она не может быть подтверждена эмпирически, ее параметры с трудом поддаются оценке. Поэтому применение САРМ на практике ограничено.
С целью преодоления отмеченных недостатков САРМ были предприняты попытки разработки альтернативных моделей риск—доходность; теория арбитражного ценообразования (APT) — наиболее перспективная из новых моделей.
В следующей главе будет показано, как требуемая доходность финансового актива влияет на его цену. Большая часть остальных глав будет посвяшена рассмотрению методов, с помощью которых управленческий персонал фирмы может влиять на рисковость своих акций и, следовательно, их цену.
Вопросы
3.1. Дайте определение следующих понятий (используйте при ответе соответствующие формулы и графики):
а) модель оценки доходности финансовых активов (САРМ);
б) линия рынка капитала (CML);
в) рыночный риск, диверсифицируемый риск, релевантный риск;
г) ß -коэффициент, ß -коэффициент средней акции, ß А = ß М;
д) линия рынка ценных бумаг (SML), уравнение SML;
е) рыночная премия за риск;
ж) средняя акция;
з) характеристическая линия;
и) теория арбитражного ценообразования (APT).
3.2. Ценная бумага А имеет ожидаемую доходность 6%, среднее квадратическое отклонение от ожидаемой доходности 30%, коэффициент корреляции с рынком -0.25 и ß -коэффициент -0.5. Ценная бумага В имеет ожидаемую доходность 11%, среднее квадратическое отклонение 10%, корреляцию с рынком 0.75 и ß -коэффициент 0.5. Какая из ценных бумаг является более рисковой? Почему?
3.3. В случае увеличения степени неприятия риска со стороны инвестора на какие акции премия за риск возрастет больше и на какие меньше: на акции с высоким значением ß или с низким? Объясните.
Задачи
3.1. Анализ рыночного риска. Фирма «Bowers» имеет следующие данные относительно доходности потенциального проекта и рынка:
| Состояние экономики | Вероятность | Доходность, % | |
| рынок | проект | ||
| Глубокий спад | 0.05 | - 20 | - 30 |
| Умеренный спад | 0.25 | ||
| Среднее состояние | 0.35 | ||
| Умеренное оживление | 0.20 | ||
| Быстрый подъем | 0.15 |
Финансовые аналитики компании дали предварительную оценку безрисковой доходности 8%.
а. Какова ожидаемая доходность проекта и на рынке в среднем?
б. Чему равно значение ß для проекта и рынка?
в. Какова требуемая доходность проекта согласно модели САРМ?
г. Следует ли принять проект?
3.2. Рыночный и общий риск. Ваш эксцентричный дядюшка умер и оставил вам 100000 дол. Однако по условиям завещания вся сумма должна быть вложена в обыкновенные акции, а именно 50 000 дол. в акции одной фирмы (портфель из одной акции), а другие 50000 дол. в портфель из 100 акций. Вы очень не любите рисковать и хотите свести возможный риск к минимуму для каждого вклада по 50000 дол.
а. Как вы выберете портфель из одной акции?
б. Как вы выберете акции для портфеля из 100 акций?
в. Должны ли вы рассматривать степень риска вашего портфеля из одной акции изолированно или должны учитывать, что в действительности у вас 101 акция?
3.3. Линия рынка ценных бумаг. Предположим,  = 10%,
= 10%, 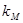 = 14%, а
= 14%, а 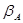 = 1.4.
= 1.4.
а. Рассчитайте требуемую доходность акции A (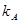 ).
).
б. Предположим, что  увеличивается до 11% или падает до 9%. Наклон линии рынка ценных бумаг остается постоянным. Как это повлияет на
увеличивается до 11% или падает до 9%. Наклон линии рынка ценных бумаг остается постоянным. Как это повлияет на 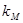 и
и 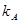 ?
?
в. Теперь допустим, что  остается равным 10%,
остается равным 10%, 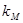 возрастает до 15% или падает до 12%- Наклон линии рынка ценных бумаг не остается постоянным. Как это повлияет на
возрастает до 15% или падает до 12%- Наклон линии рынка ценных бумаг не остается постоянным. Как это повлияет на 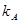 .
.
г. Теперь предположим, что  остается равным 10%,
остается равным 10%, 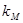 = 14%, но ß возрастает до 1.6 или падает до 0.75. Как это повлияет на
= 14%, но ß возрастает до 1.6 или падает до 0.75. Как это повлияет на 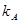 ?
?
3.4. Линия рынка ценных бумаг. «Dalton Bigbee» представляет собой крупную сеть универмагов. Акции этой фирмы имеют /3 = 0.8, безрисковая доходность составляет 8%, а требуемая доходность на рынке — 13%.
а. Какова премия за рыночный риск?
б. Какова требуемая доходность акций «Bigbee»?
в. Постройте SML и укажите на графике требуемую доходность акций компании.
г. Какова будет требуемая доходность акций «Bigbee», если инфляционные ожидания возрастут на 2 процентных пункта? (Допустим, что фактор неприятия риска не изменится).
д. Вернемся к безрисковой ставке 8%. Какова будет требуемая доходность акций «Bigbee» при условии возрастания степени неприятия риска инвестором, а также роста премии за рыночный риск до 7%?
е. Вернемся к премии за рыночный риск, равной 5%. Какова будет требуемая доходность акций фирмы, если ß акций возрастет до 1.2?
3.5. ß -коэффициент портфеля и линия рынка ценных бумаг. Инвестиционный фонд «Vantage» инвестировал 400 млн. дол. в акции пяти фирм:
| Фирма.....................……………………. | A | B | C | D | E |
| Инвестиция, млн. дол.......……………. | |||||
| ß -коэффициент.............………………. | 0.5 | 2.0 | 4.0 | 1.0 | 3.0 |
ß -коэффициент портфеля фонда может быть рассчитан по формуле средней арифметической взвешенной значений ß -коэффициентов отдельных активов. Текущая безрисковая доходность равна 7%, а рыночная доходность имеет следующее распределение на планируемый год:
| Вероятность................………………… | 0.1 | 0.2 | 0.4 | 0.2 | 0.1 |
| Рыночная доходность, %....…………… |
а. Рассчитайте уравнение SML.
б. Вычислите требуемую доходность инвестиционного портфеля фонда.
в. Предположим, руководство получает предложение купить новые акции. Для заключения сделки требуется инвестировать в акции 50 млн. дол.; это даст ожидаемый доход в 16%; ß новых акций равна 2.5. Следует ли покупать новые акции? При какой ожидаемой доходности руководство не будет заинтересовано в покупке акций?
3.6. Характеристическая линия и линия рынка ценных бумаг. Вам предлагается следующий набор данных:
| Год...................... | |||||||
| Фактическая доходность за прошлые периоды,%: | |||||||
| Акции NYSE............ | - 26.5 | 37.2 | 23.8 | - 7.2 | 6.6 | 20.5 | 30.6 |
| Акция X............... | - 14.0 | 23.0 | 17.5 | 2.0 | 8.1 | 19.4 | 18.2 |
а. Рассчитайте значение ß -коэффициента акции X или с помощью калькулятора (компьютера), или путем построения линии регрессии на графике.
б. По формуле средней арифметической рассчитайте значения доходности акции X в среднем на рынке за данный период. Вычислите средние квадратические отклонения доходности для акций X и NYSE.
в. Предположим, что: 1) в будущем сохранится ситуация, соответствующая годам с 1 по 7 (т. е.  останутся без изменения), и 2) акция X находится в равновесии, ее характеристики лежат на линии рынка ценных бумаг. Какова при этом безрисковая доходность?
останутся без изменения), и 2) акция X находится в равновесии, ее характеристики лежат на линии рынка ценных бумаг. Какова при этом безрисковая доходность?
г. Начертите линию рынка ценных бумаг.
д. Допустим, вы владеете большим, хорошо диверсифицированным портфелем и собираетесь добавить к нему либо еще акций X, либо других акций Y, которые имеют то же значение ß -коэффициента, что и акции X, но более высокое среднее квадратическое отклонение доходности. Акции X и Y имеют одинаковую ожидаемую доходность, т. е.  10.6%. Какие акции вы выберете?
10.6%. Какие акции вы выберете?
3.7. Характеристическая линия. Вам предлагается следующий ряд данных:
| Год | Фактическая доходность за прошлые периоды, % | |
| NYSE | Акция Y | |
| 4.0 | 3.0 | |
| 14.3 | 18.2 | |
| 19.0 | 9.1 | |
| - 14.7 | - 6.0 | |
| - 26.5 | - 15.3 | |
| 37.2 | 33.1 | |
| 23.8 | 6.1 | |
| - 7.2 | 3.2 | |
| 6.6 | 14.8 | |
| 20.5 | 24.1 | |
| 30.6 | 18.0 | |
| Среднее значение | 9.8 | 9.8 |
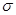
| 19.6 | 13.8 |
а. Начертите график рассеяния, характеризующий зависимость между доходностью акции У и рыночной доходностью, а затем постройте приблизительную линию регрессии. Каково приближенное значение ß -коэффициента? Уточните значение ß с помощью калькулятора (компьютера).
б. Поясните, как линия регрессии и ß -коэффициент характеризуют степень изменчивости и относительного риска акции Y по сравнению с другими.
в. Допустим, что исходные данные были рассеяны в большей степени, но положение линии регрессии не изменилось. Как это могло бы повлиять: 1) на риск фирмы, если в ее портфеле акции только одной компании, и 2) на фактическую премию за риск владения таким портфелем в условиях действия САРМ?
г. Допустим, что линия регрессии указывает на обратную связь, т. е. ß -коэффициент отрицателен. Как это сказывается: 1) на относительной рисковости акции Y, 2) на ее корреляции с рынком и 3) на ее вероятной премии за риск?
д. Постройте для примера график распределения вероятностей доходности: 1) портфеля, состоящего только из акции Y; 2) портфеля из 100 разных акций, каждая из которых имеет ß -коэффициент, равный ß -коэффициенту акции Y; 3) портфеля из всех акций (т. е. распределение доходности на рынке). Используйте в качестве ожидаемой доходности для акции Y и для рынка в целом среднюю арифметическую при условии, что распределение нормально. Являются ли ожидаемые доходности приемлемыми, если 
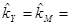 9.8%?
9.8%?
3.8. Сравнение линии рынка ценных бумаг с линией рынка капитала. ß -коэффициент какого-либо актива может быть выражен как функция коэффициента корреляции этого актива с рынком следующим образом:

а. Подставьте это выражение в (3.2). Вы получили альтернативную формулу SML.
б. Сравните полученную формулу с (3.1). Какое вы наблюдаете сходство? Какой отсюда можно сделать вывод?
Поиск по сайту: