Вопрос для самопроверки

Объясните следующее утверждение: «Риск отдельного проекта, рассматриваемого изолированно, может выглядеть достаточно высоким, однако при оценке его с точки зрения влияния проекта на риск акционеров он может оказаться вполне приемлемым».

Концепция β -коэффициента

Характеристики средней акции, по определению, должны варьировать в со­ответствии с изменением ситуации на рынке, измеряемой некоторым индексом, например индексом S&P 500 или индексом Нью-Йоркской фондовой биржи. Та­кая акция имеет β -коэффициент, равный 1.0; это означает, что, например, при изменении ситуации на рынке вверх или вниз на 10 процентных пунктов ха­рактеристики акции меняются в том же направлении на 10 процентных пунк­тов. Доходность портфеля из акций с β = 1.0 будет повышаться и понижаться одновременно с изменением среднего рыночного курса, а риск портфеля будет совпадать со средним на рынке. Если акция имеет β = 0.5, ее характеристики меняются в два раза медленнее, чем в среднем на рынке; портфель, состоящий из таких ак­ций, будет иметь риск, равный половине риска портфеля из акций с β = 1.0. С другой сто­роны, если β = 2.0, то изменчивость характе­ристик акции в два раза выше по сравнению со средней акцией, поэтому портфель, состоящий из подобных акций, в два раза рисковее сред­него портфеля.

β -коэффициенты подсчитываются и публи­куются такими агентствами, как «Merrill Lynch», «Value Line», и многими другими. Не­которые данные агентства «Value Line» приве­дены в табл. З.1.9 β -коэффициент акций большинства компаний варьирует от 0.75 до 1.5, а среднее значение для всех акц по определению, равно 1.0.

β -коэффициент портфеля

β -коэффициент любого портфеля ценных бумаг, β_p, рассчитывается по фор­муле средней арифметической взвешенной:

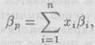(3.3)

где x_i — доля i-й ценной бумаги в портфеле. Очевидно, что добавление в порт­фель акции, имеющей β больше единицы, увеличивает значение β_p, т. е. повы­шает рисковость портфеля. При добавлении акции с β < 1 рисковость портфеля снижается. Таким образом, так как β акции измеряет ее вклад в рисковость портфеля, β является подходящим измерителем степени риска акции.

Проиллюстрируем это утверждение. Допустим, вы владеете портфелем ак­ций, стоимость которого составляет 100000 дол., по 10000 дол. вложено в 10 видов акций, и каждая из них имеет β = 0.8, в этом случае портфель имеет β_p = 0.8. Он будет менее рисковым, чем среднерыночный портфель; на практике это выражается в относительно небольших колебаниях цен акций в портфеле и, следовательно, в относительно небольших изменениях доходности.

Теперь предположим, что вы продали одну из акций портфеля и заменили ее акцией с β = 2.0. Такой акт приведет к росту рисковости портфеля с β_{p 1} = 0.8 до β_p 2 = 0.92, что следует из (3.3):

Если бы в портфель была добавлена акция с β = 0.6, то β портфеля изменилась бы с 0.8 до 0.78.

Расчет β -коэффициентов: характеристическая линия

Когда проф. Шарп разрабатывал теорию САРМ, он обратил внимание на то, что рыночный риск любой акции может быть оценен на основе анализа тенден­ции изменения ее характеристик по отношению к среднерыночным их значе­ниям. Разработанный им способ определения рыночного риска иллюстрируется с помощью рис. 3.6 и будет объяснен в последующих разделах.10

Значения фактической доходности акции, , и доходности на рынке в сред­нем, , за истекшие периоды приведены в нижней части рис. 3.6. Заметим, что когда доходность на рынке в среднем высока, то и доходность акции J имеет тенденцию к росту; напротив, спад на рынке вызывает снижение доход­ности акции. Эта связь выражается более точно регрессионной зависимостью, показанной на рис. 3.6.

Здесь используется простейшая линейная зависимость, представленная уравнением регрессии Y = а + β Х + е. Таким образом, доходность акции J в конкретный момент зависит от ситуации на рынке ценных бумаг, характе­ризуемой показателем , и случайных явлений, влияющих прежде всего на характеристики акции J.

Параметры уравнения регрессии рассчитываются методом наименьших ква­дратов с использованием специализированного калькулятора или компьютера, имеющего программу обработки статистических данных, как например Lotus 1-2-3. График уравнения регрессии называется линией регрессии. Шарп назвал линию регрессии характеристической линией акции. Таким образом, β ак­ции — это величина наклона ее характеристической линии.

Для иллюстрации рассмотрим процесс построения уравнения регрессии по упрощенному алгоритму, без использования специального аппарата. На основе имеющихся данных можно приблизительно провести прямую, а далее уточнить параметры уравнения Y = а + β Х. Так, коэффициент а — это точка, в которой линия пересекает вертикальную ось. Коэффициент β может быть определен с помощью соотношения приростов показателей X и Y. Например, по данным рис. 3.6 видно, что возрастает от —8.9 до +7.1% при изменении с 0.0 до 10.0%. Таким образом, коэффициент β может быть рассчитан по формуле

Более точные расчеты могут быть выполнены с помощью известных стати­стических формул, в частности

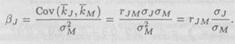
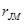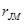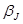Таким образом, β акции, а следовательно, и характеризуемый ею рыночный риск акции зависят: 1) от ее корреляции с рынком акций в целом, ; 2) от ее собственной изменчивости, ; 3) от изменчивости рынка, . В примере на рис. 3.6 = 0.91, = 26.5% и = 15.1%. Следовательно, = 0.91-26.5%: 15.1% = 1.60.

Год	Акция J( ), %	Рынок ,%
	38.6	23.8
	-24.7	-7.2
	12.3	6.6
	8.2	20.5
	40.1	30.6
	14.9	14.9
	26.5	15.1

Рис. 3.6. Расчет ß -коэффициентов.

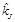— фактическая доходность акции J ( и 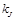— ожидаемая и требуемая доходность соответственно); — фактическая доходность на рынке в среднем; 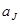— точка пе­ресечения характеристической линии акции J с осью ординат; 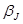— наклон, или ß- коэффициент, акции J; 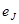— случайная ошибка, отражающая различие между факти­ческой доходностью акции J в данном году и доходностью, прогнозируемой с помощью линии регрессии.

Несколько замечаний о ß -коэффициентах

Теперь, после того как мы изобразили графически фактические нормы при­были акции J иопределили ее ß -коэффициент, необходимо отметить следующие моменты.

1. Предполагается, что прогнозируемые значения доходности акции, 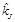, и доходности акций на рынке в среднем, , связаны линейной зависимостью:

(3.4)

Другими словами, подразумевается, что сложившаяся в прошлом связь между акцией J и рынком в целом и представленная характеристической линией со­хранится и в будущем.11

2. Каждая фирма помимо реагирования на изменение рынка в целом стал­кивается также с явлениями, существенными лишь для нее и не зависящими от общего состояния экономики. Такие явления приводят к изменению доходности акций фирмы J вне зависимости от ситуации на рынке в целом; эти случайные явления объясняются случайной ошибкой ej. До того как событие произойдет, ожидаемая величина случайной ошибки равна нулю; в результате этого собы­тия она может быть как положительной, так и отрицательной. Этот компонент общего риска называется диверсифицируемым, или специфическим для компа­нии, риском (diversifiable, or company-specific, risk); рациональный инвестор устраняет его влияние, составляя диверсифицированный портфель акций.

3. Коэффициент регрессии ß (ß -коэффициент) — это индекс чувствитель­ности к ситуации на рынке; он измеряет относительную изменчивость данной акции по сравнению со средней акцией, или «рынком». Тенденция отдельной акции изменяться вместе с рынком содержит риск, так как цены на рынке ко­леблются и колебания не могут быть элиминированы. Этот компонент общего риска называется рыночным, или недиверсифицируемым, риском (market, or nondiversifiable, risk). Даже хорошо диверсифицированные портфели подвер­жены рыночному риску.

4. Зависимость между общим риском акции, рыночным риском и диверси­фицируемым риском может быть выражена следующим образом:

где — дисперсия (или общий риск) акции J; 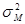— дисперсия рынка; 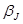— ß -коэффициент акции J; 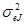— дисперсия регрессионной ошибки акции J (ди­версифицируемый риск).

5. Если на рисунке, подобном рис. 3.6, все точки лежат точно на линии регрессии, величина дисперсии, 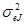будет равна нулю, а общий риск акции со­впадает с рыночным. С другой стороны, если точки широко разбросаны вокруг линии регрессии, значительная часть общего риска акции может быть диверси­фицирована. Акции крупного, хорошо диверсифицированного фонда отобража­ются точками, лежащими очень близко к линии регрессии.

6. Если бы рынок акций не был подвержен колебаниям, акции не имели бы рыночного риска. В реальной жизни рынок подвержен изменениям, по­этому этот риск всегда присутствует; даже обладая хорошо диверсифицирован­ным портфелем, инвестор тем не менее может понести убытки в случае падения рыночного курса. В последние годы среднее квадратическое отклонение рыноч­ной доходности, , колеблется в основном около 15%. Однако за один день, 19 октября 1987 г., индекс Доу—Джонса для акций промышленных предприя­тий, один из основных фондовых индексов, упал на 23%.

7. ß — это показатель относительного рыночного риска; фактический рыночный риск акции J равен . Рыночный риск также может быть выражен в форме среднего квадратического отклонения, 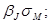таким образом, рыночный риск акции J равен 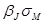= 1.6*15.1% = 24%, а ее общий риск 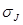= 26.5%. Для любого состояния неустойчивости рынка, измеряемой средним квадратическим отклонением, , чем выше ß акции, тем выше ее рыночный риск. Если ß равна нулю, акция не имеет рыночного риска, а если ß составляет 1.0, то акция имеет в точности такой же риск, как и в среднем на рынке ( ), припредположении, что акция находится в диверсифицированном портфеле.

8. Диверсифицируемый риск может и должен быть устранен путем диверсификации, поэтому релевантным является рыночный, а не общий риск. Если
у акции J ß = 0.5, то релевантный риск будет 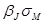= 0.5 • 15.1% = 7.55%. Портфель из таких акций имеет среднее квадратическое отклонение ожидаемой доходности 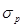= 7.55%, или 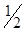среднего квадратического отклонения ожида­емой доходности портфеля, состоящего из средних акций (ß = 1.0). Если бы акция J была акцией свысокой ß (ß = 2.0), то ее релевантный риск был бы 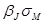= 2.0 * 15.1%= =30.2%. Портфель из акций с ß = 2.0 имеет 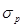= 30.2%;
таким образом, его риск в два раза выше риска портфеля из средних акций.

9. Премия за риск владения акцией рассчитывается исходя из рыночного,
а не общего риска: RP_j = (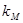 — . Инвестор может иметь только одну
акцию J и, следовательно, иметь дело с общим риском. При этом он стремится
к получению дохода, основанного на данном риске. Если остальные инвесторы
владеют хорошо диверсифицированным портфелем акций, они сталкиваются с
меньшим риском, чем риск акции J. Следовательно, если акция J имеет доход­
ность достаточно высокую, чтобы обеспечить запросы данного инвестора, она
представляет собой выгодное приобретение и для других инвесторов, которые
захотят купить ее, что приведет к росту цены и снижению доходности. По­
скольку большинство финансовых активов принадлежит инвесторам, диверси­
фицирующим свои портфели, а любая ценная бумага может иметь только один
уровень цены и, следовательно, только один уровень доходности, то подобные
операции на рынке автоматически приведут к установлению релевантного, ры­
ночного риска данной акции.

Вопросы для самопроверки

Объясните понятие ß - коэффициента. Проиллюстрируйте свое объяснение графиком, изображающим характеристические линии для акций с низким, средним и высоким рис­ком. (Указание: три линии характеристик должны пересечься в точке 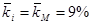, соответствующей величине предполагаемой безрисковой ставки).

Какая связь существует между общим риском, рыночным риском и диверсифициру­емым риском?

Поиск по сайту: