 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Оценка доходности по четырем инвестиционным альтернативам
| Состояние экономики | Вероятность | Казна- чейские векселя, % | Доходность инвестиций при данном состоянии экономики. | ||
| корпорационные облигации | проект 1 | проект 2 | |||
| Глубокий спад Незначительный спад Стагнация | 0.05 0.20 0.50 | 8.0 8.0 8.0 | 12.0 10.0 9.0 | -3.0 6.0 11.0 | -2.0 9.0 12.0 |
| Незначительный подъем | 0.20 | 8.0 | 8.5 | 14.0 | 15.0 |
| Сильный подъем | 0.05 | 8.0 | 8.0 | 19.0 | 26.0 |
| Ожидаемая доходность | — | 8.0 | 9.2 | 10.3 | 12.0 |
Примечание. Доходность, соответствующую различным состояниям экономики, следует рассматривать как интервал значений, а отдельные ее значения — как точки внутри этого интервала. Например, 10%-ная доходность облигации корпорации при незначительном спаде представляют собой наиболее вероятное значение доходности при данном состоянии экономики, а точечное значение используется для удобства расчетов.
соответствующих периодов владения активами. Поскольку значения доходности не известны с полной определенностью, эти три вида инвестиций являются рисковыми.
Распределения вероятностей бывают дискретными или непрерывными.2 Дискретное распределение вероятностей имеет конечное число исходов; так, в табл. 2.1 приведены дискретные распределения вероятностей. Доходность казначейских векселей принимает только одно возможное значение, тогда как каждая из трех оставшихся альтернатив имеет пять возможных исходов. Каждому исходу поставлена в соответствие вероятность его появления. Например, вероятность того, что казначейские векселя будут иметь доходность 8%, равна 1.00, а вероятность того, что доходность казначейских корпоративных облигаций составит 9%, равна 0.50.
Если умножить каждый исход на вероятность его появления, а затем сложить полученные результаты, мы получим средневзвешенную исходов. Весами служат соответствующие вероятности, а средневзвешенная представляет собой ожидаемое
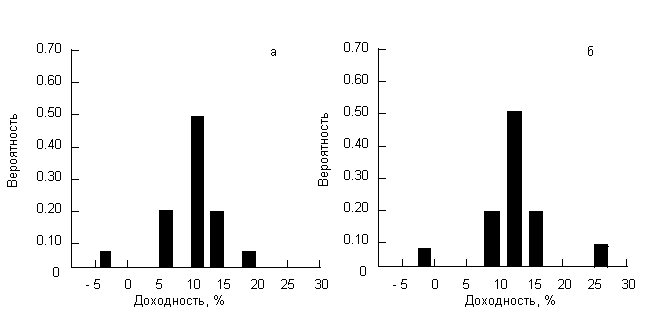
Рис. 2.1. Графическое представление дискретного распределения вероятностей.
а — проект 1; б — проект 2.
значение. Так как исходами являются доходности, ожидаемое значение — это ожидаемая доходность (expected rate of return, 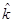 ), которую можно представить в следующем виде:
), которую можно представить в следующем виде:
 (2.1)
(2.1)
где  — i-й возможный исход; Рi — вероятность появления i-гo исхода; n — число возможных исходов.
— i-й возможный исход; Рi — вероятность появления i-гo исхода; n — число возможных исходов.
Используя (2.1), находим, что ожидаемая доходность проекта 2 равна 12.0%:

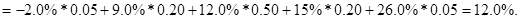
Ожидаемые доходности трех других альтернативных вариантов инвестирования найдены аналогичным образом (табл. 2.1).
Дискретные распределения вероятностей могут быть представлены графически или в табличной форме. На рис. 2.1 приведены столбиковые диаграммы (или гистограммы) проектов 1 и 2. Возможные значения доходности проекта 1 принадлежат промежутку от -3.0 до +19.0%, а проекта 2 — от -2.0 до +26.0%. Отметим, что высота каждого столбца представляет собой вероятность появления соответствующего исхода, а сумма этих вероятностей по каждому варианту равна 1.00. Отметим также, что распределение значений доходности проекта 2 симметрично, тогда как соответствующее распределение для проекта 1 имеет левостороннюю асимметрию. Аналогичные диаграммы для казначейских векселей и корпорационных облигаций показали бы, что доходность казначейских векселей представлена единственным столбцом, а доходность корпорационных облигаций представлена диаграммой, имеющей правостороннюю асимметрию.
Вопросы для самопроверки
Что такое распределение вероятностей?
Поясните сущность термина «ожидаемая доходность».
Поиск по сайту: