Дисперсия и среднее квадратическое отклонение

Дисперсией называется мера разброса возможных исходов относительно ожидаемого значения: чем выше дисперсия, тем больше разброс. Для расчета дисперсии дискретного распределения используется следующая формула:

(2.2)

Как показывает (2.2), дисперсия есть сумма квадратов отклонений от сред­него ожидаемого значения, взвешенная на вероятность появления каждого от­клонения. Рассчитаем, например, дисперсию доходности проекта 2 по данным табл. 2.1. Нам известно, что ожидаемая доходность проекта, k, равна 12.0%. Следовательно, расчет дисперсии по формуле (2.2) и данным табл. 2.1 произво­дится следующим образом:

Дисперсию измеряют в тех же единицах, что и исходы, в данном случае в про­центах в квадрате.

Поскольку интерпретация термина «процент в квадрате» затруднительна, в качестве другого измерителя разброса индивидуальных значений вокруг сред­него часто используется среднее квадратическое отклонение, представляющее собой квадратный корень из дисперсии:

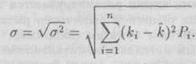
(2.3)

Так, среднее квадратическое отклонение доходности проекта 2 можно найти следующим образом:

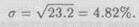
Используя этот показатель в качестве меры разброса, можно сделать ряд полез­ных выводов о распределении исходов. В частности, если распределение явля­ется непрерывным и близким к нормальному, можно утверждать, что 68.3% всех исходов

Таблица 2.2

Оценка доходности и риска четырех альтернативных вариантов инвестирования

Показатель	Варианты инвестирования
казна­чейские векселя	Корпорационные облигации	проект 1	проект 2
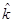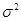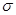1. Ожидаемая доходность (), % 2. Дисперсия () 3. Среднее квадратическое отклонение (), % 4. Коэффициент вариации (CV)	8.00 0.00 0.00   0.00	9.20 0.71 0.84   0.09	10.30 19.31 4.39   0.43	12.00 23.20 4.82   0.40

лежит в пределах одного среднего квадратического отклонения от ожидаемого значения, 99.5% — в пределах двух средних квадратических отклонений и практически все исходы (99.7%) — в пределах трех средних квадратических отклонений.3

В табл. 2.2 приводятся ожидаемые значения доходности, дисперсия и сред­нее квадратическое отклонение по всем четырем альтернативным вариантам ин­вестирования, а также коэффициент вариации, который мы рассмотрим в сле­дующем разделе. Мы видим, что казначейские векселя обладают наименьшими значениями показателей дисперсии и среднего квадратического отклонения, а проекту 2 соответствуют наибольшие их значения.

По данным табл. 2.2 можно, казалось бы, прийти к заключению, что казна­чейские векселя — наименее рисковый вариант инвестирования, а проект 2 — наиболее рисковый. Однако это не всегда верно; перед тем как сделать оконча­тельный вывод, необходимо принять во внимание ряд других факторов, таких как численные значения ожидаемой доходности, асимметрия распределения, до­стоверность наших оценок распределения вероятностей и взаимосвязь каждого актива с другими активами, включенными в портфель инвестиций.4

Поиск по сайту: