 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Риск портфеля
Как было отмечено, ожидаемая доходность портфеля представляет собой средневзвешенную из ожидаемых доходностей отдельных акций, входящих в портфель, а вклад каждой акции в ожидаемую доходность портфеля равен 
. Что касается средних квадратических отклонений портфеля, 
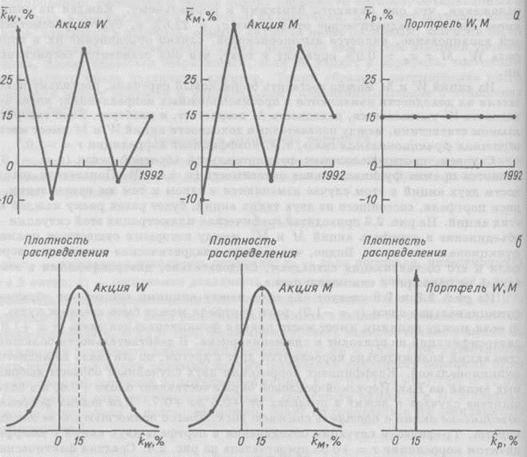
, и составляющих его ценных бумаг, то они подобным алгоритмом уже не связаны. Теоретически можно подобрать две акции, каждая из которых имеет высокий уровень риска, характеризуемый показателем среднего квадратического отклонения, и составить из этих высокорисковых активов портфель, который окажется абсолютно безрисковым, т. е. = 0%. Чтобы проиллюстрировать сказанное, рассмотрим пример, приведенный на рис. 2.2, где показаны фактические значения доходности акций W и М, а также портфеля, в который эти две акции входят равными долями (акции получили названия W и М, поскольку графики их доходности сходны с написанием этих букв). На рис. 2.2, а представлено изменение фактической доходности с течением времени, на рис. 2.2, б — распределения вероятностей значений доходности в предположении, что они являются близкими к нормальному. Каждая из акций имеет среднее квадратическое отклонение 
= 22.6% и, будучи рассмотренной изолированно, является высокорисковой, однако объединение их в портфель W. М с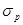 
= 0.0% приводит к тому, что они становятся безрисковыми.
Из акций W и М можно составить безрисковый портфель, поскольку показатели их доходности изменяются в противоположных направлениях: когда доходность W уменьшается, доходность М возрастает, и наоборот. Если говорить языком статистики, между показателями доходности акций W и М имеет место обратная функциональная связь, т. е. коэффициент корреляции r = -1.0.6
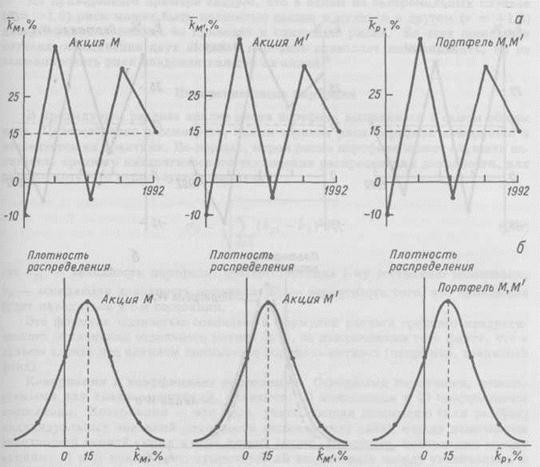
Случаем, противоположным функциональной обратной связи (r = -1.0), является прямая функциональная зависимость (r = +1.0). Показатели доходности двух акций в этом случае изменяются в одном и том же направлении, а риск портфеля, состоящего из двух таких акций, будет равен риску каждой из этих акций. На рис. 2.3 приводится графическая иллюстрация этой ситуации - объединение в портфель акций М и М', между которыми существует прямая функциональная связь. Видно, что средние квадратические отклонения портфеля и его составляющих совпадают, следовательно, диверсификация в этом случае не приводит к снижению риска.
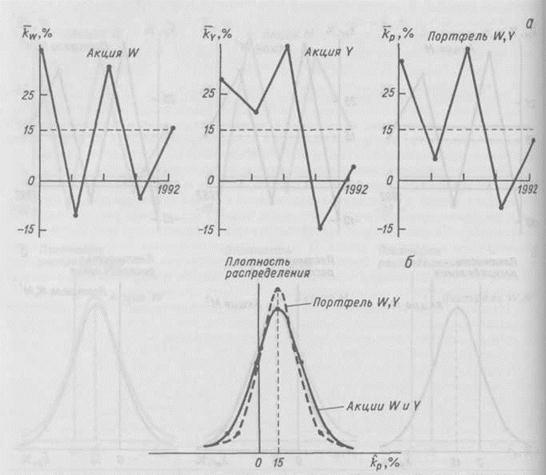
Из рис. 2.2 и 2.3 следует: 1) если между акциями существует обратная функциональная связь (r = —1.0), риск портфеля может быть сведен к нулю, и 2) если между акциями имеет место прямая функциональная связь (r = +0.1), диверсификация не приводит к снижению риска. В действительности большинство акций положительно коррелируют друг с другом, но эта связь не является функциональной. Коэффициент корреляции двух случайным образом выбранных акций на Нью-Йоркской фондовой бирже составляет около +0.6, а в большинстве случаев r лежит в пределах от +0.5 до +0.7. При таких условиях объединение акций в портфель снижает риск, однако полностью его не элиминирует. Графически ситуация объединения в портфель двух акций с коэффициентом корреляции r = +0.65 представлена на рис. 2.4. Средняя фактическая доходность портфеля равна 15.0% и совпадает со средней фактической доходностью каждой из акций. Между тем среднее квадратическое отклонение портфеля, равное 20.6%, меньше, чем среднее квадратическое отклонение любой из акций. Таким образом, риск портфеля не равен среднему из рисков составляющих его акций, а диверсификация приводит к снижению, но не к полному устранению риска.7
| Год | Акция W,
 %
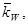| Акция М,
 %
| Портфель W, М,
 %
|
| -10 | |||
| -10 | |||
| -5 | |||
| -5 | |||
| Средняя доходность | |||
| Среднее квадратическое отклонение | 22.6 | 22.6 | 0.0 |
Рис. 2.2. Распределения доходности акций W и М, связанных обратной функциональной связью (r = -1.0), и портфеля W, М.
а — доходность; б — распределение вероятностей значений доходности.
| Год | Акция М,
 ,%
| Акция М',
 ,%
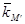| Портфель М, М',
 ,%
|
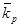| -10 | -10 | -10 | |
| -5 | -5 | - 0 | |
| Средняя доходность | |||
| Среднее квадратическое отклонение | 22.6 | 22.6 | 22.6 |
Рис. 2.3. Распределения доходности акций М и М', связанных прямой функциональной связью (r = +1.0), и портфеля М, М'.
Обозначения те же, что на рис. 2.2.
| Год | Акция W,
 ,%
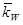| Акция Y,
 ,%
| Портфель W, Y,
,%
|
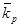| -10 | |||
| -5 | -17 | -11 | |
| Средняя доходность | |||
| Среднее квадратическое отклонение | 22.6 | 22.6 | 20.6 |
Рис. 2.4. Распределения доходности двух коррелирующих акций (r = +0.65) и
портфеля W, Y. Обозначения те же, что на рис. 2.2.
Из приведенного примера следует, что в одном из экстремальных случаев (r = -1.0) риск может быть полностью сведен к нулю, а в другом (r = +1.0) диверсификация вообще не приводит к снижению риска. Во всех остальных случаях объединение двух акций в портфель позволяет лишь снизить, но не элиминировать риск владения каждой из акций.8
Поиск по сайту: