Базовая модель оценки финансовых активов (DCF-модель)

Оценка первичных ценных бумаг, основывающаяся на прогнозировании денежного потока, выполняется по следующей схеме. Во-первых, оценивавается денежный поток, что подразумевает оценку величины денежных поступлений и соответствующего риска в разрезе подпериодов. Во-вторых, требуемая доходность денежного потока устанавливается из расчета риска, с ним связанного, и доходности, которую можно достичь при иных альтернативных вложениях. Требуемая доходность может быть либо постоянной, либо изменяемой в течение анализируемого промежутка времени. В-третьих, денежный поток дисконтируется по требуемой доходности. В-четвертых, дисконтированные величины суммируются для определения стоимости актива. Нижеприведенные схема и формула (4.1) дают формализованное описание данного алгоритма:1

(4.1)

где V₀ — текущая, или приведенная, стоимость актива; CF_t — ожидаемые денежные поступления (приток либо отток) в момент t; k_t — требуемая доходность в период t; n — число периодов, в течение которых ожидается поступление денежных средств. Если денежный поток является регулярным, т. е. поступление или отток денежных средств осуществляется через равные промежутки времени, а требуемая доходность постоянна, формула (4.1) принимает упрощен­ную форму. В этой главе будут рассмотрены как общий случай, представленный (4.1), так и несколько упрощенных форм.

Заметим, что базовая модель оценки может применяться как к материально-вещественным активам, так и к ценным бумагам. Материально-вещественные активы — это имущество в виде земли, зданий, оборудования и даже фирмы в целом. Ценные бумаги — это документы, дающие право на получение части денежного потока, поступающего от эксплуатации материально-вещественных активов. Ценные бумаги делятся на три основных класса: 1) долговые цен­ные бумаги, представляющие собой контрактные обязательства уплатить уста­новленную сумму денег; 2) привилегированные акции, которые также имеют природу договора, однако предоставляемое право на получение части дохода и имущества фирмы может быть исполнено лишь после удовлетворения прав владельцев долговых ценных бумаг и обязательств; 3) обыкновенные акции, ко­торые предоставляют право на получение части дохода и имущества фирмы в остаточном порядке, т. е. после удовлетворения обязательств перед владельцами долговых ценных бумаг и привилегированных акций.

Внутри каждого класса выделяются различные виды ценных бумаг: долго­срочные и краткосрочные долговые обязательства; обязательства, по которым осуществляется периодическая выплата процентов, а сумма основного долга по­гашается единовременно в конце установленного срока; обязательства, по ко­торым погашение суммы основного долга осуществляется постепенно в течение срока ссуды. По одним обязательствам выплачивается фиксированный процент, по другим процент может меняться; иногда платежи осуществляются золотом, серебром или нефтью. Некоторые долговые ценные бумаги и привилегирован­ные акции могут конвертироваться в обыкновенные акции, другие выпускаются под залог имущества, а третьи являются не обеспеченными тем или иным спе­цифическим имуществом.

В зависимости от вида ценной бумаги формула (4.1) может меняться. По­скольку фирмы и инвестиционные институты изобрели множество различных видов ценных бумаг и число их каждый день увеличивается, можно провести всю жизнь, придумывая новые варианты базовой формулы. Поэтому прежде всего рассмотрим модели трех основных видов ценных бумаг: облигации, при­вилегированные акции и обыкновенные акции. Далее в книге будут рассмо­трены вопросы оценки капитальных вложений, а также таких специфических инструментов, как опцион, аренда или слияние фирм.

Вопросы для самопроверки

Почему оценка является важной категорией финансового менеджмента?

Опишите базовую модель оценки финансовых активов.

Оценка облигаций

Наиболее распространенным типом долговых ценных бумаг является обли­гация с денежным потоком в виде постоянных полугодовых процентных плате­жей и номинала, выплачиваемого при погашении. Ценность облигации, как и любого другого актива, определяется приведенной стоимостью ожидаемого де­нежного потока. Следовательно, нужно найти приведенную стоимость аннуитета и единовременно выплачиваемой величины номинала. Поэтому формула (4.1) для такой облигации может быть модифицирована следующим образом:2

(4.2)

где I - годовой купонный доход (I/2 - полугодовой доход); считается, что первая выплата процентов будет произведена через шесть месяцев после приобретения облигации; М — нарицательная стоимость, выплачиваемая при погашении облигации; k_d - требуемая доходность инвестированного капитала; полугодовое наращение делается по ставке kd/2; n - число лет до погашения облигаций; для расчета дисконтированного потока n удваивается, поскольку проценты выплачиваются дважды в год.

В качестве примера рассчитаем приведенную стоимость 12%-ной облигации номиналом 1000 дол. с полугодовой выплатой процентов и сроком погашения 10 лет при k_d 10%:

Расчеты можно делать с помощью либо специализированного калькулятора, либо финансовых таблиц. В последнем случае алгоритм расчета таков:3

Доходность облигации без права досрочного погашения

Модель оценки, представленная формулой (4.2), может использоваться для расчета доходности облигации без права досрочного ее погашения (Yield to Matu­rity, YTM), или безотзывные облигации. Если известны данные о текущей ры­ночной цене облигации, купонной ставке, номинале и числе лет до погашения, то формула (4.2) может быть разрешена относительно показателя k_d, который и будет характеризовать искомую общую доходность YTM.4 Таким образом, пока­затель YTM численно равен такому значению ставки дисконта, который урав­нивает прогнозируемый денежный поток с текущей ценой облигации. Значение YTM может быть легко рассчитано с помощью финансового калькулятора или метода последовательных приближений.

Для примера рассчитаем доходность облигации, которая продается по но­миналу 1000 дол. и будет погашена через 20 лет. Выплата процентов осуще­ствляется каждые полгода по ставке 12% годовых:5

Для определения показателя YTM, равного k_d из этого уравнения, проще всего воспользоваться специализированным калькулятором. Ответ будет k_d = 12%.6

Доходность к погашению облигации, продаваемой по номиналу, складыва­ется исключительно за счет купонных выплат. Однако, если облигация прода­ется по цене, отличной от номинала, на величину доходности оказывают вли­яние как купонные платежи, так и капитализированный доход (или убыток). Таким образом, доходность облигации без права ее досрочного погашения в зна­чительной степени зависит от ее текущей цены. Поскольку цена покупки обли­гаций постоянно меняется в зависимости от изменения процентных ставок по аналогичным финансовым инструментам, не остается постоянной и доходность облигаций.

Доходность облигации на момент отзыва с рынка

Если облигация эмитирована на условиях возможного ее досрочного отзыва с рынка ценных бумаг, так называемая отзывная облигация, то в случае peaлизации этого права эмитентом держатель облигации обязан предъявить ее для погашения досрочно. Причины могут быть разные. Например, фирма эмитировала отзывные 12%-ные облигации номиналом в 1000 дол. В случае падения процентных ставок с 12 до 8% более выгодно для компании погасить 12%-ные облигации, заменив их 8%-ными облигациями нового выпуска и сэкономив на этом 1000 дол.(0.12-0.08) = 40 дол. на облигацию в год. Технология подобных решений будет подробно рассмотрена в главе 15. Как же повлияет эта операция на ожидаемую доходность облигации?

Если текущая процентная ставка много ниже купонной ставки облигации, то облигация, скорее всего, будет выкуплена эмитентом. В этом случае инвесторы должны оценивать ожидаемую доходность облигации как доходность на момент отзыва (Yield to Call, YTC), а не как общую доходность. Для расчета показателя YTC необходимо изменить формулу (4.2). Определяющим являются выкупная цена и число периодов до выкупа, а не номинальная цена и число периодов до наступления срока погашения. В результате получаем

(4.3)

где V — текущая рыночная цена; m — число лет до выкупа (предполагаемого) облигации; Р_с - выкупная цена, т. е. цена, которую компания должна заплатить в случае досрочного погашения облигации (обычно она равна номиналу плюс сумма процентов за год); k_d — доходность на момент отзыва облигации (доходность досрочного погашения).

Например, если 12%-ные облигации из приведенного выше примера предполагаются к досрочному погашению через пять лет по цене 1120 дол., доходность YTC равна 13.75% и находится следующим образом:

Хотя на первый взгляд может показаться, что инвестор выигрывает в случае Досрочного выкупа, это не совсем верно. Инвестор, который имел 120 дол. в год в виде купонного дохода, получит теперь при досрочном погашении полную сумму — 1120 дол., которая может быть реинвестирована в новые облигации на оставшиеся 15 лет по текущей ставке процента — 8%. Поэтому годовой денежный поток снизится с 0.12 • 1000 дол. = 120 дол. до 0.08 • 1120 дол. = 89.60 дол. Таким образом, годовой доход инвестора уменьшится на 120 дол. — 89.60 дол. = 30.40 дол.; кроме того, по истечении 15 лет инвестор получит 1120 дол. (а не 1000 дол.). Дисконтированная цена потерь от этой операции (неполученный доход), равная примерно 260 дол., превышает дисконтированную цену премии за досрочное погашение, равную 38 дол.

В подобных ситуациях может предусматриваться и другой вариант: в течение первых пяти лет инвестор получает доход по ставке 13 75% после чего купонная ставка снижается до 8%. Легко показать, что и при такой схеме начисления процентов доходность облигации в расчете на весь 20-летний период будет ниже объявленной изначально купонной ставки 12% Ниже приведены схема денежного потока и формула для расчета доходности в этом случае:

С помощью финансового калькулятора и техники расчета показателя IRR находим ожидаемую доходность — 10.55%.7 Таким образом, в случае досрочного погашения облигации ожидаемая доходность инвестора за полный период вла­дения ею снизится с 12 до 10.55%, или на 1.45%.

Фактор налогообложения доходов инвесторов

Доходы любого инвестора подлежат налогообложению. Поэтому очевидно, что и в случае с ценными бумагами релевантными являются денежный поток и доходность, рассчитанные по данным, очищенным от налогов. Эта мысль важна потому, что, анализируя альтернативные варианты инвестиций, инвестор дол­жен иметь в виду, что различные виды доходов по-разному облагаются налогом.

Для иллюстрации вновь рассмотрим прежний пример с 12%-ными облига­циями. Если не предусматривается досрочного погашения облигации, а доход инвестора облагается налогом по ставке 28%, то доходность облигации, рассчи­танная по данным за вычетом налогов (k_dAT). может быть найдена по следующей схеме:

Решив это уравнение относительно находим, что = 8.64%. Таким образом, налогообложение значительно снижает уровень доходности.8

Несколько замечаний

Завершая описание общего подхода к оценке облигаций, необходимо сделать несколько замечаний.

Существование других моделей оценки. В этой главе не ставилась задача описать все возможные модели оценки. Используя изложенный подход, читатель при необходимости сможет самостоятельно составить модель оценки для облигации произвольного типа. В главе 15 будут рассмотрены методы оценки облигаций с нулевым купоном, в главе 16 — конвертируемых облигаций.

Защита от досрочного погашения. Выше было показано, что облигации с опционом досрочного погашения менее предпочтительны по сравнению с обычными облигациями. Вероятность объявления о досрочном погашении облигаций одинаково велика как в случае значительного снижения процентных ставок по аналогичным финансовым инструментам, так и при продаже подобных облигаций с премией. Заметим также, что в случае роста процентных ставок отзывные облигации нередко продаются с дисконтом; как правило, вероятность досрочного погашения таких облигаций незначительна — эмитент, имея право на досрочное погашение, не воспользуется им. Все участники рынка знают об этом. Именно ввиду своей определенной защищенности от досрочного погаше­ния отзывные дисконтные облигации обычно продаются по ценам, обеспечиваю­щим несколько меньшую доходность по сравнению с отзывными премиальными облигациями.

Эффективная годовая ставка. Выше был использован простейший алго­ритм расчета показателя YTM путем деления годовой ставки пополам. Это справедливо, если в расчете используется ставка, называемая специалистами с Уолл-стрит номинальной, или котируемой YTM (nominal, or quoted, YTM). Делая свой выбор, инвесторы сравнивают доходность различных облигаций; по­скольку в большинстве случаев проценты начисляются каждые полгода, такое сравнение возможно.

Проблема возникает, если сравнивается доходность YTM облигаций с раз­личной частотой начисления процентов — годовое, квартальное, ежемесячное и т. д. В этом случае необходимо перейти от номинальной ставки, , к эффек­тивной, :

(4.4)

где — номинальная годовая процентная ставка (доходность); m — коли­чество начислений процентов за год. Заметим, что /m представляет собой доходность базового периода, например k_d/2 в примере с облигацией с полуго­довым начислением процентов.

Применяя (4.4) к облигациям с полугодовым начислением процентов и но­минальной ставкой годового дохода 12%, находим

Таким образом, эффективная годовая ставка на 0.36% выше номинальной.9

Время первого платежа. Обсуждение моделей оценки облигаций предпо­лагало в неявной форме, что первая выплата процентов состоится точно через шесть месяцев после приобретения облигации. Эта предпосылка верна в основ­ном лишь в случае покупки облигаций в ходе первичной эмиссии. Для оценки облигаций, приобретаемых в произвольно выбранные моменты, модель должна быть модифицирована. Такое уточнение важно для конкретного инвестора, но не имеет принципиального значения для целей и техники финансового менедж­мента. Многие финансовые калькуляторы позволяют легко выполнять подоб­ную модификацию модели оценки.

Оценка облигаций с позиции администрации корпораций. Рассмотренные модели строились исходя из логики рассуждения рядового инвестора. Суще­ствует и другой аспект оценки — цена капитала фирмы-эмитента. Поэтому обсуждение методов оценки будет продолжено в главе 6 с учетом расходов по выпуску ценных бумаг и налогообложения корпораций.

Вопросы для самопроверки

Как оцениваются облигации?

В чем разница между доходностью облигаций, погашаемых досрочно и в обычном порядке?

Объясните разницу между номинальной доходностью облигаций и эффективной годовой процентной ставкой. Приведите пример использования этих показателей.

Оценка привилегированных акций

Привилегированные акции предполагают выплату дивиденда, обычно по фиксированной ставке, в течение неопределенного или, что имеет место чаще, в течение ограниченного временного периода. Бессрочная акция генерирует денежный поток неопределенно долго, а формула (4.1) для расчета ее оценки может быть преобразована следующим образом:

Используя другие обозначения, перепишем эту формулу:10

(4.5)

где Р₀ — текущая цена привилегированной акции; D — ожидаемый фиксированный дивиденд; k_p — текущая требуемая доходность. Так, привилегированная акция с годовым дивидендом в размере 2 дол. при требуемой на рынке доходности 10% годовых будет продаваться по цене 20 дол.:

Чаще всего дивиденды выплачиваются ежеквартально, поэтому в расчетах могут использоваться квартальные оценки: Р₀ = 0.5 дол.: 0.025 = 20.00 дол.

С помощью формулы (4.5) можно вычислять ожидаемую доходность привелегированной акции, :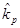

(4.5а)

Обратите внимание, что в формулах (4.5) и (4.5а) используются разные виды доходности — требуемая и ожидаемая.11 В условиях равновесного рынка обычно = .

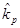В примере с привилегированной акцией, продаваемой за 20.00 дол., фор­мула (4.5а) может быть использована для нахождения ожидаемой доходности:

Это номинальная ожидаемая доходность. Чтобы найти эффективную годовую доходность, необходимо рассчитать квартальную доходность, :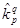

Далее, используя (4.4), находим

Если бы мы сравнивали значения доходности двух привилегированных акций с квартальным и полугодовым начислениями дивидендов, как раз и нужно было бы использовать эффективную годовую доходность.

Фактор налогообложения доходов инвестора

Выше обсуждалось влияние этого фактора применительно к облигациям. Если предположить, что банковские процентные ставки останутся неизмен­ными, можно рассчитать с помощью приведенных формул ожидаемый доход по бессрочной акции.12 Поскольку получаемые дивиденды облагаются налогом по ставке Т, доходность акции, рассчитываемая по прибыли, остающейся у ее владельца после уплаты налога, , исчисляется по формуле13

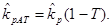(4.6)

Так, при Т = 28% и 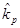=10% номинальная доходность с учетом налогообложе­ния составит

Доходность акций с позиции юридических лиц

В отличие от физических лиц дивиденды по акциям, получаемые юридиче­скими лицами, облагаются налогом по пониженной ставке — 30% ставки налога на прибыль корпораций, а соответствующая доходность находится по формуле14

(4.6а)

Так, если прибыль корпорации облагается налогом по ставке 34%, доходность 10%-ных привилегированных акций после выплаты налога составит

Таким образом, с учетом налогообложения владение привилегированными акциями более выгодно для юридических лиц по сравнению с физическими. Не случайно большинство неконвертируемых привилегированных акций в США находится во владении корпораций, а не частных лиц.

Несколько замечаний

Прежде чем перейти к обсуждению методов оценки обыкновенных акций, сделаем несколько замечаний. 1. Привилегированные акции, как правило, а эмитируются с условием создания фонда погашения (sinking fund). В этом случае предусматривается постепенное ежегодное погашение акций — обычно в размере 2% выпуска. Максимальный срок обращения таких акций не превышает 50 лет, а средний срок погашения — 25 лет. По мере приближения срока погашения остаточная стоимость акций снижается, а их ожидаемая доходность рассчитывается по тому же алгоритму, что и для бессрочных облигаций. 2. Как и в случае с облигациями, оценка акций должна рассматриваться прежде всего с позиции изменения цены капитала фирмы-эмитента. Эта проблема будет рассмотрена в главе 6. 3. Приведенные формулы основаны на предположении, что первые дивиденды будут получены через три месяца. В случае иной схемы начисления дивидендов необходимо внести соответствующую корректировку в этот алгоритм.15 4. С некоторых пор компании начали эмитировать привилегированные акции с плавающей доходностью. Эта тема будет обсуждена в главе 16.

Вопросы для самопроверки

Как оцениваются бессрочные привилегированные акции?

Как оцениваются привилегированные акции с условием создания фонда погашения?

Кто потенциальный покупатель неконвертируемых привилегированных акций? По­чему?

Оценка обыкновенных акций

Ожидаемый денежный поток, генерируемый пакетом обыкновенных акций, состоит из двух компонентов: дивидендов и выручки от возможной продажи акций. Оценка может быть выполнена с помощью различных моделей. Прежде всего, введем некоторые обозначения.

D_t — дивиденд, ожидаемый к получению в t-м году.16 D₀ обозначает по­следний фактически выплаченный дивиденд. Поскольку D_t представляет собой оценку возможных поступлений, а ожидания инвесторов и их оценки различны, значения D_t могут варьировать среди потенциальных инвесторов.

Р₀ — текущая рыночная цена акции.

— ожидаемая цена акции на конец года t. 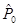— внутренняя, или теоре­тическая, стоимость (intrinsic, or theoretical, value) акции с позиции инве­стора, выполняющего анализ; — стоимость, ожидаемая на конец первого года, и т. д. Отметим, что 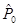представляет собой субъективную оценку инвесто­ром ожидаемого потока дивидендов и рисковость акции. Следовательно, хотя фактическая цена Р₀ фиксирована и известна всем инвесторам, 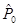может раз­личаться в их оценках в зависимости от степени оптимизма, с которым они воспринимают деятельность компании. 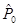может отклоняться в любую сторону от Р₀, однако очевидно, что инвестор будет покупать акции, только если по его оценке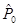 P₀. Теоретически количество оценок 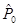может быть равно числу потенциальных инвесторов. Тем не менее можно условно говорить о не­коем маржинальном инвесторе, чьи действия фактически определяют рыночную цену. Для маржинального инвестора 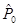= P₀, поскольку в противном случае рынок акций будет пребывать в состоянии неустойчивости, а вызванные этим дисбалансом операции по купле-продаже акций с неизбежностью приведут к установлению равновесной цены.

— предполагаемый темп прироста дивиденда в году t. Значение этого показателя может варьировать среди инвесторов, а его динамика — подчиняться некоторой закономерности. Если = , т. е. темп прироста постоянен во времени, акция называется постоянно растущей (constant growth) акцией.

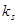— требуемая доходность акции, учитывающая как риск, так и доход­ность альтернативных вариантов инвестирования. Показатель варьирует среди инвесторов в зависимости от их оценки степени риска компании-эмитента.

— ожидаемая доходность. Ее значение может варьировать среди инвесто­ров при условии равновесного рынка этих акций для маржинального инвестора ( = ).

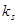Базовая формула (4.1) может быть использована для оценки любых первичных финансовых активов. Так, при покупке пакета акций на неопределенно долгое время с целью получения дивидендов теоретическая стоимость акции, 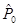, равна дисконтированной стоимости ожидаемого потока дивидендов:

(4.7)

С практической точки зрения бесконечный поток можно заменить на конечный, поскольку вкладом слагаемых с порядковыми номерами, превышающими 40, можно пренебречь ввиду его незначительности.

Как же исчисляется стоимость акции, если инвестор планирует владеть ею лишь ограниченный промежуток времени, скажем пять лет, а затем продать ее? Оказывается, используется та же самая формула (4.7). Для того чтобы убедиться в этом, представьте себя на месте очередного покупателя — он оценит акцию исходя из ожидаемого денежного потока плюс цена возможной реализации. Третий покупатель, приобретая акцию, вновь будет ориентиров на величину ожидаемых дивидендов и цену возможной реализации. Продолжая этот процесс до бесконечности, видим, что теоретическая стоимость акции определяется лишь величиной прогнозируемого потока дивидендов.

Формула (4.7) представляет собой обобщенную модель оценки акций в том смысле, что число периодов, в течение которых поступают дивиденды, может быть любым. Тем не менее есть много причин рассматривать ограниченный промежуток времени и в дальнейшем в случае необходимости переходить от упрощенной модели к модели общего вида. Некоторые частные модели оценки будут рассмотрены ниже.

Постоянный рост

Если предполагается, что дивиденды по акциям будут неопределенно долго расти с постоянным темпом прироста, т. е. = , при любом t, формула (4.7) может быть приведена к следующему виду:17

(4.8)

Модель оценки акций с равномерно возрастающими дивидендами, выраженная (4.8), часто называют моделью Гордона по имени Майрона Дж. Гордона, который много сделал для ее развития и популяризации.

В том случае, если =0, модель Гордона трансформируется в уже извест­ную модель, описываемую формулой (4.5). Очевидно также, что модель Гордона имеет смысл лишь при 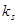> g.

Рассмотрим пример, иллюстрирующий применение модели Гордона и кон­цепции линии рынка ценных бумаг (SML). Предположим, что корпорация «McLaughlin Foods» только что выплатила дивиденды в размере 2.00 дол. (т. е. J DO = 2.00 дол.); инвестор ожидает, что дивиденды будут увеличиваться с по-стоянным темпом прироста 6%, β-коэффициент акций равен 1.2; безрисковая доходность — 8%; доходность рынка в среднем — 14%. Предполагая, что SML адекватно описывает взаимосвязь риска и доходности, можно рассчитать требу­емую инвестором доходность акций корпорации «McLaughlin»:

По формуле (4.8)

Итак, теоретическая стоимость акции с позиции данного инвестора равна 23.04 дол. Если на рынке эти акции продаются по более низкой цене, инве­стор приобретает их.

Другие инвесторы действуют по такому же алгоритму. Конечно, многие инвесторы пользуются услугами таких консультационных фирм, как «Merrill Lynch» и «Paine Webber», тем не менее алгоритмы оценки остаются теми же самыми. Если инвесторы полагают, что теоретическая стоимость акции пре­вышает текущую рыночную цену, спрос на нее увеличивается, что приводит к выравниванию этих показателей. Если текущая цена завышена, происходит обратное. Равенство цен как раз и означает равновесие рынка данных акций. Как только равновесие достигнуто — и это обычная ситуация — цена акции будет относительно стабильной, объем сделок с данной ценной бумагой — срав­нительно небольшим; это будет продолжаться до тех пор, пока на рынок не поступит новая информация, например сообщение о планируемом повышении доходов компании.

Формулу (4.8) можно переписать иначе:

(4.9)

Эта формула может быть использована для исчисления ожидаемой доходно­сти. В условиях равновесного рынка для маржинального инвестора Р₀ = 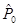и = 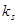. Из (4.9) видно, что ожидаемая общая доходность равна сумме ожи­даемой дивидендной доходности и темпа прироста дивидендов. Кроме того, по­казатель д может быть интерпретирован как доходность капитализированной прибыли (капитализированная доходность). Таким образом, делая допущение о стабильном росте характеристик акции, инвесторы предполагают, что доходы компании, выплачиваемые дивиденды и соответственно цена акции изменяются с одним и тем же темпом g. Отсюда следует, что если Р и D меняются одинаково, то отношение будет оставаться постоянным при любом значении t.

Оценка целесообразности капитализации прибыли

Определенную сложность представляет собой оценка акционерами целесообразности капитализации (реинвестирования) части прибыли. Представим формулу (4.8) в несколько ином виде (обоснование некоторых условий этого представления будет дано в главе 6):

(4.8а)

где EPS₁ — ожидаемый доход (чистая прибыль) на одну акцию, PR — доля прибыли, выплаченная в виде дивидендов (payout ratio); RR — коэффициент реинвестирования прибыли (retention ratio); ROE — рентабельность собственного капитала.

Теперь рассмотрим четыре различные ситуации.

1. Предположим, что фирма выплачивает всю прибыль в виде дивидендов. В этой ситуации доходы фирмы генерируются имеющимися активами и приобретения новых активов не предвидится. Амортизационные отчисления используются лишь для возмещения выбывающих основных средств; следовательно, рентабельность деятельности фирмы остается неизменной на протяжении всех лет. В частности, представим себе компанию со следующими характеристиками: PR = 1, RR = 1 - PR = 0, EPS₁ = EPS₂ = =EPS_∞ = 1 дол., k_s = 15%. Тогда стоимость акции фирмы

2. Допустим, что лишь половина прибыли выплачивается в виде дивидендов, а оставшаяся часть расходуется на финансирование новых проектов, обеспечивающих ROE = 15%. Несмотря на то, что экономический потенциал фирмы увеличивается, стоимость акции остается неизменной:

3. Предположим, что невыплаченная прибыль инвестируется в проекты с ROE = 20%. В этом случае стоимость акции фирмы возрастет:

4. При инвестировании прибыли в менее рентабельные проекты (I = 10%) стоимость акции фирмы упадет:

Приведенные примеры позволяют сделать очень важный вывод: реинвестированная прибыль оказывает позитивное влияние на стоимость акции фирмы только в том случае, если рентабельность инвестиций превышает требуемую рентабельность собственного капитала. Потенциал фирмы может увеличиваться за счет реинвестирования прибыли в проекты с ROE ≤ k_s, однако акционеры выигрывают лишь в том случае, если прибыль реинвестируется в проекты с по­ложительным NPV; экспансия в размерах необязательно выгодна акционерам.

Непостоянный рост

Допущения о постоянном росте дивидендов можно сделать в отношении лишь ряда компаний; для большинства фирм оно неправомочно. Например, в отношении акций компаний, ориентирующихся на новейшие технологии, можно ожидать быстрый рост дивидендов в течение нескольких лет, затем по­следует неизбежное замедление темпов. Фирмы, испытывающие финансовые затруднения, также могут временно приостанавливать увеличение дивидендных выплат. Стоимость акций таких компаний может рассчитываться следующим образом.

1. Разделение потока дивидендов на две части — начальный период непо­стоянного роста сменяется периодом постоянного роста.

2. Нахождение приведенной стоимости потока дивидендов, ожидаемых в период непостоянного роста.

3. Использование модели постоянного роста для нахождения ожидаемой сто­имости акции к началу периода постоянного роста, а затем дисконтирование этой величины к текущему моменту.

4. Суммирование этих двух оценок для нахождения теоретической стоимо­сти акции:

(4.10)

где n — ожидаемое число лет непостоянного роста; D_t — ожидаемый дивиденд в году t фазы непостоянного роста; D_n+1 — первый ожидаемый дивиденд фазы постоянного роста; k_s — требуемая доходность акции; g — ожидаемый темп прироста, когда компания достигает стабильности.

В качестве примера рассмотрим данные о компании «Solar Laser Technolo­gy» (SLT): n = 3; D₀ =1.82 дол.; k_s =16%; g_t = 30% в течение года трехлетнего периода быстрого роста; g = 10%.

Шаг 1. Разделим поток дивидендов SLT на две части: поступления в течение трехлетнего периода и дивиденды в последующие периоды.

Шаг 2. Находим приведенную стоимость ожидаемых дивидендов на первом этапе, :

Шаг 3. Находим ожидаемую стоимость акции SLT к началу фазы постоян­ного роста, , затем дисконтируем ее, чтобы рассчитать приведенную стоимость :

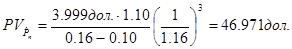
Рис. 4.1. Непостоянный рост («Solar Laser Technology»).

Шаг 4. Находим теоретическую стоимость акции:

На рис. 4.1 приведена графическая интерпретация изложенного алгоритма. Графическое представление особенно удобно в том случае, когда темп прироста варьирует, прежде чем выйти на стабильный уровень.

Рассмотренная модель называется двухуровневой моделью. В случае необходимости можно составить модель более высокого уровня. Также отметим, что многие начинающие компании изначально не платят дивидендов. Тем не менее следует иметь в виду, что при выходе на определенный уровень производства компания все же начнет выплачивать дивиденды. «Hewlett—Packard», IBМ и многие другие компании не платили дивидендов в начале своей деятельности, но платят их сегодня. «Genentech», крупнейшая компания в области биотехнологий, в настоящее время не платит дивидендов, тем не менее, инвесторы ожидают грядущих выплат в некотором будущем.

Для компании с D₀ = 0 дол. формулу (4.10) целесообразно представит в виде трех слагаемых:

(4.10а)

Первое слагаемое показывает, что дивиденды не будут выплачиваться на протяжении L лет. Второе слагаемое подразумевает, что дивиденды впервые будут выплачены в году L + 1, а далее до момента М они будут расти с переменным темпом. Третье слагаемое характеризует ту часть приведенной стоимости акции, которая будет обеспечена при выходе компании на стабильный уровень производства и выплаты дивидендов.

Фактор налогообложения доходов инвесторов

Выше отмечалось, что для инвестора релевантными являются денежный поток, построенный с учетом выплаты налогов, и доходность, исчисленная на посленалоговой базе.

Постоянный рост. Напомним, что в этом случае ожидаемая доходность акций, , складывается из постоянной дивидендной доходности и доходно­сти капитализированной прибыли. Значение этих показателей нужно скор­ректировать на величину налогов. Предположим, что индивидуальный инве­стор, облагаемый налогом на доходы по ставке 28%, анализирует целесообраз­ность покупки акций одной из двух компаний: высокодоходной компании с Р₀ = 30 дол., D₁ = 3.60 дол. и g = 3% или быстрорастущей компании с Р₀ = 30 дол., D₁ = 0.90 дол. и g = 12%. Планируется по истечении года про­дать купленные акции. Какова ожидаемая доходность акций до и после уплаты налогов?

Поиск по сайту: