 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Нормальное распределение. Нормальное распределение, хорошо описывающее многие практические ситуации, широко распространено на практике
Нормальное распределение, хорошо описывающее многие практические ситуации, широко распространено на практике. Плотность распределения вероятностей симметрична относительно ожидаемой величины и имеет область определения от — ∞ до +∞. На рис. 2А.3 представлена кривая нормального распределения со средней доходностью,  , 10% и средним квадратическим отклонением,
, 10% и средним квадратическим отклонением, 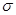 , равным 5%. Любое нормальное распределение обладает следующим свойством: площадь фигуры, ограниченной осью абсцисс, графиком плотности распределения и прямыми, пересекающими ось абсцисс в точках
, равным 5%. Любое нормальное распределение обладает следующим свойством: площадь фигуры, ограниченной осью абсцисс, графиком плотности распределения и прямыми, пересекающими ось абсцисс в точках  ±
± 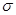 , составляет 68.3%, общей площади, лежащей между графиком плотности и осью абсцисс; если прямые проходят через точки
, составляет 68.3%, общей площади, лежащей между графиком плотности и осью абсцисс; если прямые проходят через точки  ± 2
± 2 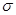 или
или  ± 3
± 3 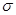 , доля площади увеличивается соответственно до 95.5 и 99.7%. Следовательно, вероятность того, что фактическая доходность будет колебаться в диапазоне от 5 до 15% (
, доля площади увеличивается соответственно до 95.5 и 99.7%. Следовательно, вероятность того, что фактическая доходность будет колебаться в диапазоне от 5 до 15% ( ±
± 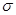 ), составляет 68.3%, и т. д. Очевидно, что чем меньше величина среднего квадратического отклонения, тем меньше вероятность слишком большого отклонения фактической доходности от ожидаемого среднего значения, а значит, и меньше общий риск инвестирования. Чтобы определить вероятность того, что результат будет меньше 7.5 и 12.5%, нужно вычислить площадь под кривой между этими точками, или заштрихованную площадь на рис. 2А.3. Эта площадь может быть определена путем интегрирования или, еще проще, с помощью статистических таблиц площади под
), составляет 68.3%, и т. д. Очевидно, что чем меньше величина среднего квадратического отклонения, тем меньше вероятность слишком большого отклонения фактической доходности от ожидаемого среднего значения, а значит, и меньше общий риск инвестирования. Чтобы определить вероятность того, что результат будет меньше 7.5 и 12.5%, нужно вычислить площадь под кривой между этими точками, или заштрихованную площадь на рис. 2А.3. Эта площадь может быть определена путем интегрирования или, еще проще, с помощью статистических таблиц площади под

|
кривой нормального распределения.3 Эти таблицы построены для стандартизованного нормального распределения, т. е. распределения нормированной величины z:4
 (2А.1)
(2А.1)
где х — значение доходности.
Для того чтобы определить вероятность варьирования доходности в интервале от 7.5 до 12.5%, найдем значения z в этих точках по формуле (2А.1):

Из табл. 2А.1 находим, что площадь фигуры, ограниченной прямыми, пересекающими ось абсцисс в точках  и z при |z| = 0.5, равна 0.1915. Это означает, что вероятность получения доходности в размере от 7.5 до 10% (или от 10 до 12.5%) равна 0.1915, или 19.15%:5 Таким образом, вероятность колебания доходности от 7.5 до 12.5% составляет 38.3%.
и z при |z| = 0.5, равна 0.1915. Это означает, что вероятность получения доходности в размере от 7.5 до 10% (или от 10 до 12.5%) равна 0.1915, или 19.15%:5 Таким образом, вероятность колебания доходности от 7.5 до 12.5% составляет 38.3%.
Предположим, нужно найти вероятность того, что фактическая доходность будет ниже нуля. Из табл. 2А.1 находим, что вероятность варьирования доходности от 0 до 10% равна 0.4773. В силу симметричности распределения вероятность того, что доходность будет меньше среднего значения, равна 0.5. Следовательно, значение фактической доходности может быть отрицательным с вероятностью 0.0227, или 2.27%.

|
Таблица 2A.1 Участок под кривой нормального распределения
| Z | Площадь, ограниченная прямыми, проходящими через точки  и х и х
|
| 0.0 | 0.0000 |
| 0.5 | 0.1915 |
| 1.0 | 0.3413 |
| 1.5 | 0.4332 |
| 2.0 | 0.4773 |
| 2.5 | 0.4938 |
| 3.0 | 0.4987 |
Примечание. Здесь z означает число средних квадратических отклонений заданного значения х от центра распределения. Некоторые таблицы составляют таким образом, чтобы показать площадь фигуры, лежащей слева или справа от указанного значения z; в этой таблице приведена площадь фигуры, ограниченной прямыми, проходящими через z и центр распределения. Таким образом, участок между центром распределения и точкой, где z равно +0.5 или —0.5, составляет 0.1915, т. е. 19.15% общей площади или вероятности. Более полный ряд значений площади приведен в табл. 1.5 в конце книги.
Поиск по сайту: