 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Линия рынка ценных бумаг
Следующим шагом в понимании логики САРМ является переход от риска и доходности эффективных портфелей к риску и доходности отдельных ценных бумаг. В теории САРМ рисковость ценной бумаги измеряется ее β -коэффициентом (подробно рассматривается ниже). β -коэффициент характеризует изменчивость доходности акции относительно доходности рынка ценных бумаг. По определению, некая «средняя» акция имеет β, равную 1.0; акция, изменчивость доходности которой выше, чем в среднем на рынке, имеет β, превышающую 1.0; а акция с изменчивостью доходности ниже рыночной имеет β, меньшую 1.0. Уравнение, устанавливающее связь между риском акции, измеряемым β, и доходностью акции, называется уравнением линии рынка ценных бумаг (Security Market Line, SML):
(3.2)
где ki — требуемая доходность i-й акции (ранее мы определили 
как ожидаемую доходность; при условии равновесия рынка 
); 
— безрисковая доходность, в качестве которой обычно принимается доходность облигаций казначейства США;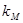 
— требуемая доходность портфеля, состоящего из всех акций, или рыночного портфеля. На рынке, находящемся в состоянии равновесия, требуемые значения доходности должны равняться ожидаемым, т. е. = 
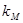заметим, что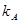 
— требуемая доходность средней акции в рыночном портфеле;6 таким образом, 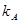= 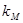; 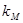— = RPM — рыночная премия за риск, или цена риска, для средней акции; это дополнительная доходность, превышающая безрисковую доходность, которая требуется, чтобы компенсировать инвесторам принимаемую ими среднюю величину риска; βi — β -коэффициент i-й акции; (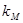 — ) βi = RP i — премия за риск владения i -й акцией. Этот показатель варьирует в зависимости от того, является данная акция более или менее рисковой по сравнению с другими, т. е. имеющей большее или меньшее значение β.
Следовательно, если = 9%, 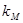= 13% и βi = 0.5, то, согласно формуле (3.2), k i = 11%:
k i = 9% + (13% - 9%)0.5 = 11%.
На рис. 3.3 изображена SML, у которой = 9% и 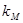= 13%. Необходимо отметить следующее.
1. Значения требуемой доходности показаны на вертикальной оси, а риска, измеряемого с помощью β -коэффициента, — на горизонтальной.
2. Безрисковые ценные бумаги имеют βi = 0; поэтому соответствует пересечению SML с вертикальной осью.
3. Наклон SML (в нашем примере 
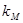= ( — )/(l.0 — 0.0) = 13% — 9% = 4%) характеризует склонность к риску в данной экономике: чем больше склонность к риску среднего инвестора, тем, во-первых, круче наклон SML, во-вторых, больше премия за риск для любого рискового актива, в-третьих, выше требуемая доходность на рынке в целом. Заметим, что крутизна линии SML определяется не β -коэффициентом, исчисляемым по специальному алгоритму, который будет изложен ниже, а рыночной премией за риск; в ситуации, представленной на рис. 3.3, она равна 4% на каждую единицу прироста β.
4. Значения требуемой доходности и премии за риск показаны для акций с βi = 0.5, βi = 1.0 и βi = 2.0.
Как следует из уравнения SML, требуемая доходность зависит не только от рыночного риска, измеряемого ß, но и от безрисковой ставки и премии за рыночный риск. С изменением этих переменных меняется и SML.
Поиск по сайту: