 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Портфель, оптимальный с точки зрения инвестора
На рис. 2.10, так же как и на рис. 2.6, приводится допустимое множество портфелей, состоящих из двух активов, в предположении, что r A,B = 0. Оптимальный

портфель с точки зрения отдельного инвестора — это точка пересечения эффективного множества портфелей и одной из кривых безразличия и инвестора. Эта точка пересечения соответствует наиболее высокому уровню удовлетворенности, которого может достичь инвестор. М-с Y, которая менее склонна к риску, чем м-р Z, выбирает портфель с более низкой ожидаемой доходностью (около 6%) и уровнем риска, равным 4.2%. М-р Z выбирает портфель, ожидаемая доходность которого составляет около 7.2%, однако уровень риска этого портфеля примерно равен 7.1%. Доля ценных бумаг, имеющих низкий уровень риска, в портфеле м-с Y является достаточно высокой, тогда как портель м-ра Z характеризуется большим удельным весом высокорисковых ценных бумаг.14
Вопросы для самопроверки
Что такое эффективная граница?
Что такое кривые безразличия?
Объясните, как происходит процедура выбора инвестором его оптимального портфеля.
Резюме
Основные цели этой главы состояли в том, чтобы: 1) показать, как измеряется риск отдельного актива, и 2) объяснить, какое воздействие на риск актива оказывает включение его в портфель ценных бумаг. Ниже перечислены основные понятия, которые рассматривались в этой главе.
• В целом риск можно определить как вероятность осуществления некоторого нежелательного события.
• Риск инвестиции связан с вероятностью получения доходности ниже ожидаемого уровня — чем выше возможность низкой доходности или убытка, тем более рисковой является инвестиция.
• Ожидаемая доходность инвестиции — это ожидаемое среднее значение распределения вероятностей возможных значений доходности (математическое ожидание. — Прим. ред.).
• Рациональные инвесторы владеют портфелем рисковых активов, в первую очередь учитывая риск портфеля, а не риск отдельных активов, его составляющих.
• Общий риск, количественно оцениваемый дисперсией отдельных значений доходности относительно ее среднего значения, является релевантным измерителем риска актива, рассматриваемого изолированно.
• При объединении активов в портфели релевантным является рыночный риск актива, который представляет собой долю риска данного актива в риске портфеля в целом.
• Общий риск актива можно измерить с помощью дисперсии его доходности, среднего квадратического отклонения доходности или коэффициента вариации доходности. Наиболее предпочтительной мерой в сравнительном анализе общего риска ряда активов является коэффициент вариации.
• Ожидаемая доходность портфеля представляет собой средневзвешенную доходность отдельных активов, однако среднее квадратическое отклонение портфеля не равно средневзвешенной из средних квадратических отклонений отдельных активов, его составляющих.
• Поскольку между большинством активов не существует функциональной связи, объединение активов в портфель снижает риск портфеля в целом.
• Общий риск актива включает в себя специфический для компании (диверсифицируемый) риск, который можно устранить с помощью диверсификации, и рыночный риск, который нельзя устранить диверсификацией.
• Допустимое множество портфелей включает в себя все портфели, которые можно составить исходя из данного набора активов.
• Эффективный портфель — это портфель, который обеспечивает наибольшую доходность при данном уровне риска или наименьший риск при данной доходности.
• Оптимальный для инвестора портфель определяется как точка пересечения эффективного множества портфелей с наиболее высокой кривой безразличия данного инвестора.
В следующей главе мы продолжим рассмотрение риска и доходности в направлении: 1) обсуждения безрисковых активов и их влияния на выбор инвестора, 2) нахождения статистической характеристики, которую можно использовать для измерения рыночного риска (β-коэффициент), и 3) анализа взаимосвязи между риском и ожидаемой доходностью.
Вопросы
2.1. Дайте определение следующих понятий, используя для иллюстрации ваших ответов графики и формулы в тех случаях, когда это возможно:
а) риск, распределение вероятностей;
б) ожидаемая доходность (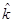 );
);
в) среднее квадратическое отклонение (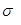 ), дисперсия (
), дисперсия (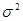 ), коэффициент вариации (CV);
), коэффициент вариации (CV);
г) общий риск;
д) рыночный риск;
е) портфель;
ж) ожидаемая доходность портфеля (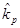 ),
),
з) коэффициент корреляции (r);
и) диверсифицируемый риск;
к) допустимое множество;
л) эффективный портфель;
м) граница эффективности;
н) кривая безразличия;
о) оптимальный портфель.
2.2. Крутизна кривой непрерывного распределения вероятностей ожидаемой доходности менее рисковых активов более резко выражена, чем крутизна кривой для более рисковых активов. Какую форму приняла бы эта кривая в случаях: а) безрисковых активов и б) активов с абсолютно непредсказуемой доходностью?
2.3. Предположим, вы обладаете портфелем, состоящим из долгосрочных государственных облигаций США на сумму 500 000 дол.
а. Будет ли ваш портфель безрисковым?
б. Теперь предположим, что вы обладаете портфелем, состоящим из 30-дневных казначейских векселей на сумму 500 000 дол. Каждые 30 дней ваши векселя подлежат погашению, и вы вновь вкладываете вырученную сумму (500 000 дол.) в новую партию векселей. Предположим, что доходы, генерируемые инвестиционным портфелем, являются вашим единственным источником существования и что вы хотите поддерживать некоторый постоянный жизненный уровень. Является ли ваш портфель действительно безрисковым?
в. Вы должны были прийти к выводу, что оба портфеля — как с долгосрочными, так и с краткосрочными государственными ценными бумагами — имеют некоторый элемент риска. Можете ли вы привести пример каких-либо абсолютно безрисковых ценных бумаг?
2.4. Полис страхования жизни — это финансовый актив. Выплачиваемые страховые взносы представляют стоимость капиталовложений.
а. Как вы рассчитаете ожидаемую доходность этого актива?
б. Предположим, что владелец страхового полиса не имеет других финансовых активов, однако обладает неким «человеческим» капиталом, т. е. способностью зарабатывать. Каков коэффициент корреляции между доходами от страхового полиса и доводами от «человеческого» капитала держателя полиса?
в. Компании по страхованию жизни должны оплачивать административные расходоы и комиссионные страховым агентам; следовательно, ожидаемая доходность страховых взносов обычно низка или даже отрицательна. С помощью принципа портфеля ценных бумаг объясните, почему люди покупают полис страхования жизни несмотря на отрицательную ожидаемую доходность?
Задачи
2.1. Ожидаемая доходность. Акции А к В имеют следующие распределения вероятностей ожидаемой доходности:
| Вероятность……………. | 0.1 | 0.2 | 0.4 | 0.2 | 0.1 |
| А, %.....…………………. | -25 | ||||
| В, %.....…………………. | -40 |
а. Подсчитайте ожидаемую доходность, 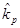 , для акции В (
, для акции В (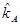 = 15%).
= 15%).
б. Подсчитайте среднее квадратическое отклонение и коэффициент вариации ожидаемой доходности акции А. (Эти величины для акции В составляют 27% и 1.59). Возможно ли, что большинство инвесторов сочтут акции В менее рисковыми, чем акции А? Объясните.
2.2. Ожидаемая доходность. Допустим, вам предложили: 1) 1 млн. дол. или 2) игру с подбрасыванием монеты, в которой можно получить 2 млн. дол., если выпадет решка, или нуль, если выпадет орел.
а. Какова ожидаемая стоимость игры?
б. Что бы вы предпочли: 1 млн. дол. или игру?
в. Если вы выберете 1 млн. дол., то относитесь ли вы к числу тех, кто избегает риска, или тех, кто его ищет?
г. Допустим, вы выберете 1 млн. дол. Вы можете вложить его или в казначейские долгосрочные облигации США, которые превратятся в 1 075 000 дол. в конце года, или в обыкновенные акции, которые с одинаковой вероятностью могут или обесцениться, или стоить 2 300 000 дол. в конце года.
• Какова ожидаемая прибыль в долларах в случае инвестирования в акции? (Ожидаемая прибыль от инвестиций в долгосрочные казначейские облигации составляет 75000 дол.).
• Какова ожидаемая доходность вложений в акции? (Ожидаемая доходность вложений в казначейские облигации составляет 7.5%).
• Вложите ли вы деньги в облигации или в акции?
• Насколько высока должна быть ожидаемая прибыль (или доходность) от вложения в акции, чтобы заставить вас купить их?
• Что предпочтительнее: купить одну акцию за 1 млн. дол. или составить портфель из 100 акций по 10 000 дол. каждая? Каждая из этих акций имеет те же характеристики доходности, что и одна акция за 1 млн., т. е. имеет одинаковый шанс или обесцениться до нуля, или принести 23 000 дол. в конце года. Имеет ли значение корреляция между доходностью этих акций?
2.3. Анализ общего риска. Корпорация «Berry» рассматривает три возможных инвестиционных проекта на следующий год. Каждый проект рассчитан на один год, а доходы от проекта зависят от состояния экономики в следующем году. Ориентировочные оценки доходности приведены ниже:
| Состояние экономики | Вероятность | Прогнозируемая доходность, % | ||
| A | B | C | ||
| Спад | 0.25 | |||
| Средний уровень | 0.50 | |||
| Процветание | 0.25 |
а. Рассчитайте ожидаемую доходность каждого проекта, дисперсию, среднее квадратическое отклонение и коэффициент вариации.
б. Проранжируйте альтернативы исходя из: 1) ожидаемой доходности, 2) риска. Какую альтернативу вы выберете?
2.4. Анализ эффекта портфеля и рыночного риска. Обратимся к трем альтернативным проектам, описанным в задаче 2.3. Допустим, что «Berry» собирается вложить треть имеющихся у нее средств в каждый проект, создав портфель из трех активов с одинаковым удельным весом.
а. Какова ожидаемая доходность портфеля?
б. Каковы дисперсия и среднее квадратическое отклонение портфеля?
в. Каковы коэффициенты ковариации и корреляции для проектов А и В? Для проектов А и С?
2.5. Фактическая доходность. По данным прошлых периодов акции А к В имели следующие дивиденды и цены (в дол.):
| Год | Акция А | Акция В | ||
| дивиденд | цена в конце года | дивиденд | цена в конце года | |
| - | 22.50 | - | 43.75 | |
| 2.00 | 16.00 | 3.40 | 35.50 | |
| 2.20 | 17.00 | 3.65 | 38.75 | |
| 2.40 | 20.25 | 3.90 | 51.75 | |
| 2.60 | 17.25 | 4.05 | 44.50 | |
| 2.95 | 18.75 | 4.25 | 45.25 |
а. Подсчитайте фактическую доходность акций за каждый год. Затем предположите, что кто-то обладает портфелем, состоящим на 50% из акций А и на 50% из акций В (структура портфеля балансировалась в конце очередного года). Рассчитайте доходность портфеля за каждый год с 1988-го по 1992-й. Какую доходность по годам обеспечивали каждый актив и портфель в целом? (Указание: фактическая доходность за любой период 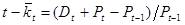 ).
).
б. Вычислите среднее квадратическое отклонение доходности каждой акции и портфеля.
(Остальные задания выполняются с помощью компьютера и электронных таблиц).
в. Добавьте акцию С к портфелю; за истекшие периоды акция С имела следующие дивиденды и цены (в дол.):
| Год | дивиденд | цена в конце года |
| - | 23.40 | |
| 1.85 | 23.90 | |
| 1.95 | 31.50 | |
| 2.05 | 27.20 | |
| 2.15 | 32.25 | |
| 2.25 | 26.00 |
Предположим, что акции А, В к С имеют равный удельный вес в портфеле (по 33.3%). Как это повлияет на доход портфеля и среднее квадратическое отклонение?
г. Произведите некоторые дополнительные изменения в процентном соотношении акций в портфеле, обеспечив при этом в сумме 100%. Например, поместите 100% капитала в акции А; 25% в А, 25% в В и 50% в С, и т. д. Объясните причины изменения величин 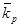 и
и 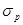 .
.
д. Предпочли бы вы иметь портфель, содержащий 1/3 каждого вида акций, или портфель, состоящий на 50% из акций А и на 50% из акций В? Объясните.
2.6. Риск портфеля. За истекшие периоды акции А и В имели следующие дивиденды и цены (в дол.):
| Год | Акция А | Акция В | ||
| дивиденд | цена в конце года | дивиденд | цена в конце года | |
| - | 12.25 | - | 22.00 | |
| 1.00 | 9.75 | 2.40 | 18.50 | |
| 1.05 | 11.00 | 2.60 | 19.50 | |
| 1.15 | 13.75 | 2.85 | 25.25 | |
| 1.30 | 13.25 | 3.05 | 22.50 | |
| 1.50 | 15.50 | 3.25 | 24.00 |
а. Подсчитайте фактическую доходность по годам для каждой акции. Рассмотр портфель, состоящий на 50%из акций А и на 50% из акций В. (Портфель балан руется каждый год с целью поддержания данного процентного соотношения). Как доходность портфеля по годам с 1988 по 1992 г.? Каков средний доход для каждой ции и для всего портфеля? (Указание: фактическая доходность за любой период  .
.
б. Рассчитайте среднее квадратическое отклонение доходов для каждой акции и всего портфеля.
в. Основываясь на том, что риск портфеля меньше, чем риск составляющих его активов, рассматриваемых индивидуально, можете ли вы предположить, к какой величине ближе коэффициент корреляции между доходностью акций — к + 0.9 или —0.9?
г. Если на основе случайной выборки увеличить число наименований акций в портфеле, то каким будет наиболее точный ответ относительно изменения величины 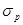 ?
?
• останется неизменной;
• будет близка к 15%;
• будет близка к нулю в случае достаточно большой добавки акций.
Поиск по сайту: