Линия рынка капитала

На рис. 2.10 изображена совокупность возможных портфелей в случае двух активов. Он демонстрирует, как могут быть использованы кривые безразли­чия для выбора оптимального портфеля из возможного множества. На рис. 3.1 построен подобный график для случая большего числа активов, а кроме того, добавлен безрисковый актив с доходностью . Безрисковый актив, по опреде­лению, имеет нулевой риск, и, следовательно, 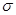= 0%, поэтому он может быть изображен точкой на вертикальной оси.

Рис. 3.1 показывает возможное множество рисковых активов (заштрихо­ванная область) и совокупность (ряд) кривых безразличия (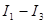), отображаю­щих выбор между риском и ожидаемой доходностью для отдельного инвестора. Точка N, в которой кривая безразличия 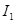является касательной к эффектив­ному множеству, отражает выбор возможного портфеля. Это точка на эффек­тивной границе множества рисковых портфелей, в которой инвестор получает самую высокую возможную доходность при данной величине риска, 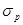, и наи­меньшую величину риска при данной ожидаемой доходности, .

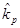Однако инвестор может сделать лучший выбор, чем портфель N; он может достичь более высокой кривой безразличия. В дополнение к возможному мно­жеству рисковых портфелей можно подключить безрисковый актив, который обеспечивает гарантированную доходность, . Имея возможность инвестировать в безрисковый актив, инвесторы могут составлять новые портфели путем включения безрискового актива в исходный портфель. Это позволяет достичь любой комбинации риска и доходности на прямой линии, соединяющей с М, точкой касания прямой линии и границы эффективного множества портфе­лей акций.3

Портфель, изображаемый точкой на линии MZ, будет предпочтительнее любого рискового портфеля, изображаемого точкой на границе эффективности BNME, поэтому точки на линии MZ представляют собой наилучшие дости­жимые комбинации риска и доходности. Имея новое множество возможностей МZ, инвестор перейдет из точки N в точку R, которая находится на бо­лее высокой достижимой кривой безразличия риск—доходность. Заметим, что любой точке на предыдущей эффективной границе BNМЕ (кроме точки каса­ния М) следует предпочесть точки, лежащие на линии МZ. Возможность перехода в некую точку R на более высоком уровне как раз и объясняется ком­бинированием безрисковой ценной бумаги и рискового портфеля М. Поскольку инвестор может получать необходимый ему кредит, а также предоставлять свои ресурсы в долг, а это эквивалентно покупке безрисковых долговых ценных бу­маг по безрисковой ставке существует возможность выхода на линейный отрезок MZ, что и происходит, если кривая безразличия инвестора касается MZ в точке М. 4

Все инвесторы при условии соблюдения предпосылок САРМ должны иметь портфели, обозначенные точками, лежащими на линии MZ, и являющие­ся комбинацией безрисковой ценной бумаги и рискового портфеля М. Таким образом, добавление безрисковой акции ведет к изменению эффективного мно­жества: оно теперь лежит вдоль линии MZ, а не вдоль кривой BNME. Также заметим, что если рынок капитала находится в равновесии, то М должно быть таким портфелем, в который любой рисковый актив включается пропорци­онально доле этого актива в общей рыночной стоимости всех активов; т. е. если доля ценной бумаги i составляет х% общей рыночной стоимости всех ценных бумаг, то х% рыночного портфеля должно приходиться на ценную бумагу i. Таким образом, все инвесторы должны владеть портфелями, изображенными точками на линии MZ, а точное расположение данного портфеля опре­деляется точкой, в которой кривая безразличия инвестора касается этой ли­нии.

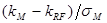Линия MZ на рис. 3.1 называется линией рынка капитала (Capital Market Line, CML). Она пересекается с вертикальной осью в точке, соответству­ющей , а ее наклон равен .5 Поэтому уравнение линии рынка капитала может быть записано следующим образом:

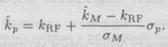
(3.1)

Уравнение (3.1) показывает, что ожидаемая доходность эффективного портфеля (т. е. портфеля, лежащего на линии CML) равна сумме безрисковой ставки и премии за риск, исчисляемой умножением ( — )/ на среднее квадратическое отклонение портфеля, 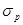. Таким образом, CML устанавливает линейную зависимость между ожидаемой доходностью и риском. Наклон CML определя­ется разностью между ожидаемой доходностью рыночного портфеля рисковых акций, , и безрисковой доходностью, (эта разность называется премией за рыночный риск), деленной на среднее квадратическое отклонение доходности рыночного портфеля, :

*

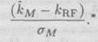Например, предположим, что = 10%, a = 15% и ам = 15%. Тогда наклон CML будет равен (15%-10%): 15% = 0.33, и если портфель имеет 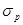= 10%, то

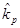= 10% + 0.33 • 10% = 13.3%.

Более рисковый портфель, 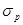= 20%, будет иметь 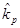= 10% + 0.33(20%) = 16.6%.

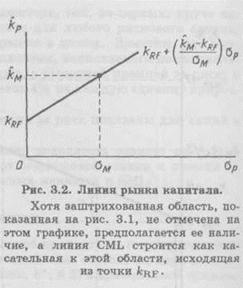
Зависимость между ожидаемой до­ходностью и риском портфеля показана графически на рис. 3.2. CML изобража­ется прямой линией, пересекающей вер­тикальную ось в точке, соответствующей значению , и имеющей наклон, рав­ный премии за рыночный риск ( — ), деленной на . Наклон CML от­ражает совокупное отношение инвесторов к риску.

Вопросы для самопроверки

Изобразите возможное множество риско­вых активов, границу эффективности и CML на одном рисунке.

Напишите уравнение CML и объясните его содержание.

Поиск по сайту: