 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Определение модели EOQ
Рис. 22.1 иллюстрирует основные предпосылки, на которых построена модель EOQ, а именно: часть затрат увеличивается с ростом объема запасов, в то время как другая часть снижается; оптимальным является размер заказа (и связанный с ним средний объем запасов), который минимизирует совокупные Утраты. Прежде всего, как было отмечено ранее, средний объем запасов зависит от частоты размещения заказов и размера каждого из них: если запасы будут обновляться ежедневно, средний объем запасов будет гораздо ниже, чем 8 случае размещения заказа один раз в год. Затем, как показано на рис. 22.1, Утраты по хранению увеличиваются с увеличением объемов заказов: большие объемы заказов означают увеличение средних запасов, а следовательно, увеличение затрат по хранению, неполученного дохода на вложенный в запасы капитал затрат на страхование и потерь от уценки. Напротив, затраты по размещению и выполнению заказов снижаются с увеличением размера партии: затраты на размещение заказов, затраты поставщиков на наладочные работы и затраты на обработку заказа уменьшаются при снижении частоты заказов, приводящей к увеличению объемов хранимых запасов.
Если сложить графики затрат по хранению запасов и выполнению заказов представленные на рис. 22.1, то их сумма будет представлять собой график общих затрат по поддержанию запасов (TIC). Точка, в которой величина TIC принимает минимальное значение, определяет оптимальный размер партии (EOQ). Продифференцировав (22.6) по Q (заказываемое количество) и приравняв результат к нулю, получаем
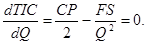
Из полученного уравнения находим величину Q:

где F — постоянные затраты по размещению и выполнению одного заказа; S — годовая потребность в запасах; С — годовые затраты по хранению, выраженные в процентах от стоимости средних запасов; Р — цена приобретения единицы запасов.
Формула (22.7) является моделью EOQ.3 Данная модель основана на следующих предположениях: 1) годовая потребность в запасах (годовой объем реализации) может быть точно спрогнозирована, 2) объемы реализации равномерно распределены в течение года, 3) не происходит задержек в получении заказов.
Поиск по сайту: