 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Основы мультипликативного дискриминантного анализа
Предположим, что управляющий банка по кредитам и займам желает разделить заявки о предоставления займов корпорациям на те, которые, вероятно, не будут выполнены, и те, которые будут выполнены. Предположим, что за некоторый прошлый период доступны данные по группе фирм, включающей как компании, которые стали банкротами, так и компании, которые не пришли к краху. Для простоты допустим, что будут проанализированы только два показателя: коэффициент текущей ликвидности (CR) и доля заемного капитала (DR). Их значения для нашей выборки фирм приведены в графах 2 и 3 в таблице к рис. 26.1. Крестиками на рисунке отмечены фирмы, ставшие банкротами, точками — фирмы, которые остались платежеспособными. Например, точка А соответствует фирме 2, имеющей CR = 3.0 и DR = 20%, банкротство ей не грозит. Точка В представляет фирму 19, CR = 1.0, DR = 60%, которая идет к банкротству.
Цель дискриминантного анализа — построение линии, делящей все компании на две группы: если точка расположена над линией, фирме, которой она соответствует, финансовые затруднения вплоть до банкротства в ближайшем будущем не грозят, и наоборот. Эта линия разграничения называется дискриминантной функцией, и в нашем примере она принимает форму линейной функцией, называемой индексом Z:
Z = а + b1CR + b2DR.
Хотя полное обсуждения дискриминантного анализа выходит далеко за пределы темы этой книги, некоторые полезные сведения могут быть получены в ходе анализа

16 Этот раздел в основном основан на работах Э. И. Альтмана, особенно на следующих статьях: Altman E. I. Financial Ratios, Discriminant Analysis, and the Prediction of Corporate Bankruptcy // Journ. Finance. 1968. Sept. P. 589-609; Altman E. I., Haldeman R. J., Narayanan P. Zeta Analysis: A New Model to Identify Bankruptcy Risk of Corporation // Journ. Banking a. Finance. 1977. June. P. 29-54.
точек графика.
1. Параметры а1, b1 и b2 дискриминантной функции рассчитываются в результате статистической обработки данных по выборке фирм, которые либо обанкротились, либо сумели выжить в течение некоторого периода. Так, по данным таблицы к рис. 26.1 с помощью компьютерной программы дискриминантного анализа можно получить следующую зависимость:
Z = - 0.3877 - 1.0736CR + 0.0579DR.
2. Эта функция изображена в виде графика на рис. 26.1 как геометрическое место точек, для которых Z = 0.17 Компаниям, расположенным выше линии (а также имеющим Z < 0), банкротство, вероятно, не грозит, тогда как компании, расположенные ниже линии (а также имеющие Z > 0), могут в будущем разориться. На графике можно увидеть, что наблюдается только три отклонения от сформированной зависимости, когда месторасположение точки не соответствует сделанным выводам. Таким образом, дискриминантный анализ продемонстрировал приемлемый способ классификации группы компаний, если не принимать во внимание три из них.
3. С помощью дискриминантной функции можно подсчитывать значение Z для других компаний, скажем, заемщиков капитала в банках. Для наших гипотетических компаний значения Z вместе с вероятностью банкротства приведены в графах 5 и 6 таблицы к рис. 26.1. Чем выше значение Z, тем хуже выглядят компании с позиции возможного банкротства. Можно дать такую интерпретацию.
Z = 0. Вероятность наступления банкротства в будущем (скажем, в течение двух лет) 50%. Значения Z таких компаний расположены прямо на линии разграничения.
Z < 0. Вероятность наступления банкротства меньше 50%. Чем меньше Z, тем благоприятнее текущее финансовое положение. Значения вероятностей, показанные в графе 6 таблицы к рис. 26.1, получены в результате применения программы MDA.
Z > 0. Вероятность наступления банкротства больше, чем 50%, и с ростом Z она увеличивается.
4. Среднее Z для компаний, которым не грозит банкротство, равно —0.583, а для потенциальных банкротов — +0.648. Можно интерпретировать рис. 26.2 следующим образом: если Z < —0.3, вероятность того, что фирма будет двигаться к банкротству, очень мала, тогда как, если Z > 0.3, существует небольшая вероятность того, что она останется платежеспособной. Если Z находится в интервале [-0.3, +0.3], который называется зоной неведения, то определенного мнения о фирме высказать нельзя.
5. Знаки параметров дискриминантной функции имеют определенный смысл. Когда этот коэффициент отрицателен, то чем больше CR, тем меньше Z этой компании, т. е. ниже вероятность неудачи. Подобным образом высокая доля заемного капитала приводит к высокому значению Z, и это прямо отражается на увеличении вероятности банкротства.

17 Чтобы начертить линию, предположим, что DR равна 0% и 80%, затем найдем CR, когда Z = 0 при этих значениях DR. Например, при DR = 0 получаем
Z = -0.3877 - 1.0736CR + 0.0579 * 0 = 0,
0.3877 = -1.0736CR, CR = -0.3611.
Таким образом, в точке —0.3611 Z пересекает ординату. Аналогично при DR = 80% получим CR = 3.9533. Нанеся эти две точки и затем соединяя их, получим дискрими-нантную линию, являющуюся линией раздела между фирмами-банкротами и преуспевающими фирмами. Следует заметить, что здесь также можно использовать нелинейные дискриминантные функции.

Укажем на определенную ошибку в классификации. Фирма 8 имеет значение Z = — 0.649, поэтому МDA не предсказывает никакого банкротства, но на самом деле фирма идет к краху. Аналогично МDA предсказывает банкротство для фирм 9 и 12, хотя они далеки от этого состояния. Ниже показано расхождение между прогнозами банкротств и платежеспособности и фактических результатов:
| Z положительно (банкротство) | Z отрицательно (платежеспособность) | |
| Число фирм, идущих к банкротству |
Таким образом, возможны и ошибки при использовании этой модели для целей прогнозирования – в данном случае мы ошиблись в отношении трех фирм, что составляет 16%. Тем не менее вероятность получения правильного прогноза достаточно велика — 84%.

| Номер фирмы | CR | DB % | Факт банкротства | Индекс Z | Вероятность банкротства, % |
| 3.6 | Нет | -0.780 | 17.2 | ||
| 2(А) | 3.0 | » | -2.451 | 0.8 | |
| 3.0 | » | -0.135 | 42.0 | ||
| 3.0 | Да | 0.791 | 81.2 | ||
| 2.8 | Нет | -0.847 | 15.5 | ||
| 2.6 | Да | 0.062 | 51.5 | ||
| 2.6 | » | 0.757 | 80.2 | ||
| 2.4 | » | -0.649 | 21.1 | ||
| 2.4 | Нет | 0.509 | 71.5 | ||
| 2.2 | » | -1.129 | 9.6 | ||
| 2.0 | » | -0.220 | 38.1 | ||
| 2.0 | » | 0.244 | 60.1 | ||
| 1.8 | Да | 1.153 | 89.7 | ||
| 1.6 | Нет | -0.948 | 13.1 | ||
| 1.6 | Да | 0.441 | 68.8 | ||
| 1.2 | » | 0.871 | 83.5 | ||
| 1.0 | Нет | -0.072 | 45.0 | ||
| 1.0 | Да | 0.391 | 66.7 | ||
| 19(В) | 1.0 | » | 2.012 | 97.9 |

Рис. 26.1. Дискриминантный анализ выборки фирм на предмет банкротства.
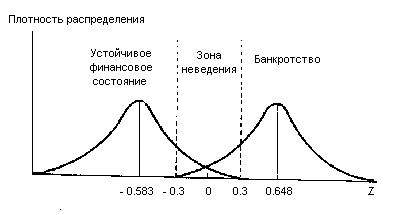
Рис. 26.2. Распределение вероятностей значений индекса Z.
6. Наша иллюстративная дискриминантная функция имеет только две переменные, но можно ввести и другие характеристики. Например, мы могли бы добавить такие переменные, как рентабельность активов, ROA, коэффициент обеспеченности процентов к уплате, TIE, оборачиваемость дебиторской задолженности в днях, DSO, коэффициент быстрой ликвидности и т. д.18 При введении в рассмотрение нового параметра, например ROA, следует рассчитать новую дискриминантную функцию:
Z = a + b1CR + b2DR + b3ROA.
Не исключено, что по новому уравнению прогноз в отношении фирм 8, 9 и 12 изменится, т. е. вполне вероятно, что добавление других характеристик улучшает точность прогнозирования банкротства. В терминах рис. 26.2 это приводит к тому, что распределение вероятностей становится более плотным (тесным), сужается зона неведения, и мы знаем более точно, как классифицировать ту или иную фирму, т. е. вероятность ошибки уменьшается.
Поиск по сайту: